条件已知两个点的坐标p1(x0,y0),p2(x1,y1)要求画出这条直线
之后的e代表每次的误差积累,初始值为0,可以计算出斜率为k=dy/dx=(y0-y1)/(x0-x1)
1、x为阶跃步长(直线光栅化) 适用于0<k<1的情况
即x每次增加1,但是y的坐标根据其是靠近该点所处的单元格的距离来决定,如果离上边近则y加1,如果离下边近则还是y
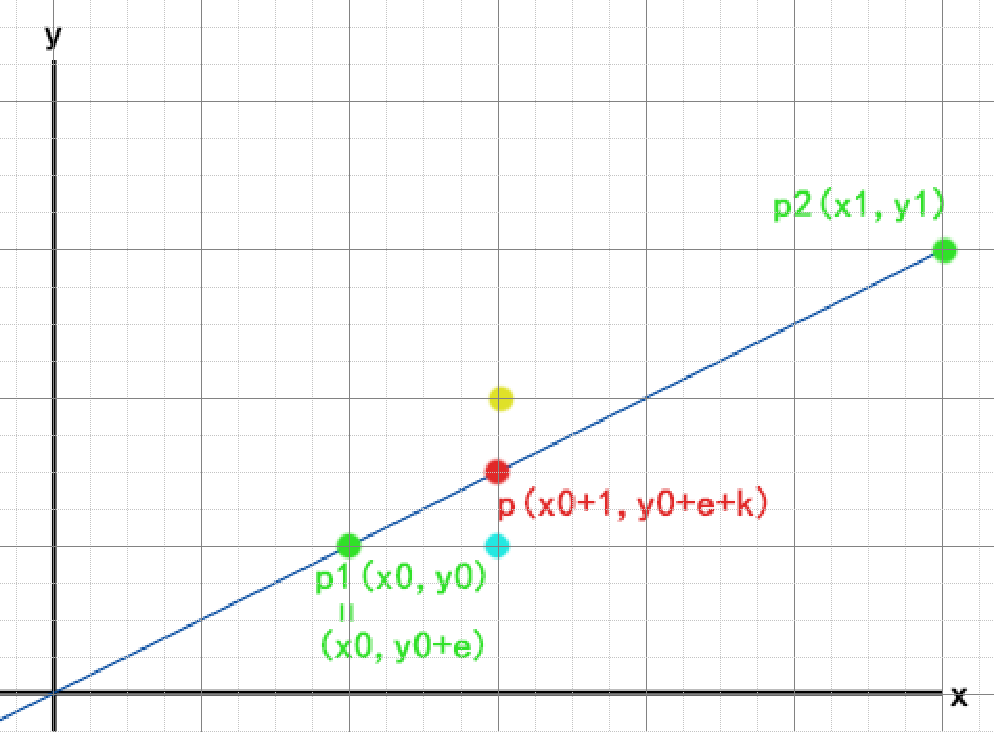
可以知道机器在画每一个点的时候都会有误差,则画出的第一个点的坐标(x0,y0)也相当于是(x0,y0+e),那么可以知道下个点的坐标为红色的p(x0+1,y0+e+k),但是机器在画p点时,如果p点的纵坐标不是整数时,应该进行判断这个点是接近黄点(x0+1,y0+1)还是接近蓝点(x0+1,y0),最后如果接近黄点则e累积k-1,如果接近蓝点则e累积k
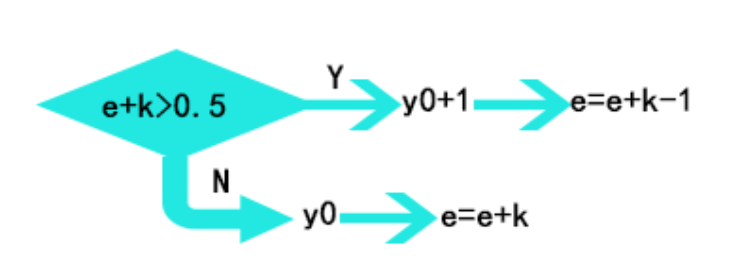
在判断条件的两边同乘2得:
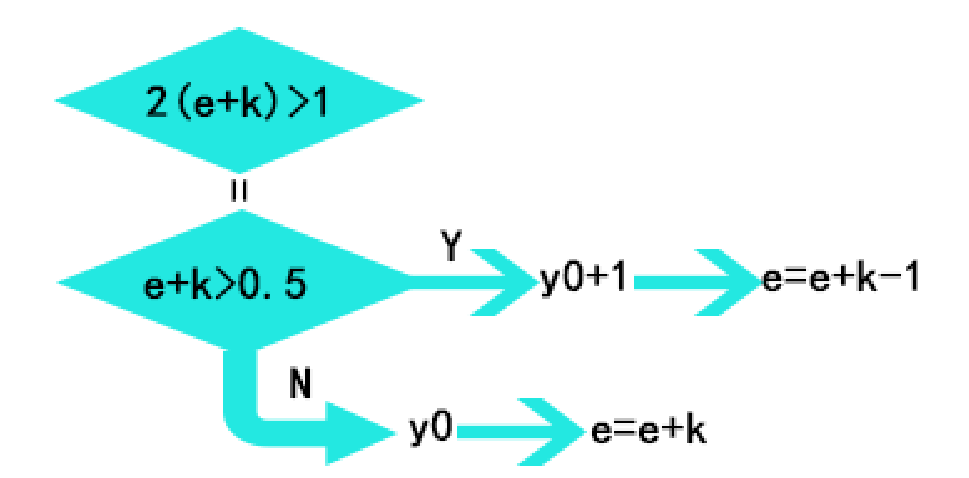
那么程序为:
void LineB2(int x0,int y0,int x1,int y1,int color,CDC *p){ int i,x,y,dx,dy; float k,e; dx=x1-x0; dy=y1-y0; k=(float)dy/dx; e=-0.5;x=x0;y=y0; for(i=0;i<=dx;i++){ p->SetPixel(x,y,color); x=x+1; e=e+k; if(e>=0){ y+=1; e=e-1; } } }
上面的程序中e使用了多次除法运算,算法效率低。
优化
将上面的k使用dy/dx替换,并且同乘dx后,令ξ=dx*e则:
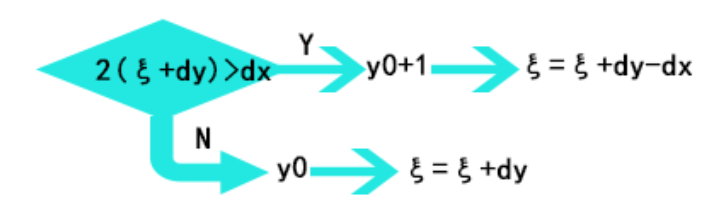
则程序为:
//在程序中e为上面的ξ
void LineB3(int x0,int y0,int x1,int y1,int color,CDC *p){ int i,x,y,dx,dy; float e=0; dx=x1-x0; dy=y1-y0; e=-0.5;x=x0;y=y0; for(i=0;i<=dx;i++){ p->SetPixel(x,y,color); x=x+1; if(2*(e+dy)>=dx){ y+=1; e=e+dy-dx; }else{ e=e+dy; } } }
2、y为阶跃步长(直线光栅化) 适用于k>1的情况
同上可以推出:
可以知道机器在画每一个点的时候都会有误差,则画出的第一个点的坐标(x0,y0)也相当于是(x0+e,y0),那么可以知道下个点的坐标为红色的p(x0+e+1/k,y0+1),但是机器在画p点时,如果p点的横坐标不是整数时,应该进行判断这个点是接近右边(x0+1,y0+1)还是接近蓝左边(x0,y0+1),最后如果接近右边则e累积1、k-1,如果接近左边则e累积1/k
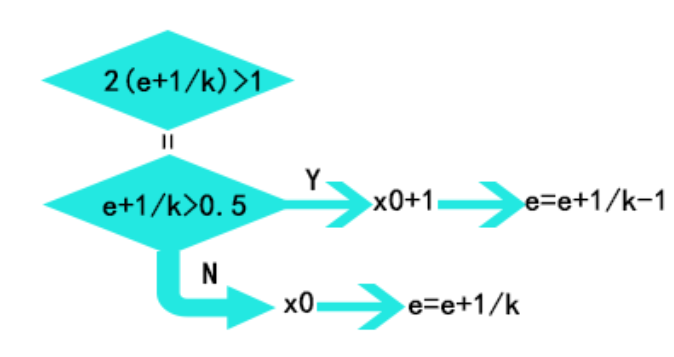
优化得:
将上面的k使用dy/dx替换,并且同乘dy后,令ξ=dy*e则:
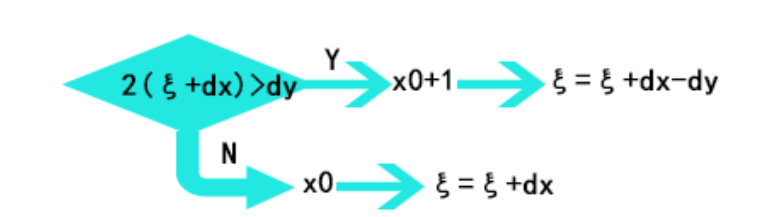
对于k<-1和-1<=k<=0可以通过对x取相反数来实现(与以上两种情况关于y轴对称)