leetcode -- Sqrt(x)

Implement int sqrt(int x).

Compute and return the square root of x.

[解题思路]

使用二分法来求解开方，在一个区间中，每次拿中间数的平方来试验，如果小了，再拿右区间的中间数来试。

比如求解sqrt(16), (0+16) / 2 = 8, 8*8 = 64 > 16, 选择左区间(0+7)/2 = 3, 3*3 = 9 < 16, 继续选择右区间(4 + 7)/2 = 5, 5*5 = 25 > 16

继续选择左区间(4+4)/2 = 4, 4*4=16

这里为了防止x输入过大时，mid*mid会溢出，把mid*mid与x的比较换成mid与x/mid之间的比较

public int sqrt(int x) {
        // Start typing your Java solution below
        // DO NOT write main() function
        int start = 0, end = x;
        while(start <= end){
            int mid = start + (end - start) / 2;
            if(mid == 0){
                if(x == 0){
                    return x;
                } else {
                    start = mid + 1;
                    continue;
                }
            }
            if(mid < x / mid){
                start = mid + 1;
            } else if(mid > x / mid){
                end = mid - 1;
            } else {
                return mid;
            }
        }
        return (start + end) / 2;
    }

2013-10-29 refactor code:

public int sqrt(int x) {
        // IMPORTANT: Please reset any member data you declared, as
        // the same Solution instance will be reused for each test case.
        if(x == 0 || x == 1){
            return x;
        }
        int start = 0, end = x;
        while(start <= end){
            int mid = start + (end - start)/2;
            if(mid == x / mid){
                return mid;
            } else if(mid < x / mid){
                start = mid + 1;
            } else {
                end = mid - 1;
            }
        }
        
        return (start + end) / 2;
    }

2.牛顿迭代法

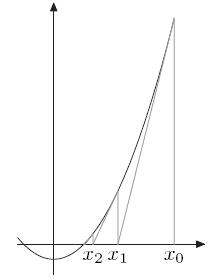
   为了方便理解，就先以本题为例：

   计算x² = n的解，令f(x)=x²-n，相当于求解f(x)=0的解，如左图所示。

   首先取x₀，如果x₀不是解，做一个经过(x₀,f(x₀))这个点的切线，与x轴的交点为x₁。

   同样的道理，如果x₁不是解，做一个经过(x₁,f(x₁))这个点的切线，与x轴的交点为x₂。

   以此类推。

   以这样的方式得到的x_i会无限趋近于f(x)=0的解。

   判断x_i是否是f(x)=0的解有两种方法：

   一是直接计算f(x_i)的值判断是否为0，二是判断前后两个解x_i和x_i-1是否无限接近。

经过(x_i, f(x_i))这个点的切线方程为f(x) = f(x_i) + f’(x_i)(x - x_i)，其中f'(x)为f(x)的导数，本题中为2x。令切线方程等于0，即可求出x_i+1=x_i - f(x_i) / f'(x_i)。

继续化简，x_i+1=x_i - (x_i² - n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (x_i + n/x_i) / 2。

public int sqrt(int x) {
        // Start typing your Java solution below
        // DO NOT write main() function
        
        if(x <= 0){
            return x;
        }
        double last = 0;
        double cur = x;
        while(Math.abs(cur - last) > 0.0001){
            last = cur;
            cur = (cur + x / cur) / 2;
        }
        return (int)cur;
    }