机器学习中的数学知识-线性代数

1、矩阵叉乘（内积）

矩阵的乘法就是矩阵a的第一行乘以矩阵b的第一列，各个元素对应相乘然后求和作为第一元素的值。

矩阵只有当左边矩阵的列数等于右边矩阵的行数时,它们才可以相乘,乘积矩阵的行数等于左边矩阵的行数,乘积矩阵的列数等于右边矩阵的列数 。

2.矩阵点乘（外积）

矩阵点乘是对应位置相乘，表征向量的映射。

向量和矩阵的范数，L1范数和L2范数

范数定义：

两个标量我们可以比较大小，比如1，2，我们知道2比1大。但是现在如果是两个向量(1,2,1) (2,2,0)，我们如何比较大小呢？此时我们把一个向量通过不同的方法，映射到一个标量，从而可以比较大小，这个标量学名就叫做“范数”。

向量范数也可以分为0范数，1范数，2范数，p范数，∞范数等。

L1范数：向量1-范数也就是求X向量各元素之和。

L2范数：向量2-范数又欧几里德范数，也就是求X向量各元素平方和，再开方。

单位矩阵

任何矩阵与单位矩阵相乘都等于本身，用E表示，

逆矩阵定义： 

一个n阶方阵A称为可逆的，或非奇异的，如果存在一个n阶方阵B，使得

则称B是A的一个逆矩阵。A的逆矩阵记作A-1。

逆矩阵性质定理

1. 可逆矩阵一定是方阵。
2. 如果矩阵A是可逆的，其逆矩阵是唯一的。
3. A的逆矩阵的逆矩阵还是A。记作（A-1）-1=A。
4. 可逆矩阵A的转置矩阵AT也可逆，并且（AT）-1=（A-1）T (转置的逆等于逆的转置）
5. 若矩阵A可逆，则矩阵A满足消去律。即AB=O（或BA=O），则B=O，AB=AC（或BA=CA），则B=C。
6. 两个可逆矩阵的乘积依然可逆。
7. 矩阵可逆当且仅当它是满秩矩阵。

行列式的定义与计算方法

矩阵行列式是指矩阵的全部元素构成的行列式，设A=(aij)是数域P上的一个n阶矩阵，则所有A=(aij)中的元素组成的行列式称为矩阵A的行列式，记为|A|或det(A)。

一个n×n矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和，即

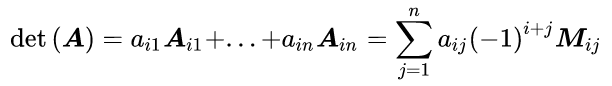
行列式意义：

行列式就是矩阵对应的线性变换对空间的拉伸程度的度量，或者说物体经过变换前后的体积比。

行列式为0的矩阵，不可逆；行列式不为零的矩阵，可逆。

线性变换A的行列式是否为零，就代表了其映射的保真性，也即，能不能把一组线性无关的矢量变换成另一组保持无关性的矢量。

举例说明，我们假设A是一个3维的矩阵。如果映射前，有一组三个线性无关的矢量，我们知道它们张成的体积不是0；经过映射后，他们对应的新矢量也能张成一个平行六面体，那么这个平行六面体的体积就是原体积乘以A的行列式。显然，如果A的行列式是0，那么变换后的新“平行六面体"的体积将不可避免的也是0。根据上文的结论，我们有：变换后的这一组新矢量线性相关。 

         

伴随矩阵

伴随矩阵用处：

A*A=|A|
A的伴随乘以A矩阵等于A的行列式,伴随矩阵因此提出

矩阵的秩：

保证一组更少数目矢量的线性无关性。这个数目往往少于A的维度（或者说，线性空间的维度），这个数目就叫做线性变换A的秩。
二次型的定义

二次型（quadratic form）：n个变量的二次多项式称为二次型，即在一个多项式中，未知数的个数为任意多个，但每一项的次数都为2的多项式。

二次型例子：

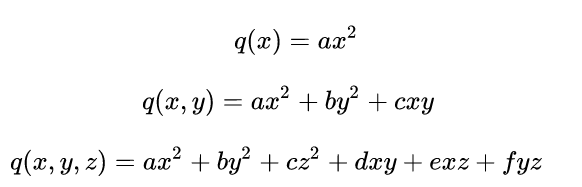
矩阵的正定性
矩阵的特征值与特征向量
矩阵的奇异值分解
线性方程组的数值解法，尤其是共轭梯度法