一、简介
KNN(k-nearst neighbors,KNN)作为机器学习算法中的一种非常基本的算法,也正是因为其原理简单,被广泛应用于电影/音乐推荐等方面,即有些时候我们很难去建立确切的模型来描述几种类别的具体表征特点,就可以利用天然的临近关系来进行分类;
二、原理
KNN算法主要用于分类任务中,用于基于新样本与已有样本的距离来为其赋以所属的类别,即使用一个新样本k个近邻的信息来对该无标记的样本进行分类,k是KNN中最基本的参数,表示任意数目的近邻,在k确定后,KNN算法还依赖于一个带标注的训练集,对没有分类的测试集中的样本进行分类,KNN确定训练集中与该新样本“距离”最近的k个训练集样本,并将新样本类别判定到这k个近邻中占比最大的那个类中,下面是一个广泛传播的KNN示例(图源自网络):

蓝色与红色的样本点即为上述的已标注训练样本集,绿色样本点为待标记的新样本,这时k取值的重要性就体现了出来:
1.当k=3时,在图中实线圈中包含了离新样本最近的3个训练样本点,因为此时红色样本数目为2,蓝色样本数目为1,根据最大占比原则,绿色样本点自然而然的被判定为红色所属类别;
2.当k=5时,在图中虚线圈中包含了离新样本最近的5个训练样本点,因为此时蓝色样本数目为3,红色样本数目为2,根据最大占比原则,绿色样本点被判定为蓝色所属类别;
从上面的例子中可以看出,不同的k值对最终的分类结果的影响非常明显,一般来说,k值满足下列规律:k值越大,算法的泛化能力越强,在训练集上的表现越差;k值越小,算法在训练集上的误差越小,也更有可能导致泛化能力变差;
而在距离的衡量上,一般来说,欧氏距离是最常见的,即:
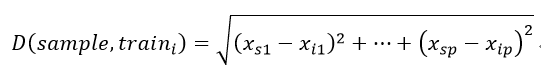
有时也会用到一些特殊的距离,譬如曼哈顿距离(即绝对值距离):
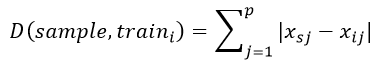
KNN的过程就是找出距离最小的k个训练样本点的过程,而针对数据量大小的不同,有几种不同的算法,下面一一列举:
蛮力法(brute force)
对快速计算最近邻的探索是机器学习中一个活跃的领域,最单纯的近邻搜索方法使用蛮力的方法,也就是直接去运算样本集中每个点与待分类样本间的距离,那么对于含有N个样本维数为D的情况下,蛮力运算的时间复杂度为O[DN2],对于较小的数据集,蛮力运算是比较高效的,但随着N的增长,蛮力运算就变得不太合实际了,想象一下,对于一个千万级别的数据集,使用蛮力运算意味着对每一个待分类的新样本,你都需要进行数千万次的平方和开根号,这实在是一件很愚蠢的事,于是便有了如下几种快速方法;
KD树(KD-tree)
KD树是一种基于模型的算法,它并没有上来就对测试样本分类,而是基于训练集先建立模型,这个模型就称为KD树,通过建立起的模型对测试集进行预测。KD树指的是具有K个特征维度的树,与KNN的参数k不是一个概念,这里我们以大小写来区分;
KD树算法有如下几个步骤:
1.建立KD树
KD树构造树采用的是从样本集中m个样本的n个维度的特征中,分别计算这n个特征各自的方差,用其中方差最大的第k维特征nk来作为根结点,接着针对这个特征,我们选择特征nk的中位数nkm对应的样本点作为划分点,即对所有在nk这个特征上取值小于nkm的样本,将其划入左子树,对于在nk上大于等于nkm的样本,将其划入右子树,接着,对于左子树和右子树,我们采用类似的方法计算方差——挑选最大方差对应的特征——根据该特征的中位数建立左右子树,重复这个过程,以递归的方式生成我们需要的KD树,更严谨的流程图如下:
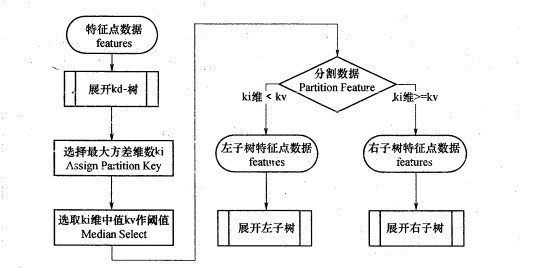
下面以一个非常简单的例子来更形象的展现这个过程:
我们构造数据集{(1,3),(2.5,4),(2,3.4),(4,5),(6.3,4),(7,7)}
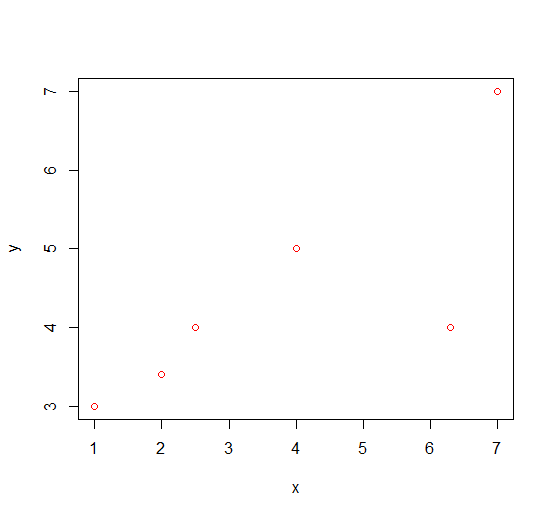
Step1:分别计算x与y的方差,var(x)=5.86,var(y)=2.08,因此我们选择x作为KD树的根结点,此时x的中位数为3.25,构造左子树与右子树,将{(1,3),(2.5,4),(2,3.4)}划入左子树,{(4,5),(6.3,4),(7,7)}划入右子树,此时的划分情况如下图:
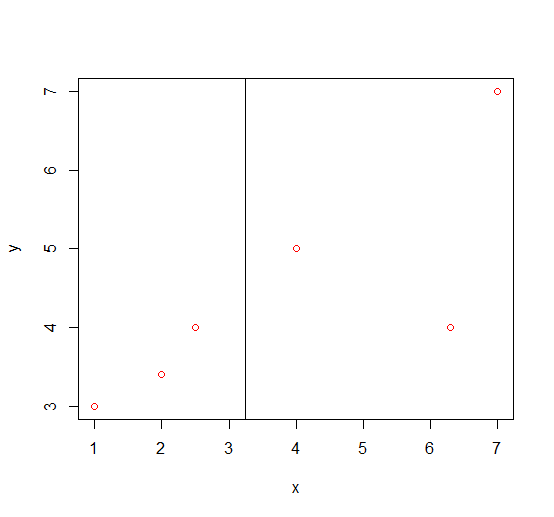
Step2:接着针对左子树中的{(1,3),(2.5,4),(2,3.4)},计算出var(x)=0.5833333,var(y)=0.2533333,因此选择x作为划分特征,此时中位数为2,划分出左-左子树{(1,3)},左-右子树{(2.5,4),(2,3.4)};右子树中的{(4,5),(6.3,4),(7,7)},计算出var(x)=2.463333,var(y)=2.333333,所以选取x作为划分特征,中位数为6.3,划分出右-左子树{(4,5)},右-右子树{(6.3,4),(7,7)},这一轮得到如下划分:

Step3:接下来对样本数未达到1的左-右子树{(2.5,4),(2,3.4)},计算得var(x)=0.125,var(y)=0.18,因此这里选择y进行划分,中位数为3.7,这个路径下所有样本划分完成;对同样样本数未到达1的右-右子树{(6.3,4),(7,7)},var(x)=0.245,var(y)=4.5,选择y进行划分,中位数为5.5,这一轮,也是最终轮得到如下划分:
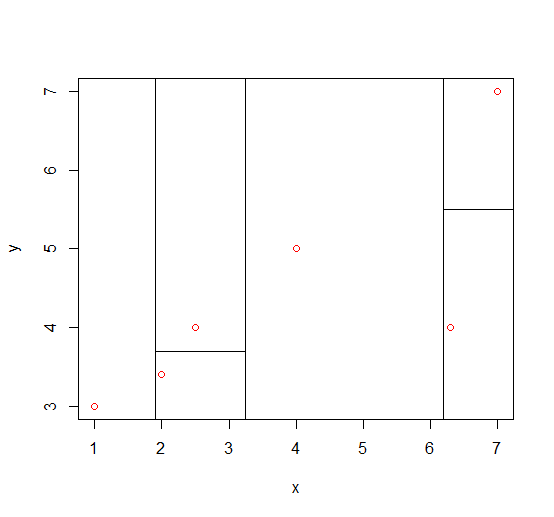
2.KD树搜索最近邻
在KD树建立完成之后,我们可以通过它来为测试集中的样本点进行分类,对于任意一个测试样本点,首先我们在KD树中找到该样本点归入的范围空间,接着以该样本点为圆心,以该样本点与该范围空间中的单个实例点的距离为半径,获得一个超球体,最近邻的点必然属于该超球体,接着沿着KD树向上返回叶子节点的父节点,检查该父节点下另一半子树对应的范围空间是否与前面的超球体相交,如果相交,在该半边子树下寻找是否有更近的最近邻点,若有,更新最近邻点,若无,继续沿着KD树向上到达父节点的父节点的另一半子树,继续搜索有无更近邻,这个过程一直向上回溯到根结点时,算法结束,当前保存的最近邻点即为最终的最近邻。
通过KD树的划分建模,在对新样本进行分类时,可以极大程度减少冗余的最近邻搜索过程,因为很多样本点所在的矩形范围空间与超球体不相交,即不需要计算距离,这大大减少了计算时间,下面还以前面举例中创建的KD树为例,对新样本点(3.4,4.2)进行分类:
Step1:首先我们找到(3.4,4.2)应该归入(4,5)所在的超矩形体内,它与(4,5)的欧氏距离为1,以(3.4,4.2)为圆心,1为半径作圆,得到如下图:
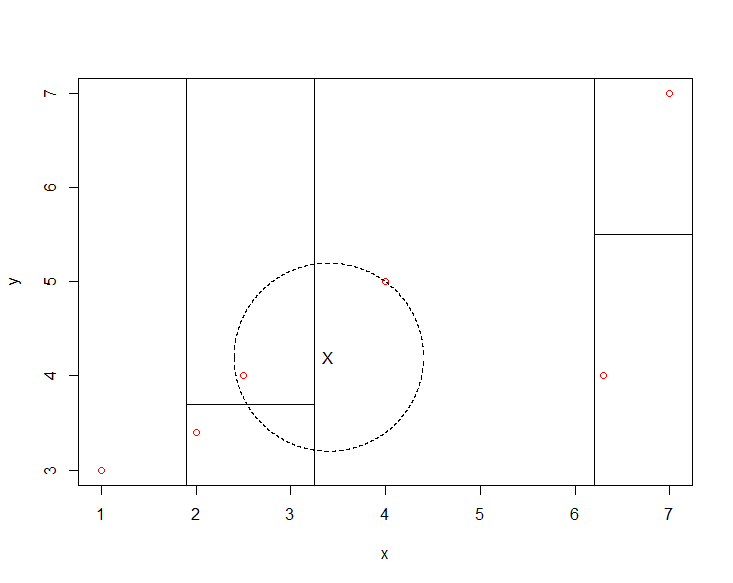
可以看出,该圆与平面x=3.25存在重叠的部分,且在该圆与其他范围空间相交部分存在着距离新样本点更近的实例点(2.5,4),这时将新样本点的最近邻更新为实例点(2.5,4),再作圆,如下图:
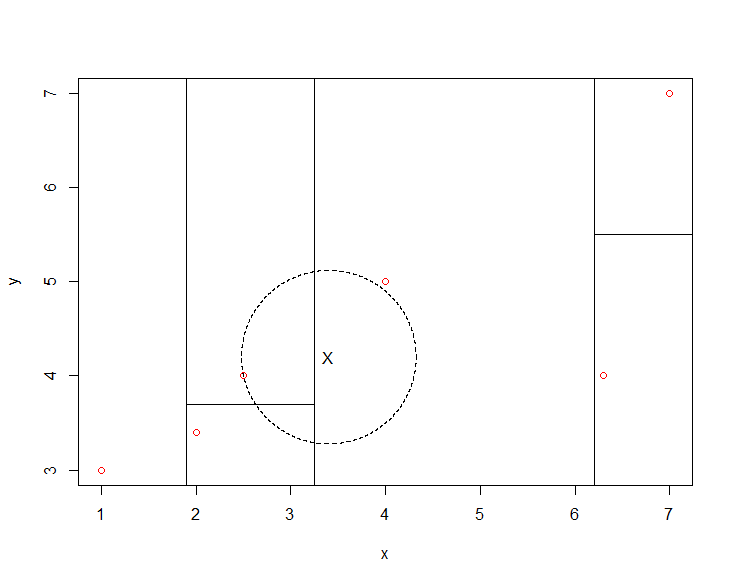
此时该圆虽然与其他矩形范围空间仍然存在着相交部分,但这些部分中已不再存在比实例点(2.5,4)更靠近新样本点的实例点,因此得到最近邻点;
3.基于KD树进行预测
通过上面描述的KD树建模——KD树搜索的过程,我们就可以利用数量合理的训练实例点来训练最佳的KD树,接着对新样本进行预测,在设定的近邻数k下,一,通过KD树完成第一轮的搜索,找到最近的近邻点;二、利用同样的步骤,在将已搜索到的近邻点从KD树中移除的条件下,用递归的方式对余下的k-1个待寻近邻点进行迭代搜索;三,在所需k个最近邻点都寻得的基础上,利用最大占比原则完成类别的预测。
球树法(ball tree)
KD树法虽然快捷高效,但在遇到维度过高的数据或分布不均匀的数据集时效率也不太理想,譬如,以我们上面使用过的例子:

在这一轮中,图中X距离左边上部矩形内的实例点已经非常之近,但因为它也与左边下部矩形空间有些许相交部分,因此仍然需要重复对左边下部区域内的点计算其与样本点的距离,这在维度较高时,就成了灾难,会出现数量非常庞大的冗余的范围空间需要计算,这是由于KD树中以平行于坐标轴的多条线段划分训练集,形成矩形结构导致的,因为他们都有突出去的棱角,容易与圆相交;
为了优化这一情况,球树诞生了,这种结构可以大幅度优化上面所说的问题;
球树的算法有如下几个步骤:
1.建立球树
球树得名于它利用超球体而不是超立方体来分割空间:
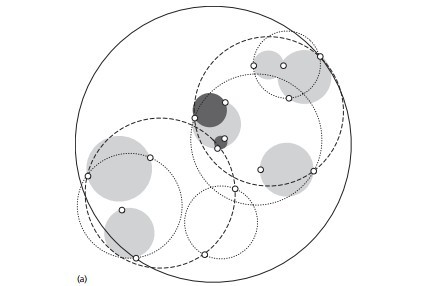
Step1:先构建一个超球体,这个超球体是能够包含所有样本点的最小超球体;
Step2:根据确定的超球体球心,先选择超球体中距离球心最远的那个点,再选择超球体中距离球心次远的那个点,用类似K-means聚类的思想,将剩余的点归类到这两个点中最近的那个点的聚类群中,接着计算这两个聚类群的聚类中心(重心),以及聚类群能够包含所有群内样本点的最小半径,再分别构造两个超球体(类似KD树中的左右子树);
Step3:重复上面的步骤,对子超球体进一步细分,最终得到分割出每一个训练样本的超球体的集合;
KD树和球树思想类似,区别在于球树的划分空间为超球体,KD树得到的是超立方体,因为在半径等于边长的情况下,得到的球体体积必然比立方体体积要小很多,这样在计算高维和巨量数据时就可以避免很多多余的搜索。
2.球树搜索最近邻
因为球树与KD树的划分空间形状特点不同,它会有很多空余出来的空间(譬如一个超球体内部除去其两个子超球体外的其他空间),这使得其无法像KD树那样依据范围空间在一开始就对新样本点进行初始定位(因为新样本点可能会落入最底层超球体之间空余的空间内),因此球树找出给定目标点的最近邻方法是自上而下从根结点出发,向下逐层为新样本点定位,并在最终确定的叶子中找到与其最为接近的点,并确定一个最近邻距离的上限值(类似线性规划中割平面法定上限的过程),接着类似KD树,建立起以新样本点为球心,上限值为半径的超球体,检查该超球体是否与其他球树中的超球体有相交的部分,若有,则计算所有相交超球体内部点与新样本点的距离,若上限值得到更新,则继续这个过程直到上限值不再收敛;否则直接将上限值对应的点标记为这一轮的最近邻点,利用球树预测时也是类似KD树预测的步骤,递归搜索,直到找到所需的k个结点为止;
三、评价
作为一种简单又高效的机器学习算法,其主要优缺点如下:
优点:
1、原理简单
2、训练过程的时间复杂度较低
3、无需对数据分布作出假设,准确度高,且鲁棒性强,对异常值不敏感
4、对分类任务中类与类之间重叠区域较多的情况,KNN较为合适
5、适合各个类训练样本数量较多的情况
缺点:
1、对样本严重不平衡的情况效果较差,即对比例处于劣势的类别预测精度低下
2、KD树、球树的建模过程往往会消耗大量内存,尤其在训练样本集较大时
3、属于lazy learning,导致预测时速度比不上逻辑回归等可用表达式计算的分类器
4、可解释性较差,所以经常用于难以解释内部关系时的分类任务
5、计算量大,容易陷于高维灾难
下面分别在Python和R中实现KNN算法;
四、Python
在Python中,我们使用sklearn.neighbors中的KNeighborsClassifier()来进行常规的KNN分类,其主要参数如下:
n_neighbors:int型,控制近邻数k,默认是5
weights:控制KNN算法中对不同数据分布情况的不同策略,'uniform'代表所有数据都是均匀分布在样本空间中的,这时所有近邻权重相等;'distance'表示近邻的权重与距离成反比,即距离越大权重越小,越近的近邻贡献越大。这个权重被应用于最终的近邻代表投票的过程中,默认是'uniform'
algorithm:字符型,控制KNN具体使用的算法,'ball_tree'代表球树法,'kd_tree'表示KD树法,'brute'表示蛮力运算法,'auto'表示算法自动去决定使用哪一种方法最好
leaf_size:int型,默认为30,控制球树或KD树中叶子中的最小样本个数,越小意味着树的构建越精细,也意味着越费内存
p:int型,默认值为2,这个参数对应Minkowski距离中的不同情况,p取1时为绝对值距离,p取2时为欧氏距离
metric:字符型,控制构造树时距离的类型,默认是Minkowski距离,配合p=2,即为标准的欧氏距离
n_jobs:int型,控制并行运算使用到的CPU核心数,默认是1,即单核,-1时为开启所有核心
下面以我们喜闻乐见的鸢尾花数据为例进行演示:
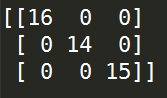
from sklearn.neighbors import KNeighborsClassifier from sklearn import datasets from sklearn.metrics import confusion_matrix from sklearn.model_selection import train_test_split '''加载鸢尾花数据''' X,y = datasets.load_iris(return_X_y=True) '''留出法分割训练集与验证集''' X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3) '''搭建KNN分类器''' clf = KNeighborsClassifier(algorithm='brute', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=1, n_neighbors=5, p=2, weights='uniform') '''利用训练数据对KNN进行训练''' clf = clf.fit(X_train,y_train) '''利用训练完成的KNN分类器对验证集上的样本进行分类''' pre = clf.predict(X_test) '''打印混淆矩阵''' print(confusion_matrix(y_test,pre))
运行结果:

我们将近邻权重参数weights调为'distance':
'''搭建KNN分类器''' clf = KNeighborsClassifier(algorithm='brute', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=1, n_neighbors=5, p=2, weights='distance') '''利用训练数据对KNN进行训练''' clf = clf.fit(X_train,y_train) '''利用训练完成的KNN分类器对验证集上的样本进行分类''' pre = clf.predict(X_test) '''打印混淆矩阵''' print(confusion_matrix(y_test,pre))
运行结果:
五、R
在R中有多个包可以实现KNN算法,我们这里简单介绍class包中的knn(),其主要参数如下:
train:训练集的自变量部分,数据框或矩阵形式
test:待预测的新样本,数据框或矩阵形式
cl:训练集的特征对应的真实类别
k:整数型,控制KNN的近邻数
prob:逻辑型参数,默认为F,设置为T时,输出的结果里还会包含每个样本点被归类的概率大小
下面依然以鸢尾花数据进行演示:
> library(class) > > #载入鸢尾花数据 > data(iris) > > #留出法分割训练集与验证集 > sam <- sample(1:dim(iris)[1],dim(iris)[1]*0.7) > train <- iris[sam,] > test <- iris[-sam,] > > #训练KNN分类器并输出test的预测结果 > Kclf <- knn(train=train[,-5],test=test[,-5],cl=train[,5],k=5,prob=T) > > #打印混淆矩阵 > table(test[,5],Kclf) Kclf setosa versicolor virginica setosa 18 0 0 versicolor 0 11 3 virginica 0 0 13 > > #打印正确率 > sum(diag(prop.table(table(test[,5],Kclf)))) [1] 0.9333333
以上就是关于KNN算法的基本内容,如有笔误,望指出。