（数据科学学习手札11）K-means聚类法的原理简介&Python与R实现

kmeans法（K均值法）是麦奎因提出的，这种算法的基本思想是将每一个样本分配给最靠近中心（均值）的类中，具体的算法至少包括以下三个步骤：

　　1.将所有的样品分成k个初始类；

　　2.通过欧氏距离将某个样品划入离中心最近的类中，并对获得样品与失去样品的类重新计算中心坐标；

　　3.重复步骤2，直到所有的样品都不能在分类为止

kmeans法与系统聚类法一样，都是以距离的远近亲疏为标准进行聚类的。但是两者的不同之处也很明显：系统聚类对不同的类数产生一系列的聚类结果，而K均值法只能产生指定类数的聚类结果。具体类数的确定，离不开实践经验的积累。有时也可借助系统聚类法，以一部分样本（简单随机抽样）为对象进行聚类，其结果作为K均值法确定类数的参考。

kmeans算法以k为参数，把n个对象分为k个聚类，以使聚类内具有较高的相似度，而聚类间的相似度较低。相似度的计算是根据一个聚类中对象的均值来进行的。kmeans算法的处理流程如下：随机地选择k个对象，每个对象初始地代表了一个簇的平均值或中心；对剩余的每个对象，根据其与各个聚类中心的距离将其赋给最近的簇；重新计算每个簇的平均值作为聚类中心进行聚类。这个过程不断重复，直到准则函数收敛，得到最终需要的k个类，算法结束；准则函数通常采用最小平方误差准则：

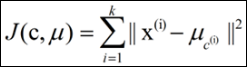
关于k具体数值的选择，在实际工作大多数是根据需求来主观定（如衣服应该设计几种尺码），在这方面能够较直观的求出最优k的方法是肘部法则，它是绘制出不同k值下聚类结果的代价函数，选择最大拐点作为最优k值。

而在Python与R中都各自有实现K-means聚类的方法，下面一一介绍：

Python

Python的第三方包中可以用来做Kmeans聚类的包有很多，本文主要介绍Scipy和sklearn中各自集成的方法；

1.利用Scipy.cluster中的K-means聚类方法

scipy.cluster.vq中的kmeans方法为kmeans2(data,n),data为输入的样本数据矩阵，样本x变量的形式；n为设定的聚类数。

这里我们分别生成5个100x10的高维正态分布随机数，标准差均为0.8，均值分别为1,2,3,4,5，并将其拼接为500x10的矩阵，并按行打乱顺序进行聚类，鉴于维度为10大于2，为了在二维平面上进行可视化，我们使用sklearn包中的降维方法TSNE来对样本数据进行10维至2维的降维以可视化，具体代码如下：

import numpy as np
from scipy.cluster.vq import *
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

'''生成示例数据'''
set1 = np.random.normal(1,0.8,(100,10))
set2 = np.random.normal(2,0.8,(100,10))
set3 = np.random.normal(3,0.8,(100,10))
set4 = np.random.normal(4,0.8,(100,10))
set5 = np.random.normal(5,0.8,(100,10))

'''将两个列数相同的矩阵上下拼接，类似R中的rbind()'''
data = np.concatenate((set1,set2,set3,set4,set5))

'''按行将所有样本打乱顺序'''
np.random.shuffle(data)

'''进行kmeans聚类'''
res, idx = kmeans2(data,5)

'''为不同类的样本点分配不同的颜色'''
colors = ([([0.4,1,0.4],[1,0.4,0.4],[0.4,0.4,0.4],[0.4,0.4,1.0],[1.0,1.0,1.0])[i] for i in idx])

'''对样本数据进行降维以进行可视化'''
data_TSNE = TSNE(learning_rate=100).fit_transform(data)

'''绘制所有样本点（已通过聚类结果修改对应颜色）'''
plt.scatter(data_TSNE[:,0],data_TSNE[:,1],c=colors,s=12)
plt.title('K-means Cluster')

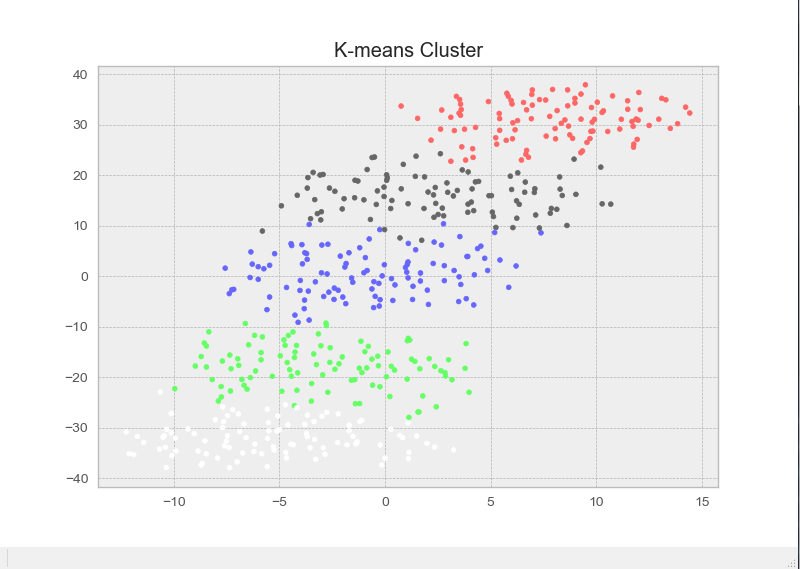
可以看出，我们通过kmeans顺利的将这些数据分到五个类中（有一类颜色为白色），足以见得kmeans在对常规数据的聚合上效果较好，下面我们假装事先不知道样本数据准确的分类数目，利用肘部法则来选取最优k值：

import numpy as np
from scipy.cluster.vq import *
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from scipy.spatial.distance import cdist
from matplotlib.ticker import MultipleLocator

xmajorLocator   = MultipleLocator(1)
'''生成示例数据'''
set1 = np.random.normal(1,0.5,(100,10))
set2 = np.random.normal(8,0.5,(100,10))


'''将两个列数相同的矩阵上下拼接，类似R中的rbind()'''
data = np.concatenate((set1,set2))

'''按行将所有样本打乱顺序'''
np.random.shuffle(data)

K = range(1,5)
cost = []
'''记录代价变化情况'''
for k in K:
    res, idx = kmeans2(data, k)
    cost.append(sum(np.min(cdist(data,res,'euclidean'),axis=1))/data.shape[0])

'''绘制代价变化图'''
ax = plt.subplot(111)
plt.plot(K,cost)
ax.xaxis.set_major_locator(xmajorLocator)
plt.title('cost change')

可以看出，在k=2的时候，我们找到了对应的‘肘部’，这与真实的类数相同，下面我们进行真实类数较多时的k值选择：

import numpy as np
from scipy.cluster.vq import *
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from scipy.spatial.distance import cdist
from matplotlib.ticker import MultipleLocator
from matplotlib import style

xmajorLocator   = MultipleLocator(1)
'''生成示例数据'''
set1 = np.random.normal(1,1,(100,10))
set3 = np.random.normal(2,1,(100,10))
set4 = np.random.normal(3,1,(100,10))
set6 = np.random.normal(4,1,(100,10))


'''将两个列数相同的矩阵上下拼接，类似R中的rbind()'''
data = np.concatenate((set1,set3,set4,set6))

'''按行将所有样本打乱顺序'''
np.random.shuffle(data)

K = range(2,6)
cost = []
'''记录代价变化情况'''
plt.figure(figsize=(12,8))
for k in K:
    res, idx = kmeans2(data, k)
    '''为不同类的样本点分配不同的颜色'''
    colors = ([['red','blue','black','yellow','green'][i] for i in idx])

    '''对样本数据进行降维以进行可视化'''
    data_TSNE = TSNE(learning_rate=100).fit_transform(data)

    '''绘制所有样本点（已通过聚类结果修改对应颜色）'''
    plt.subplot(219+k)
    style.use('bmh')
    plt.scatter(data_TSNE[:, 0], data_TSNE[:, 1], c=colors, s=12)
    plt.title('K-means Cluster of {}'.format(str(k)))
    cost.append(sum(np.min(cdist(data,res,'euclidean'),axis=1))/data.shape[0])

'''绘制代价变化图'''
ax = plt.subplot(111)
plt.plot(K,cost)
ax.xaxis.set_major_locator(xmajorLocator)
plt.title('cost change')

以下是不同类数时的聚类图以及代价函数变化图：

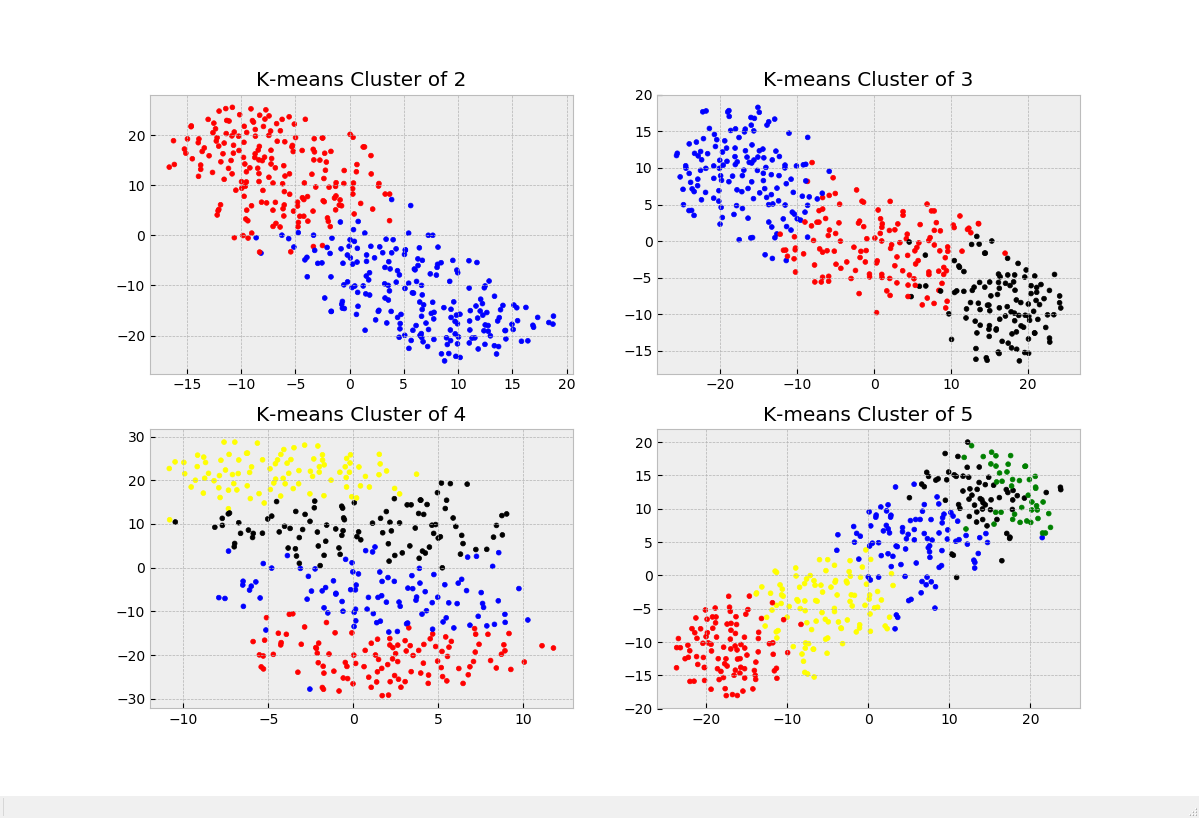
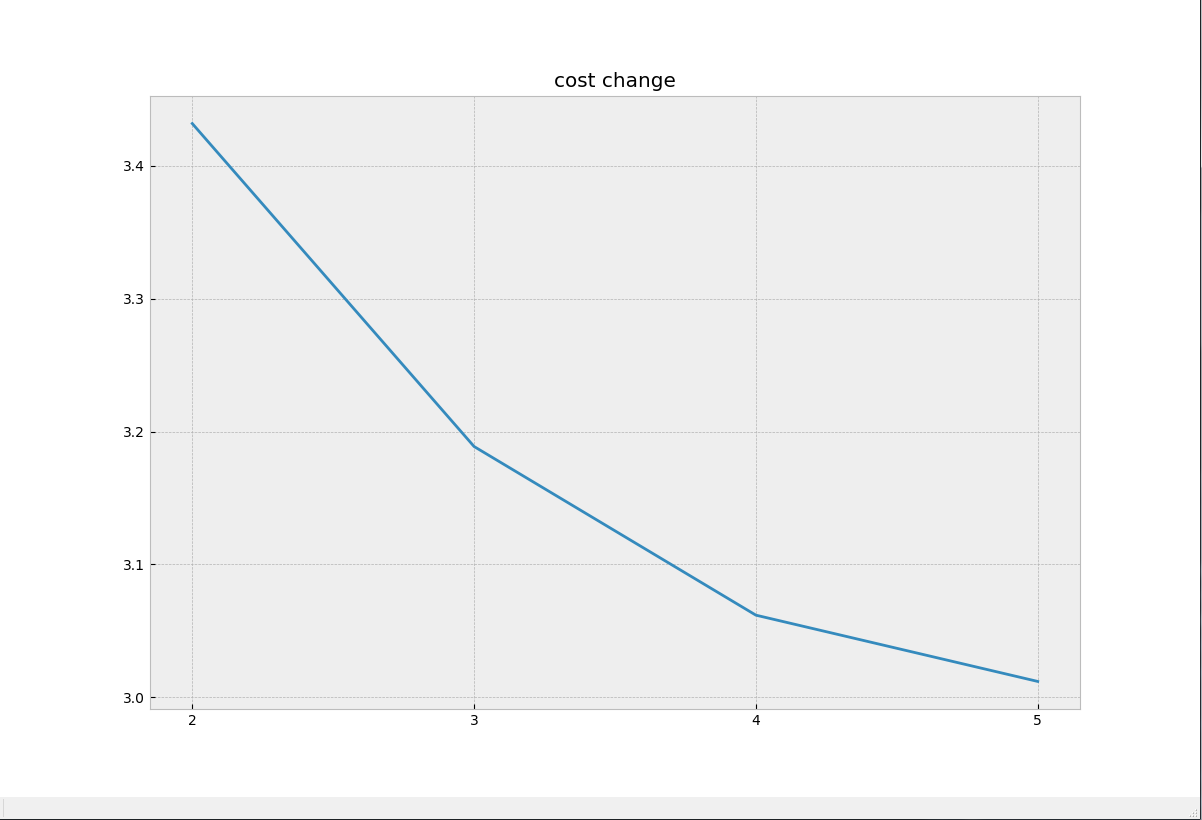
可以看出，在各个类的真实分类较为均匀的时候，肘部法则就失去了意义，因为这时我们无法分辨代价函数的减小是得益于k选的好还是k值的增大。

2.利用sklearn中的方法进行K-means聚类

 作为Python中赫赫大名的机器学习包，sklearn中封装的kmeans算法也非常成熟稳定，sklearn.cluster中的KMeans(n_clusters=n,init,n_jobs).fit(data)：n_clusters表示设定的聚类个数k，默认为8；init表示初始选择簇中心的方法，有‘kmeans++’与‘random’；n_jobs用来控制线程，-1为CPU全开

from sklearn.manifold import TSNE
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt

'''生成聚类样本数据'''
set1 = np.random.normal(1,0.7,(100,10))
set2 = np.random.normal(2,0.7,(100,10))
set3 = np.random.normal(3,0.7,(100,10))

data = np.concatenate((set1,set2,set3))
np.random.shuffle(data)

'''生成可视化需要的2维降维数据'''
data_tsne = TSNE(learning_rate=100).fit_transform(data)
colors = ['b', 'g', 'r', 'y', 'k', 'c', 'm', 'chartreuse']
plt.figure(figsize=(12,8))

'''对不同的k值设定进行聚类并绘图'''
for i in range(2,8):
    kmeans_model = KMeans(n_clusters=i,init='random',n_jobs=-1).fit(data)#sklearn中的kmeans方法
    color = [colors[k] for k in kmeans_model.labels_]
    plt.subplot(229+i)
    plt.scatter(data_tsne[:,0],data_tsne[:,1],color=color)
    plt.title('{} clusters'.format(str(i)))

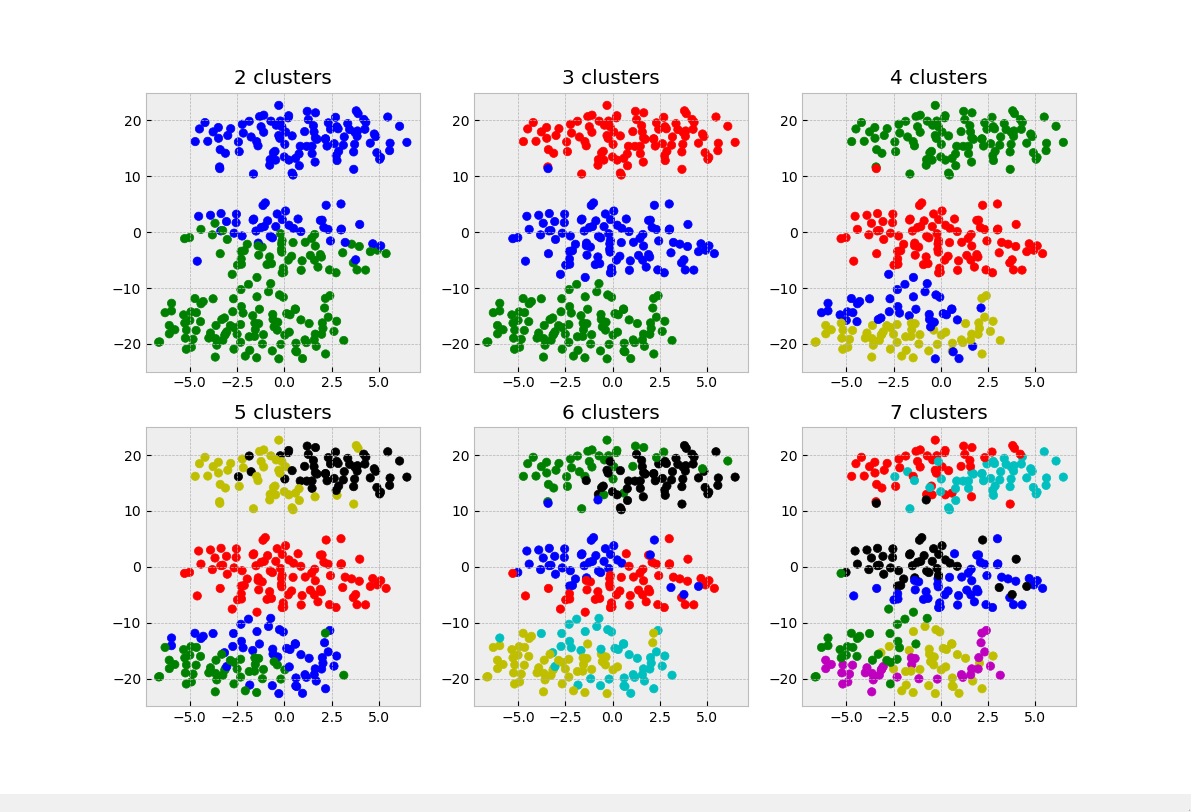
从主观上看，k=3时效果最好，这也与真实样本的分布类数一致。

R

在R中做K-means聚类就非常轻松了，至少不像Python那样需要安装第三方包，在R中自带的kmeans(data,centers,iter.max)可以直接用来做K-means聚类，其中data代表输入的待聚类样本，形式为样本x变量，centers代表设定的聚类簇数量，iter.max代表算法进行迭代的最大次数，一般比较正常的数据集不会消耗太多次迭代；下面针对低维样本与高维样本分别进行K-means聚类：

一、低维

这里我们生成两类正态分布随机数据，分别是0均值0.7标准差，和3均值0.7标准差，将其拼接在一起，共10000x2的矩阵作为输入变量，设置k分别等于2,3,4,5来看看聚类结果的不同：

#kmeans聚类法
library(RColorBrewer)

data1 <- matrix(rnorm(10000,mean=0,sd=0.7),ncol=2)
data2 <- matrix(rnorm(10000,mean=5,sd=0.7),ncol=2)
data <- rbind(data1,data2)

pch1 <- rep('1',5000)
pch2 <- rep('2',5000)
#设置颜色
cols<-brewer.pal(n=5,name="Set1")
par(mfrow=c(2,2))
for(i in 2:5){
  cl <- kmeans(data,centers = i,iter.max = 10)
  plot(data,col=cols[cl$cluster],pch=c(pch1,pch2),cex=0.9)
  title('K-means Result')
  points(cl$centers,col='yellow',pch='x',cex=1.5)
}

聚类结果可视化如下：

二、高维

当样本数据的维度远远大于3时，就需要对其进行降维至2维以进行可视化，和前面所说的TSNE类似，R中也有同样功能的降维包Rtsne，下面我们就对一个维度较高的（10维）的样本数据集进行聚类及降维可视化：

#kmeans聚类法
library(Rtsne)
library(RColorBrewer)

data1 <- matrix(rnorm(10000,mean=0,sd=0.7),ncol=10)
data2 <- matrix(rnorm(10000,mean=5,sd=0.7),ncol=10)
data3 <- matrix(rnorm(10000,mean=10,sd=0.7),ncol=10)
data <- rbind(data1,data2,data3)

#设置对应样本的点型
pch1 <- rep('1',length(data[,1])*0.5)
pch2 <- rep('2',length(data[,1])*0.5)
pch3 <- rep('3',length(data[,1])*0.5)
#设置颜色
cols<-brewer.pal(n=5,name="Set1")
#数据的降维（降至2维）
tsne <- Rtsne(data)
#自定义代价函数计算函数
Mycost <- function(data,centers_){
  l <- length(data[,1])
  d <- matrix(0,nrow=l,ncol=length(centers_[,1]))
  for(i in 1:l){
    for(j in 1:length(centers_[,1])){
      dd <- 0
      for(k in 1:length(data[1,])){
        dd <- dd + (data[i,k]-centers_[j,k])^2
      }
      d[i,j] <- sqrt(dd)
    }
  }
  mindist <- apply(d,1,min)
  return(sum(mindist))
}
opar <- par(no.readonly = TRUE)
#初始化代价函数记录向量
zb <- c()
par(mfrow=c(2,2))
#分别根据不同的k进行聚类并可视化
for(i in 2:5){
  cl <- kmeans(data,centers = i,iter.max = 10)
  plot(tsne$Y,col=cols[cl$cluster],pch=c(pch1,pch2,pch3),cex=0.9)
  title(paste(as.character(i),'Clusters'))
  zb[i-1] <- Mycost(data,cl$centers)
}
par(opar)

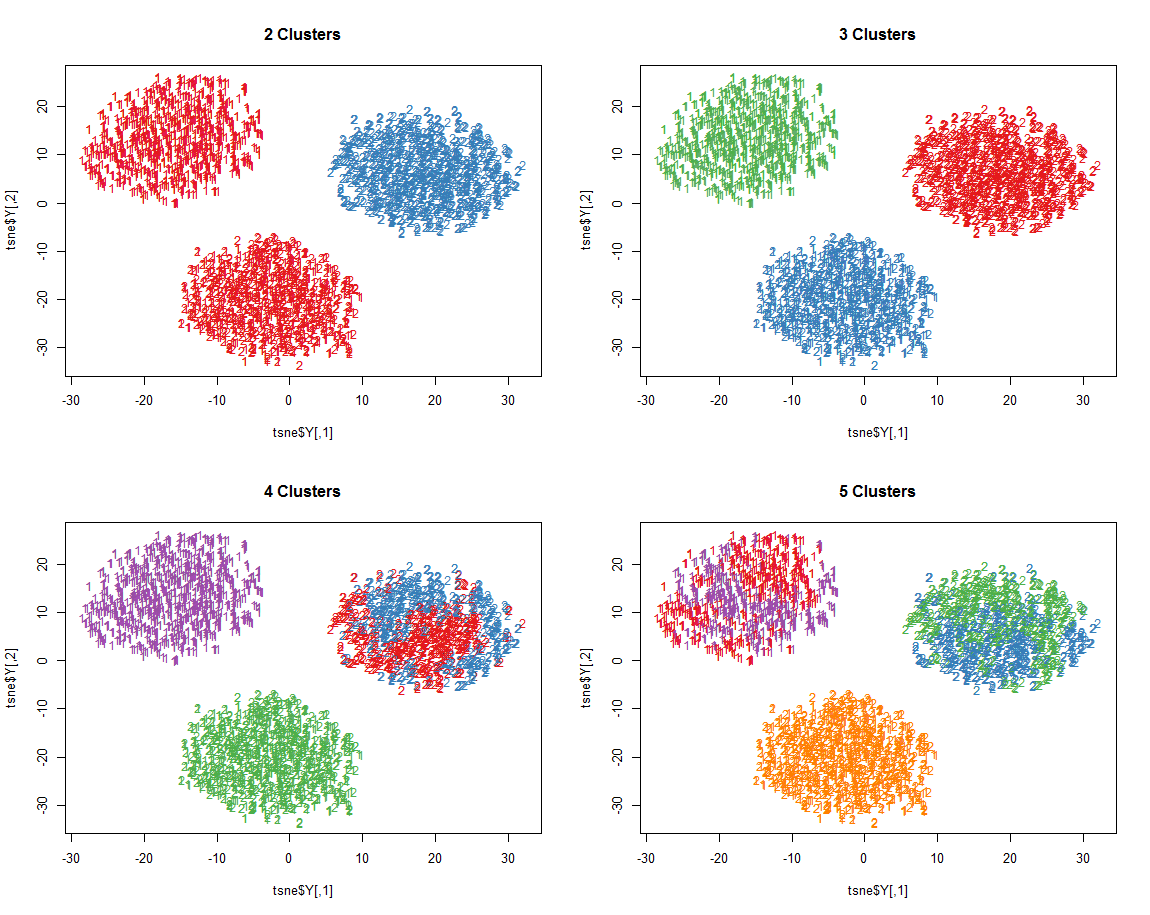
绘制代价函数变化图：

#绘制代价函数随k的增加变化情况
plot(2:5,zb,type='o',xaxt='n',xlab='K值',ylab='Cost')
axis(1,at=seq(2,5,1))
title('Cost Change')

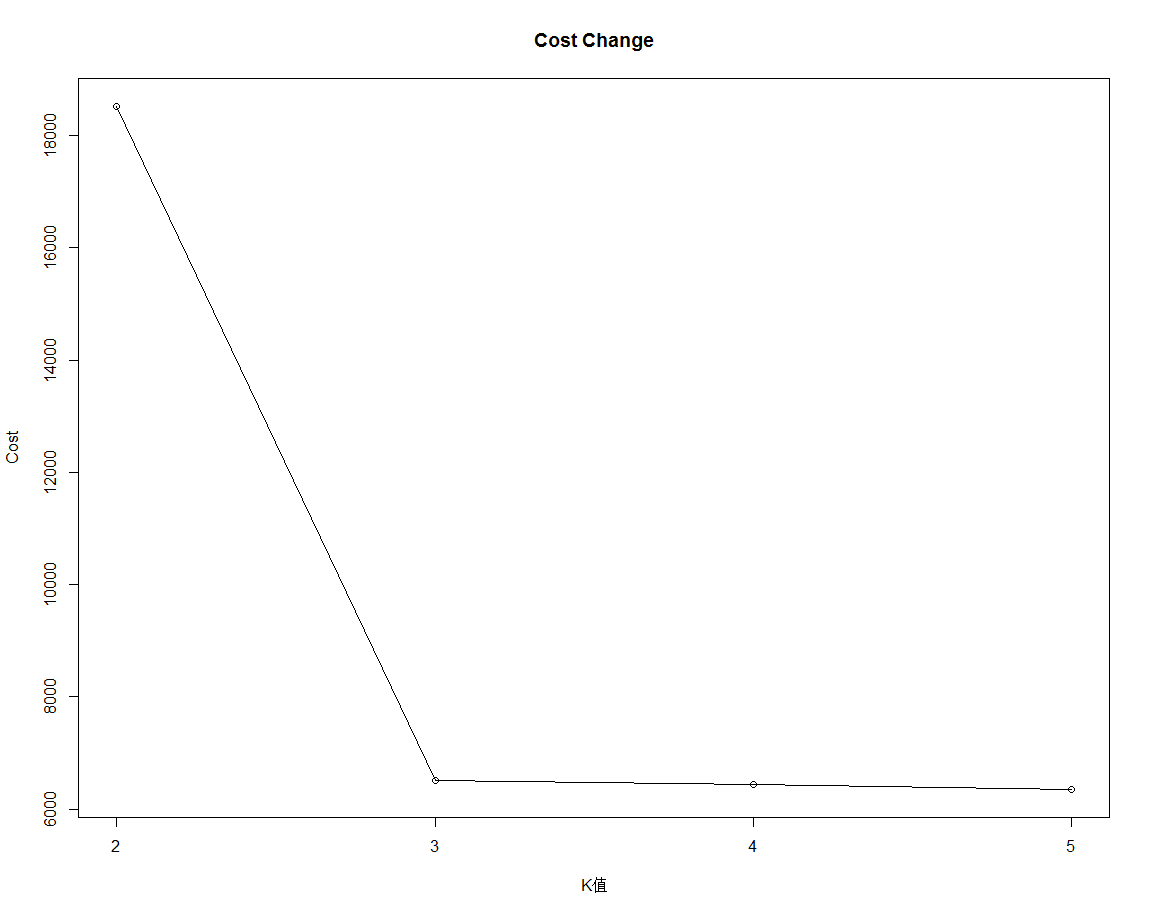
总结：Python与R在K-means上各有各的有点，Python方法众多，运算速度快，只是一些细节不够到位；R非常专业，过程也很简洁，只是在运算速度上稍逊一筹，如果让笔者以后实际工作选择的话，我还是更倾向于R，因为其kmeans函数非常“听话”，严格按照设置的类去分，虽然有时会出现一些不合理的地方；Python则没那么“听话”，有些时候，如果被它的算法内部判定为不可再分，则它会在设定的K值下产生一些任性的空类。

如有发现笔者写错的地方，望多多指出。