
算法背景
KMP算法是由Knuth-Morris-Pratt 算法(简称 KMP),这个算法是由高德纳(Donald Ervin Knuth)和沃恩 · 普拉特在 1974 年构思,同年詹姆斯 ·H· 莫里斯也独立地设计出该算法,最终由三人于 1977 年联合发表。
算法要解决的问题
给定一个字符串S和一个模式串P,要求找出P在S中首次出现的位置,及串的匹配问题。
暴力查找算法
当初次遇到这个问题的时候,肯定脑海中想到的第一反应就是暴力查找匹配,即遍历 S 的每个字符,以该字符为始与 P 比较,全部匹配就输出;否则直到 S 结束。代码如下:
var strStr = function(haystack, needle) {
if (haystack === needle) return 0;
var i = 0;
var j = 0;
while (i < haystack.length && j < needle.length) {
if (haystack.charAt(i) === needle.charAt(j)) {
j++;
} else {
i = i - j;
j = 0;
}
i++;
}
return j === needle.length ? i - j : -1;
};
上述算法的时间复杂度为 O( nm) ,其中 n 为 S 的长度,m 为 P 的长度。这种时间复杂度很难满足我们的需求,接下来进入正题:时间复杂度为 Θ (n+m ) 的 KMP 算法。
KMP算法
理解前缀和后缀的概念


由上图所得, "前缀" 指除了最后一个字符以外,一个字符串的全部头部组合;"后缀" 指除了第一个字符以外,一个字符串的全部尾部组合。
算法流程
1)

首先,主串 "BBC ABCDAB ABCDABCDABDE" 的第一个字符与模式串 "ABCDABD" 的第一个字符,进行比较。因为 B 与 A 不匹配,所以模式串后移一位。
2)

因为 B 与 A 又不匹配,模式串再往后移。
3)

就这样,直到主串有一个字符,与模式串的第一个字符相同为止。
4)

接着比较主串和模式串的下一个字符,还是相同。
5)

直到主串有一个字符,与模式串对应的字符不相同为止。
6)

这时,最自然的反应是,将模式串整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把 "搜索位置" 移到已经比较过的位置,重比一遍。
7)

一个基本事实是,当空格与 D 不匹配时,你其实知道前面六个字符是 "ABCDAB"。KMP 算法的想法是,设法利用这个已知信息,不要把 "搜索位置" 移回已经比较过的位置,而是继续把它向后移,这样就提高了效率。
8)
j 0 1 2 3 4 5 6 7
模式串 A B C D A B D '�'
next[j] -1 0 0 0 0 1 2 0
怎么做到这一点呢?可以针对模式串,设置一个跳转数组int next[ ],这个数组是怎么计算出来的,后面再介绍,这里只要会用就可以了。
9)

已知空格与 D 不匹配时,前面六个字符 "ABCDAB" 是匹配的。根据跳转数组可知,不匹配处 D 的 next 值为 2,因此接下来从模式串下标为 2 的位置开始匹配。
10)

因为空格与C不匹配,C 处的 next 值为 0,因此接下来模式串从下标为 0 处开始匹配。
11)

因为空格与 A 不匹配,此处 next 值为 - 1,表示模式串的第一个字符就不匹配,那么直接往后移一位
12)

逐位比较,直到发现 C 与 D 不匹配。于是,下一步从下标为 2 的地方开始匹配。
13)

逐位比较,直到模式串的最后一位,发现完全匹配,于是搜索完成。
next 数组是如何求出的TOC
next 数组的求解基于 “前缀” 和“后缀”,即next[j]等于P[0]...P[j-1]最长的相同前后缀的长度(请暂时忽视 j 等于 0 时的情况,下面会有解释)。我们依旧以上述的表格为例,为了方便阅读,我复制在下方了。
j 0 1 2 3 4 5 6 7
模式串 A B C D A B D '�'
next[j] -1 0 0 0 0 1 2 0
1)j=0,对于模式串的首字符,我们统一为next[0]=-1;
(2)j=1,前面的字符串为A,其最长相同前后缀长度为 0,即next[1]=0;
(3)j=2,前面的字符串为AB,其最长相同前后缀长度为 0,即next[2]=0;
(4)j=3,前面的字符串为ABC,其最长相同前后缀长度为 0,即next[3]=0;
(5)j=4,前面的字符串为ABCD,其最长相同前后缀长度为 0,即next[4]=0;
(6)j=5,前面的字符串为ABCDA,其最长相同前后缀为A,即next[5]=1;
(7)j=6,前面的字符串为ABCDAB,其最长相同前后缀为AB,即next[6]=2;
(8)j=7,前面的字符串为ABCDABD,其最长相同前后缀长度为 0,即next[7]=0。
那么,为什么根据最长相同前后缀的长度就可以实现在不匹配情况下的跳转呢?举个代表性的例子:假如j=6时不匹配,此时我们是知道其位置前的字符串为ABCDAB,仔细观察这个字符串,首尾都有一个AB,既然在j=6处的 D 不匹配,我们为何不直接把j=2处的 C 拿过来继续比较呢,因为都有一个AB啊,而这个AB就是ABCDAB的最长相同前后缀,其长度 2 正好是跳转的下标位置。
有的读者可能存在疑问,若在j=5时匹配失败,按照我讲解的思路,此时应该把j=1处的字符拿过来继续比较,但是这两个位置的字符是一样的啊,都是B,既然一样,拿过来比较不就是无用功了么?其实不是我讲解的有问题,也不是这个算法有问题,而是这个算法还未优化,关于这个问题在下面会详细说明,不过建议读者不要这里纠结,跳过这个,下面你自然会恍然大悟。
思路如此简单,接下来的问题就是代码实现了,如下:
const getNext = (str, next) => {
var i = 0,
j = -1,
len = str.length;
next[0] = j;
while (i < len) {
if (j === -1 || str.charAt(i) === str.charAt(j)) {
i++;
j++;
next[i] = j;
} else {
j = next[j];
}
}
}
一脸懵逼,是不是。。。
上述代码是求解每个位置的 next 值,即求解每个位置前面字符串的最长相同前后缀的长度。下面具体分析,我把代码分为 3 部分来讲:
(1)i 的作用是什么?
i 为模式串 P 的下标,从 0 开始,程序中我们依次求出next[i]的值,这很简单。
(2)j 的作用是什么?
从next[i]=j;可以很容易推断出,j 代表前后缀最长共有元素的长度。
(3)if...else... 语句里做了什么?
首先我们必须要明确一个事实:若此时i=3,那我们接下来要求解的便是P[0]...p[3]的最长相同前后缀的长度,也就是next[4],而非next[3],这从下面的代码就可以得到证明:
i++;
j++;
next[i] = j;
有了这个事实,下面具体分析:
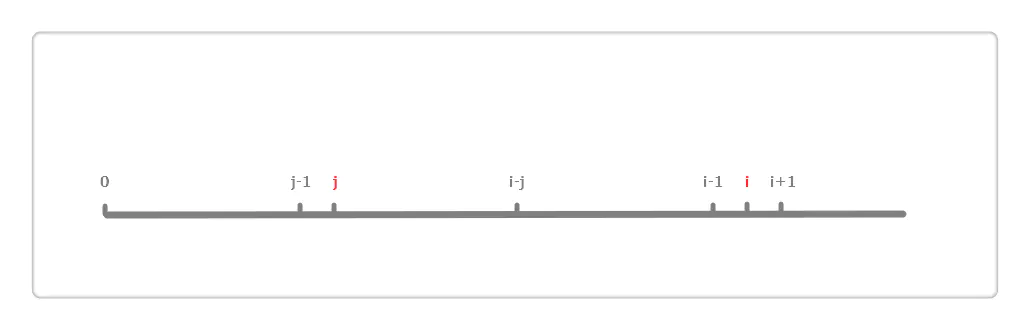
假设 i 和 j 的位置如上图,由next[i]=j得,也就是对于位置 i 来说,区段 0 到 i-1 的最长相同前后缀分别是 0 到 j-1 和 i-j 到 i-1,即这两区段内容相同。
按照算法流程,if(P[i]P[j]),则i++;j++;next[i]=j;;若不等,则j=next[j],见下图:
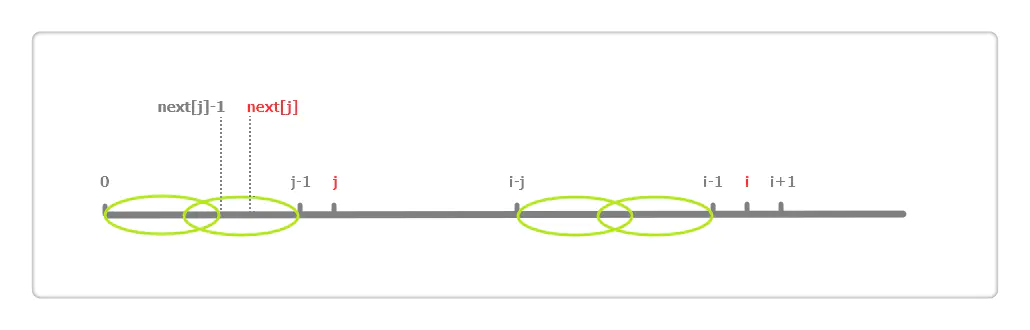
next[j]的含义是 0 到 j-1 区段中最长相同前后缀的长度,如图,用左侧两个椭圆来表示最长相同前后缀,即这两个椭圆代表的区段内容相同;同理,右侧也有相同的两个椭圆。所以 else 语句就是利用第一个椭圆和第四个椭圆内容相同来加快得到 0 到 i-1 区段的相同前后缀的长度。
细心的朋友会问 if 语句中j-1存在的意义是何?第一,程序刚运行时,j 是被初始为 - 1,直接进行P[i]P[j]判断无疑会报错;第二,else 语句中j=next[j],j 是不断后退的,若 j 在后退中被赋值为 - 1(也就是 j=next[0]),在P[i]P[j]判断也会报错。综上两点,其意义就是为了特殊边界判断。
KMP完整代码
const strStr = function (haystack, needle) {
var next = [];
getNext(needle, next);
var i = 0, j = 0;
while (i < haystack.length && j < needle.length) {
if (j === -1 || haystack.charAt(i) === needle.charAt(j)) {
i++;
j++;
} else {
j = next[j];
}
}
return j === needle.length ? i - j : -1;
}
const getNext = (str, next) => {
var i = 0,
j = -1,
len = str.length;
next[0] = j;
while (i < len) {
if (j === -1 || str.charAt(i) === str.charAt(j)) {
i++;
j++;
next[i] = j;
} else {
j = next[j];
}
}
}