Haar分类器使用AdaBoost算法，但是把它组织为筛选式的级联分类器，每个节点是多个树构成的分类器，且每个节点的正确识别率很高。在任一级计算中，一旦获得“不在类别中”的结论，则计算终止。只有通过分类器中所有级别，才会认为物体被检测到。这样的优点是当目标出现频率较低的时候（即人脸在图像中所占比例小时），筛选式的级联分类器可以显著地降低计算量，因为大部分被检测的区域可以很早被筛选掉，迅速判断该区域没有要求被检测的物体。
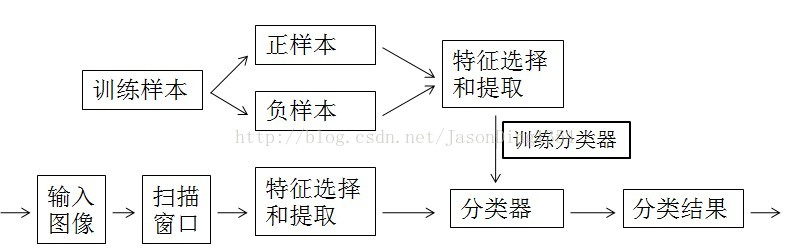
AdaBoost算法就是建立多个弱分类器，给每个弱分类器一个权重，将弱分类器组合在一起，形成一个强分类器。
弱学习（弱分类器）和强学习（强分类器。），所谓的弱学习，就是指一个学习算法对一组概念的识别率只比随机识别好一点，所谓强学习，就是指一个学习算法对一组概率的识别率很高。Kearns和Valiant提出了弱学习和强学习等价的问题 ，并证明了只要有足够的数据，弱学习算法就能通过集成的方式生成任意高精度的强学习方法。
AdaBoost算法的弱分类器不是并行的，是一个弱分类器完成了，下一个才进行，在每个弱分类器进行当中，我们关注的是上一个弱分类器分类错误的数据样本，也就是说用当前分类器来弥补上一个弱分类器分类错误的数据样本；
总的来时，就是后一个弥补前一个分类器的不足。
若第t步样本分类错误，则在第t+1步应该关注上一个分类错误的样本。
α是第t个分类器的权重，Z要让第t+1步权重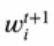
之和为1。
yi是实际值，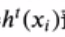
是预测值，当实际值和预测值相等时（预测正确），及下一级这个数据权重会变小，否则下一级这个数据权重增加。
下图 人脸检测的AdaBoost算法流程图
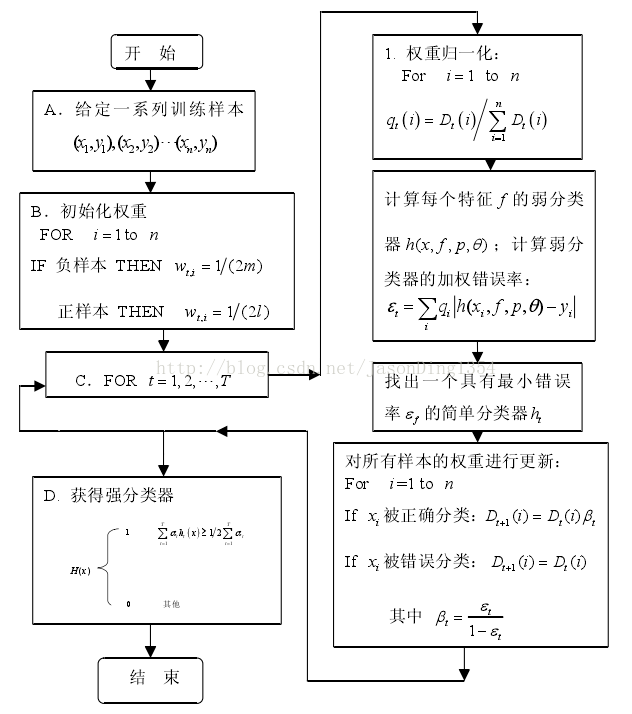
下面讲一讲结构：
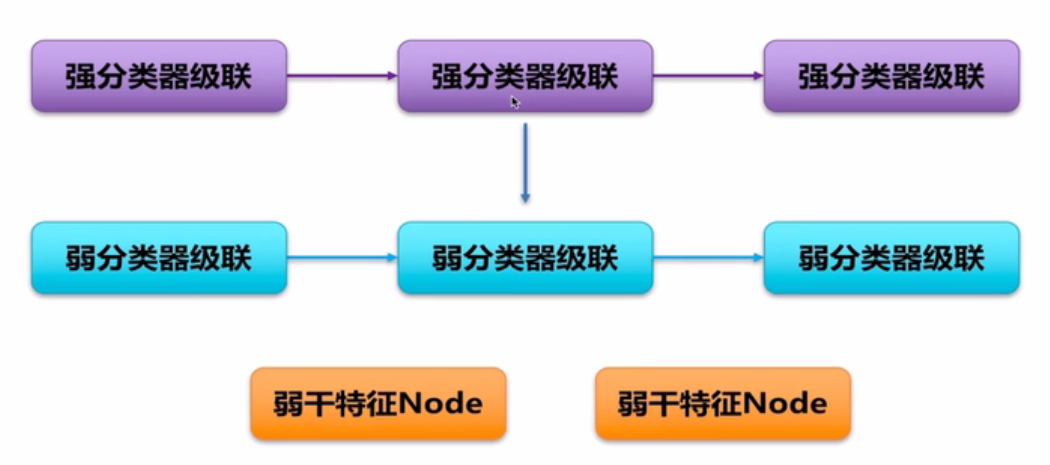
一个AdaBoost级联分类器由若干个强分类器实现，一个强分类器由若干个弱分类器实现，弱分类器又由若干特征构成。
若一个AdaBoost级联分类器由3个强分类器构成，及X1,X2,X3时强分类器的特征，t1,t2,t3及各个强分类器的阈值，
只有X1,X2,X3都大于对应的阈值，才能输出对应的结果；
弱分类器是用来计算强分类器的特征，由上图中x2可得三个弱分类器的特征y1,y2,y3求和得到；
对应的。，弱分类器的特征是由对应的特征节点求出。
一个node节点的harr特征与对应node节点（nodeT1）的阈值判决，z1输出对应的值；
最后求和得到Z，并与弱分类器的判决门限T对比，y1输出对应的值；
总结：
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_moons, make_circles
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import f1_score
import plotly.graph_objs as go
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
class Adaboost_Demonstration:
def __init__(self, X, y, learning_rate=1.):
"""
输入的X为N*2矩阵, y为一维向量, y的值只能取1或-1
:param X: 数据点
:param y: 数据点标记
"""
self.X = X
self.y = y
# 给每个弱分类器一个衰减, 避免过拟合
self.learning_rate = learning_rate
# 样本的个数
self.num_samples = len(self.X)
# 初始化数据样本的权重
self.sample_weight = np.full(self.num_samples, 1 / self.num_samples)
# python list用来存储所有的弱分类器对象
self.classifiers = []
# 储存在每一步的错误率
self.errors_list = []
# 定义弱分类器, 这里我们直接调用sklearn的决策树, max_depth=1代表着这是一个一层决策树, 也就是决策树桩
self.alphas = []
def predict(self, data=None, labels=None, reduction="sign"):
"""
预测数据点的分类
:param reduction: "sign"对弱分类的线性加权组合取符号, "mean"取平均
"""
if data is None:
data = self.X
labels = self.y
# 计算弱分类器线性加权组合的结果
predictions = np.zeros([len(data)]).astype("float")
for classifier, alpha in zip(self.classifiers, self.alphas):
predictions += alpha * classifier.predict(data)
# 对结果取符号
if reduction == "sign":
predictions = np.sign(predictions)
# 对结果求均值
elif reduction == "mean":
predictions /= len(self.classifiers)
# 如果可以的话获取f1 score
if labels is not None and reduction == "sign":
f1 = f1_score(predictions, labels)
return predictions, f1
else:
return predictions
def contour_plot(self, data=None, labels=None, interval=0.2, title="adaboost",
mode="3d"):
"""
等高线图可视化
:param interval: 等高线图网格的间隔
:param title: 等高线图的标题
:param mode: 可选3D或2D可视化
"""
if data is None:
data = self.X
labels = self.y
if labels is None:
labels = np.ones([len(data)])
# 获取网格
x_min, x_max = data[:, 0].min() - .5, data[:, 0].max() + .5
y_min, y_max = data[:, 1].min() - .5, data[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, interval), np.arange(y_min, y_max, interval))
# 将网格的X, Y轴拼接用来进行等高线的计算
X_grid = np.concatenate([np.expand_dims(np.ravel(xx), axis=-1),
np.expand_dims(np.ravel(yy), axis=-1)], axis=-1)
# X_grid的形状[batch(数据点数量), 2]
# 计算分类边界(等高线)
Z_grid = self.predict(data=X_grid, reduction="mean")
Z_grid = Z_grid.reshape(xx.shape)
# 可视化
if mode == "3d":
# 数据点画散点图
scatter = go.Scatter3d(x=data[:, 0], y=data[:, 1], z=self.predict(data=data, reduction="mean"),
mode='markers',
marker=dict(color=labels, size=5, symbol='circle',
line=dict(color='rgb(204, 204, 204)', width=1),
opacity=0.9))
# 等高线3D轮廓图
surface = go.Surface(x=xx, y=yy, z=Z_grid, opacity=0.9)
plot_data = [scatter, surface]
layout = go.Layout(title=title)
# 设置视角
camera = dict(up=dict(x=0, y=0, z=1),
center=dict(x=0, y=0, z=0),
eye=dict(x=1, y=1, z=0.8))
fig = go.Figure(data=plot_data, layout=layout)
fig['layout'].update(scene=dict(camera=camera))
iplot(fig, image="png", filename=title)
if mode == "2d":
# 等高线
plt.contourf(xx, yy, Z_grid, cmap=plt.cm.RdBu, alpha=.8)
# 散点
plt.scatter(data[:, 0], data[:, 1], c=labels,
cmap=ListedColormap(['#FF0000', '#0000FF']), edgecolors='k')
plt.title(title)
plt.show()
def __next__(self, reduction="mean", plot=True, plot_mode="2d"):
# 定义弱分类器(决策树桩)
# classifier = DecisionTreeClassifier(
# max_depth=2,min_samples_split=20,
# min_samples_leaf=5)
classifier = DecisionTreeClassifier(max_depth=1)
# 用弱分类器拟合数据
classifier.fit(self.X, self.y, sample_weight=self.sample_weight)
# 得到弱分类器对数据的推断, 也就是h(x)
predictions = classifier.predict(self.X)
# 计算错误率
error_rate = np.mean(np.average((predictions != self.y), weights=self.sample_weight))
# 计算alpha
alpha = self.learning_rate * (np.log((1 - error_rate) / error_rate)) / 2
# 计算t+1的权重
self.sample_weight *= np.exp(-alpha * self.y * predictions)
# 归一化, 归一化因子为Z: sum(self.sample_weight)
self.sample_weight /= np.sum(self.sample_weight)
# 记录当前弱分类器对象
self.classifiers.append(classifier)
# 记录当前弱分类器权重
self.alphas.append(alpha)
# 计算f1 score
_, f1 = self.predict()
# 画图
if plot:
return self.contour_plot(
title="adaboost step " + str(len(self.classifiers)) + " f1 score: {:.2f}".format(f1), mode=plot_mode)
else:
return f1
if __name__ == '__main__':
# 测试
X, y = make_moons(n_samples=300, noise=0.2, random_state=3)
y[np.where(y == 0)] = -1
model = Adaboost_Demonstration(X, y)
for i in range(100):
model.__next__(plot=False)
model.contour_plot(mode="2d")
参考：https://blog.csdn.net/jasonding1354/article/details/37558287
机器学习之数学之旅-从零推导adaboost与3D可视化-特征选择-集体智能-集成学习-boosting
代码：https://github.com/aespresso/a_journey_into_math_of_ml