前言
掌握好数据结构是我们学习算法的基础。例如基本的数组、链表、二叉树、堆、栈到复杂的图等等。今天我们就来分析一下红黑树是一种怎么样的结构。
基本概念
红黑树是一种自平衡二叉查找树。这里涉及到了几个概念:平衡、二叉、查找。
二叉树:由不同的节点组成,每一个节点有左子节点和右子节点,一个节点最多两个子节点,这种就叫二叉树。
例如: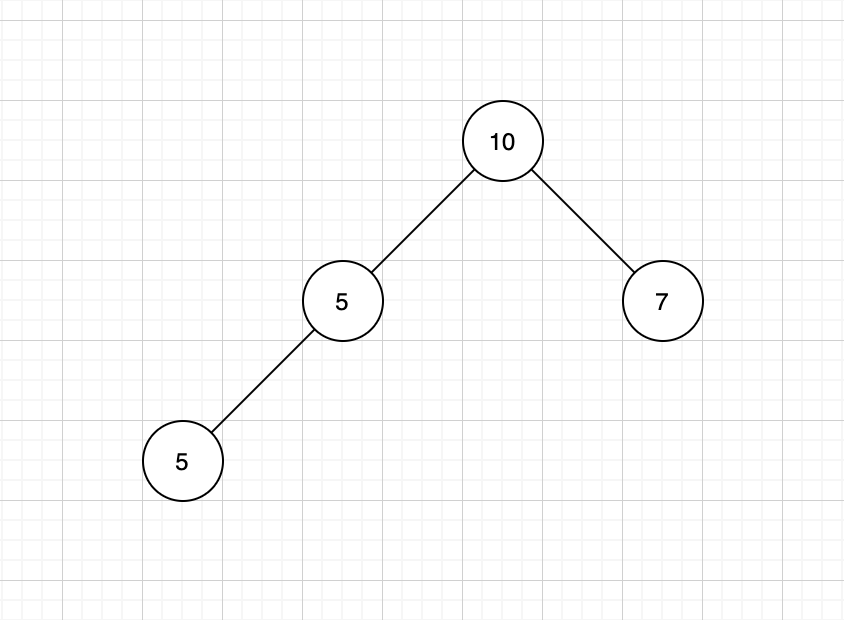
二叉查找树:上图的二叉树是普通的二叉树,有时候我们希望二叉树能具有一些功能便于我们查询节点,这时候就有了二叉查找树,也叫二叉搜索树。二叉查找树的原理是左子节点(包括其子节点)的值小于(可能等于,看使用需求)当前节点,右子节点(包括其子节点)大于当前节点。而且这个原理对每个子节点都适用。这样我们查询的速度就从O(n)变成了O(logn)。
例如: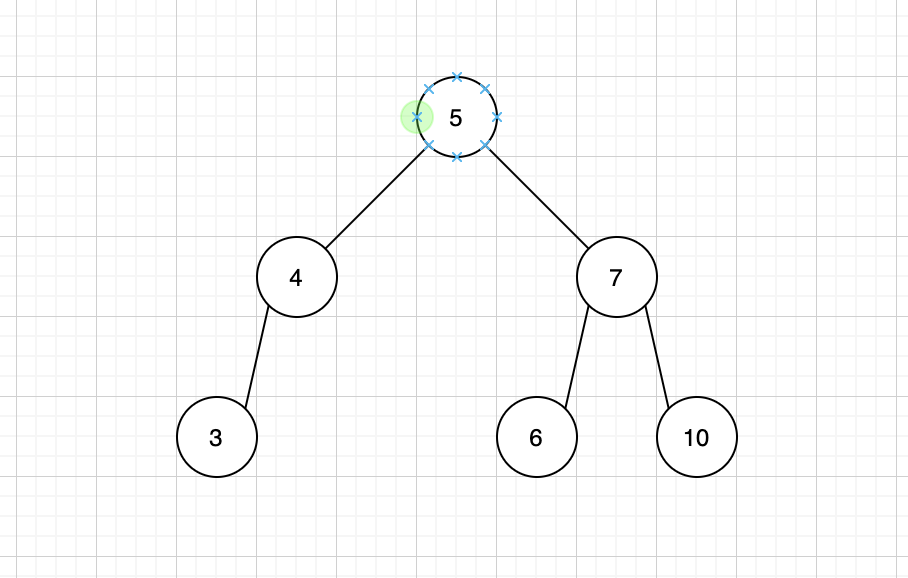
这样看起来挺美好,但是考虑极端情况呢?例如:
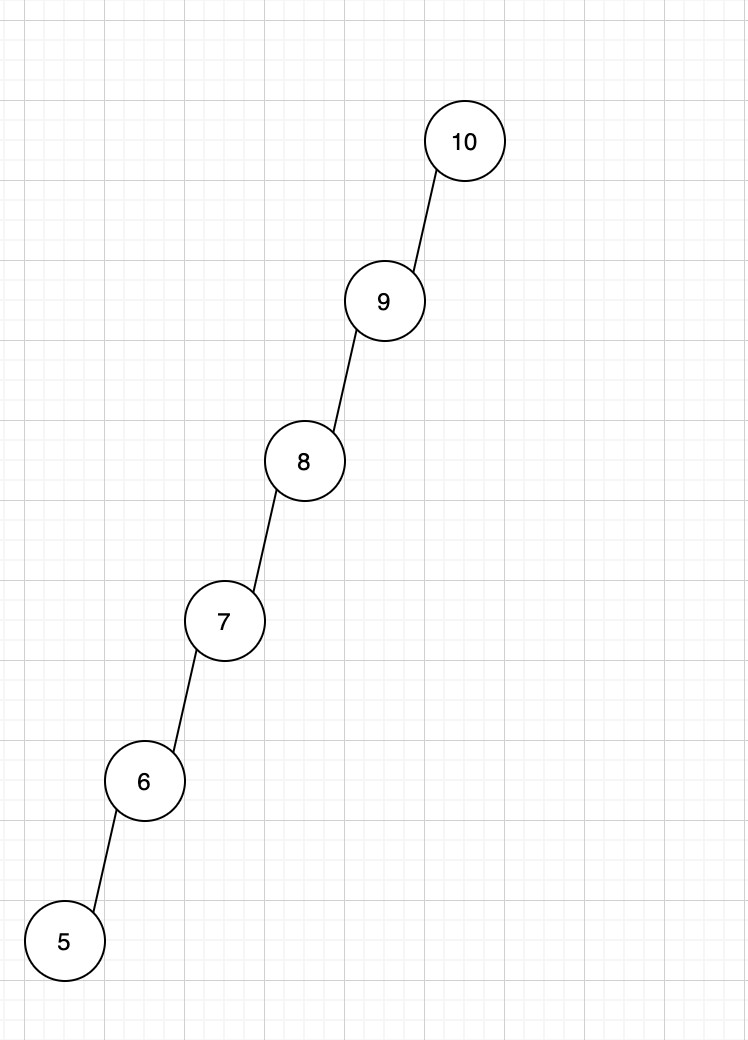
这个样子的树是二叉搜索树吗?是,但是看起来特别不平衡,数据全部堆积在左边,而且最重要的是,这样会导致查询速度从O(logn)退化成了O(n)。
因此,后面又发明了自平衡二叉查找树,有好几种,AVL、红黑树等,其中性能比较好的就是红黑树。Java中的TreeMap结构就使用了这个数据结构,不仅如此,在JDK1.8中HashMap单数组上链表长度超过8便会变成红黑树,来节省map在哈希冲突严重时的查询时间。由此可见红黑树的重要性。
红黑树的定义
- 每个节点要么是红色,要么是黑色
- 根节点是黑色
- 每个叶子节点都是黑色的空节点(null节点)
- 每个红色节点的两个子节点是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
如图: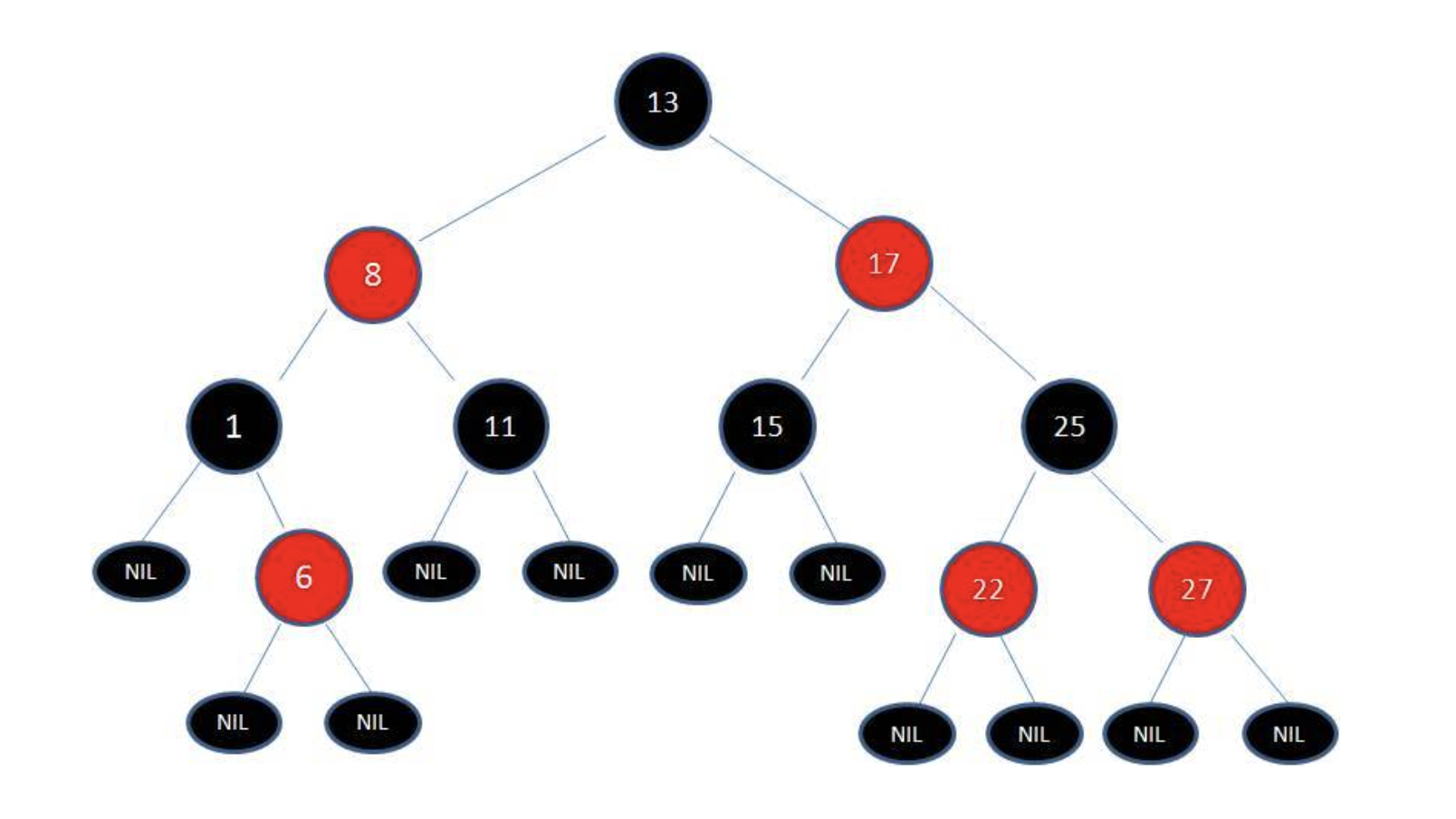
(图转自程序员小灰 https://zhuanlan.zhihu.com/p/31805309)