Given a binary tree, each node has value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.
For all leaves in the tree, consider the numbers represented by the path from the root to that leaf.
Return the sum of these numbers.
Example 1:
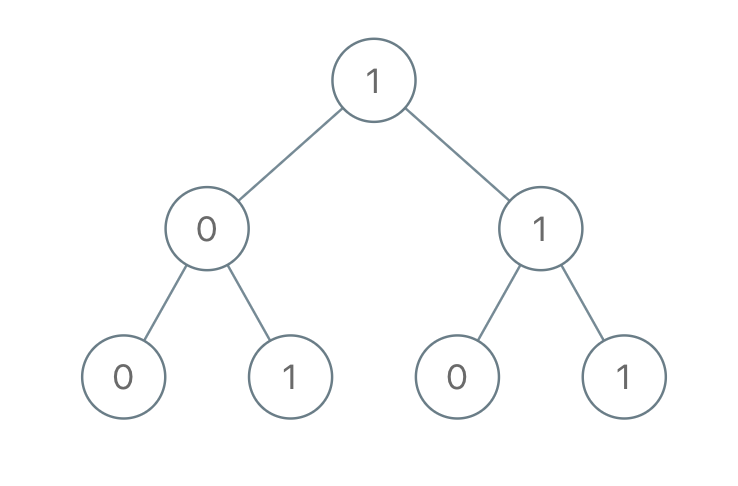
Input: [1,0,1,0,1,0,1]
Output: 22
Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
Note:
- The number of nodes in the tree is between
1and1000. - node.val is
0or1. - The answer will not exceed
2^31 - 1.
M1: optimized, time = O(n), space = O(h)
class Solution { public int sumRootToLeaf(TreeNode root) { return dfs(root, 0); } public int dfs(TreeNode root, int sum) { if(root == null) { return 0; } sum = sum * 2 + root.val; if(root.left == null && root.right == null) { return sum; } return dfs(root.left, sum) + dfs(root.right, sum); } }
M2: naive, find all paths then convert binary to decimal and sum up
time = O(n + k*h) visit all nodes + parse k strings (avg len = h), space = O(h) call stack + O(k) store k paths
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public int sumRootToLeaf(TreeNode root) { List<String> paths = new ArrayList<>(); findPath(root, new StringBuilder(), paths); System.out.println(paths); int sum = 0; for(String path : paths) { sum += Integer.parseInt(path, 2); } return sum; } public void findPath(TreeNode root, StringBuilder sb, List<String> paths) { if(root == null) { return; } sb.append(root.val); if(root.left == null && root.right == null) { paths.add(sb.toString()); sb.deleteCharAt(sb.length() - 1); return; } findPath(root.left, sb, paths); findPath(root.right, sb, paths); sb.deleteCharAt(sb.length() - 1); } }