Given a linked list, determine if it has a cycle in it.
To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.
Example 1:
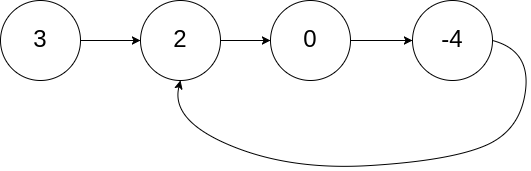
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
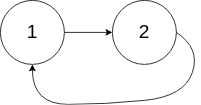
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:
Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Follow up:
Can you solve it using O(1) (i.e. constant) memory?
双指针,如果快慢指针相遇说明有环,如果快指针走到头(null)说明无环
use two pointers, fast and slow, both starting at head, slow moves one step at a time while fast moves two steps at a time. If there is no cycle in the list, the fast pointer will eventually reach the end. keep moving two pointers until fast is pointing to null, if fast equals to slow, it means there's a cycle, return true. otherwise, return false.
time = O(n), space = O(1)
/** * Definition for singly-linked list. * class ListNode { * int val; * ListNode next; * ListNode(int x) { * val = x; * next = null; * } * } */ public class Solution { public boolean hasCycle(ListNode head) { if(head == null || head.next == null) { return false; } ListNode slow = head, fast = head; while(fast != null && fast.next != null) { slow = slow.next; fast = fast.next.next; if(slow == fast) { return true; } } return false; } }