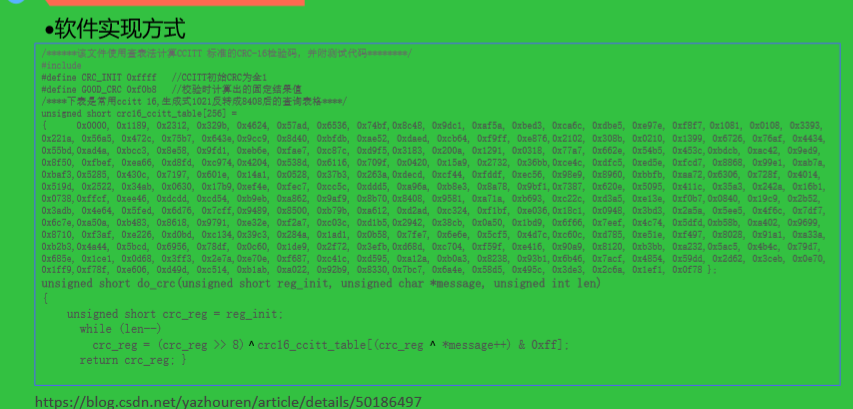
1、CRC校验的基本原理
*增加冗余码(校验位)

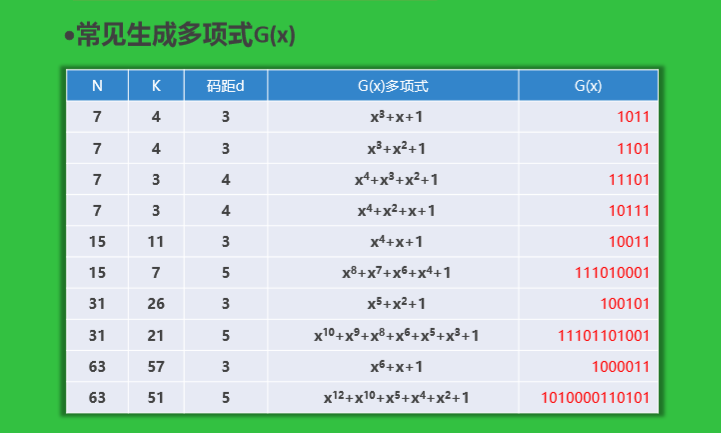
*生成多项式G(x)
收发双方约定的一个(r+1)位二进制数,发送方利用G(x)对信息多项式做模2除运算,生成校验码。接收方利用G(x)对收到的编码多项式做模2除运算检测差错及错误定位。
*G(x)应满足的条件
A、最高位和最低为必须为1
B、当被传送信息(CRC码)任何一位发生错误时,被生成多项式做除后应该使余数不为0;
C、不同位发生错误时,模2除运算后余数不同
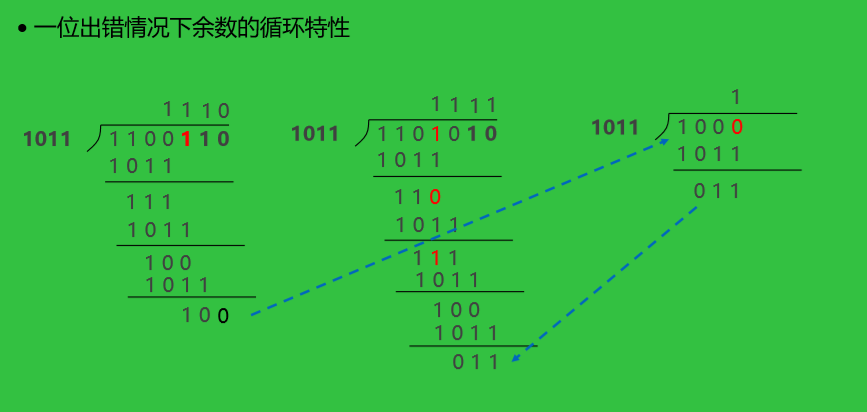
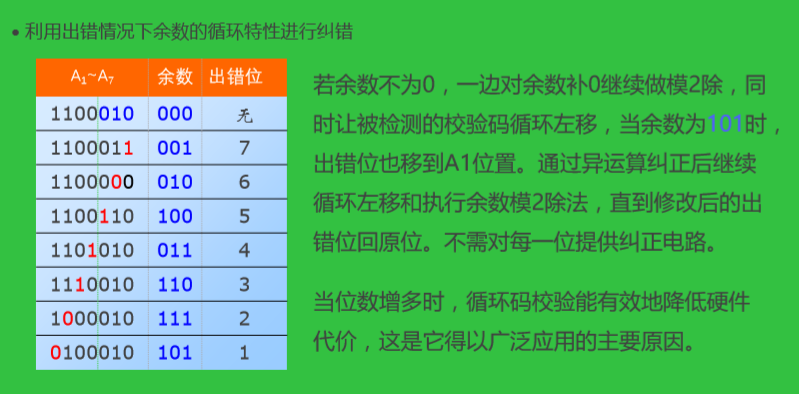
D、对不为0余数继续进行模2除运算应使余数循环。
2、模2除运算
*模2运算规则
1)加/减运算(异或运算,加不进位,减不借位)
0±0=0,0±1=1,1±0=1,1±1=0
2)模二除法
按模2减,求部分余数,不借位
3)上商原则
a.部分余数首位为1时,商为1,减除数
b.部分余数首位为0时,商为0,减0;
c.当部分余数的位数小于除数的位数时,该余数即为最后余数。

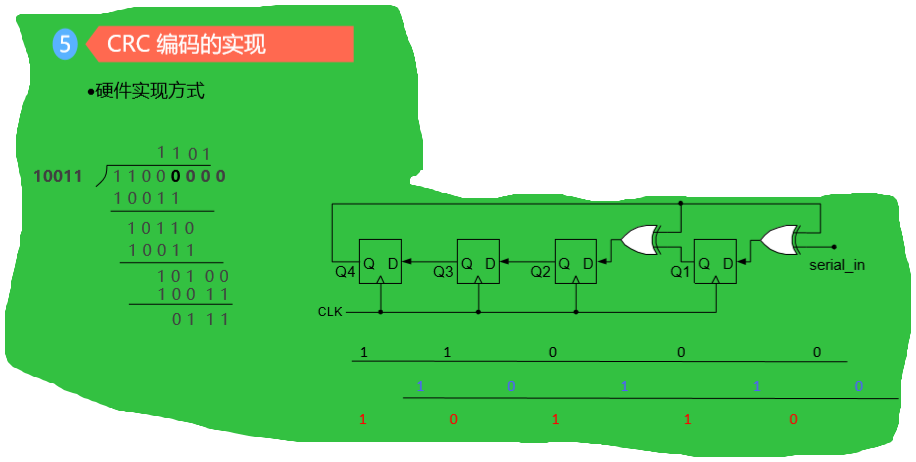
3、CRC编码方法
1)根据待检验信息的长度k,按照k+r≤2的r次方-1,确定校验位r的位数
如对4位信息1100进行CRC编码,根据4+r≤2的r次方-1,得r最小为3
2)根据r和生成多项式得选择原则,选择位数为r+1得生成多项式G(X)=1011
3)进行下列变化

即:将待校验得二进制信息Q(X)逻辑左移r位,得到Q(X)'
4)对Q(X)'按模2运算法则除G(X),求CRC编码中的r位检验信息
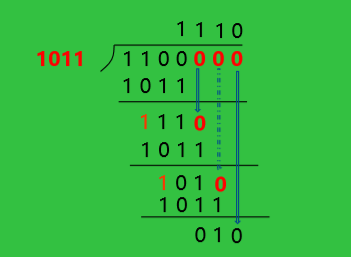
5)用得到的余数替换Q(X)'的最后r位即可得到CRC编码

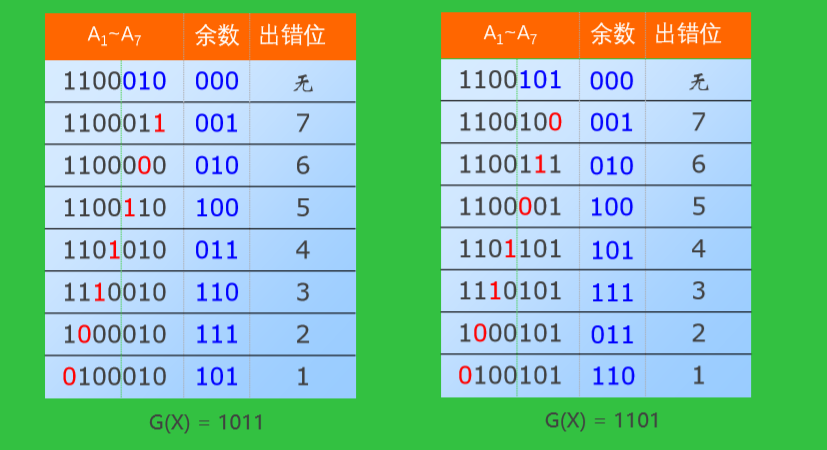
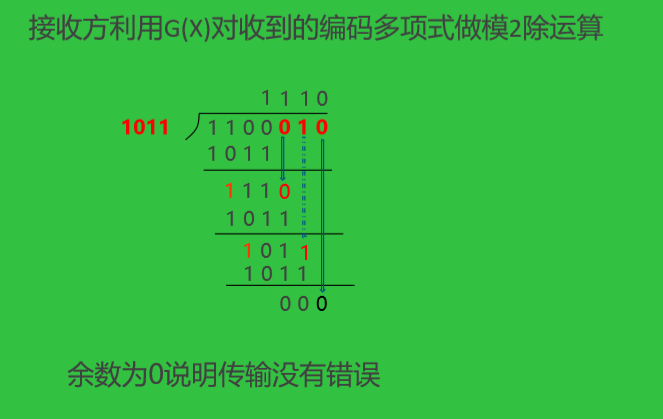
4、CRC的检错与纠错
接收方利用G(x)对收到的编码多项式做模2除运算
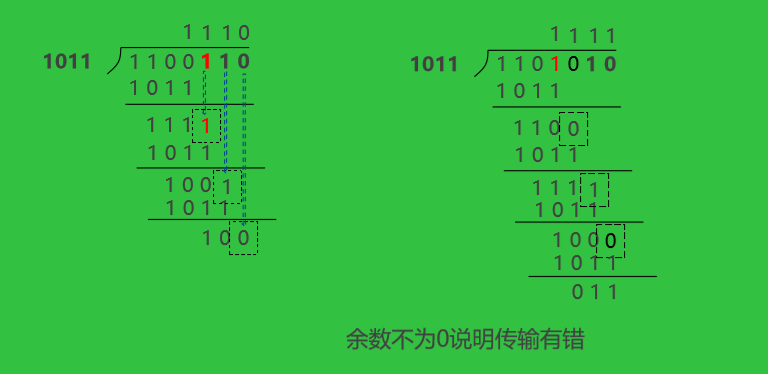
(7,4)编码不同数位出错对应的余数