圆上的点划分三角形问题

问题描述

一个圆上有 3n 个点, 一共有多少种不同方式将这些点连接成 n 个没有共同顶点且不相交的三角形?
n = 5 时的结果是多少?

分析

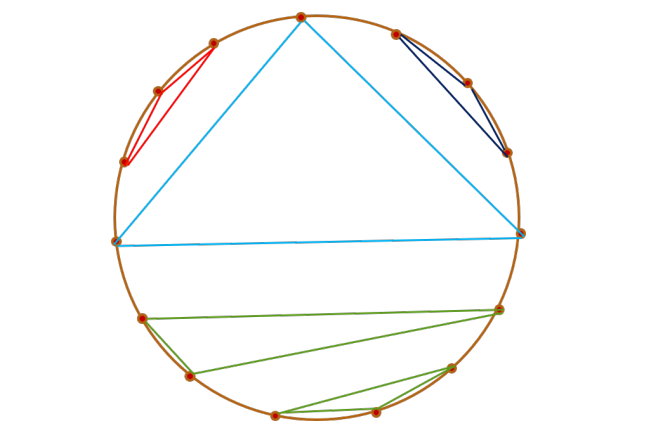
这个问题的解法就是分治加递归.

如下图所示:

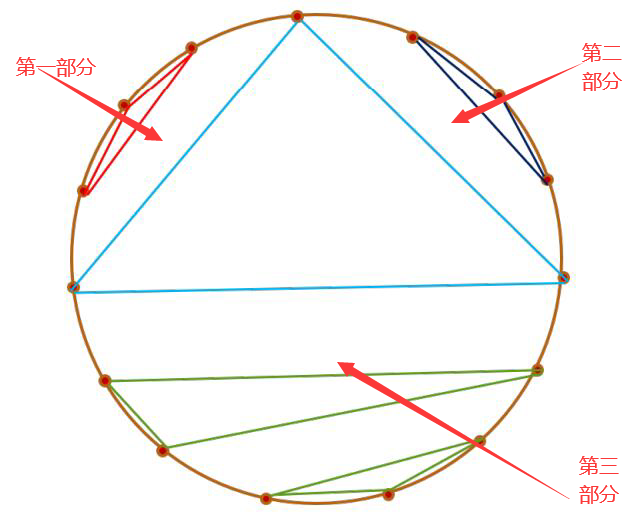
以中间的蓝色的三角形的三条边为分割线, 我们可以把圆看成三个部分, 我们只分别求出三个部分的各自的不同的三角形的数量, 然后相乘, 就可以得到该情况下的不同的三角形的种数, 到这里我们用到了分治. 然后我们只需要一个二重循环, 然后递归求解即可.

算法描述:

for (int i = 0; i <= n-1; i++)
{
    for (int j = 0; j <= n-1-i; j++)
    {
        //combo of three parts
        count += Count (i)*Count (j)*Count (n-1-i-j);
    }
}

i 代表的是第一部分, j 代表的是第二部分, (n - 1 - i - j) 代表的是第三部分. 因此, 通过这个二重循环, 即可遍历所有的情况, 然后将每一次的结果相加就是最后的结果.

代码

注: 这是老师给的代码

#include <stdio.h>

int Count (int n)
{
    int count=0;

    if (n == 0)
        return (1);

    for (int i = 0; i <= n-1; i++)
    {
        for (int j = 0; j <= n-1-i; j++)
        {
            //combo of three parts
            count += Count (i)*Count (j)*Count (n-1-i-j);
        }
    }
    return (count);
}

int main ()
{
    int i = 5;

    printf ("count for %d is %d
", i, Count (i));
}

运行结果:

初版似乎有误的代码:

#include <stdio.h>

int count (int n)
{
    int sum =0;
    
    if (n == 0)
        return (1);
        
    for (int i = 0; i < n; i++)
        sum += count (i)* count (n - i - 1);
        
    return (sum);
}

int main ()
{
    int i;
    
    for (i = 1; i < 11; i++)
        printf ("%d is %d
", i, count (i));
}