leetcode 105. Construct Binary Tree from Preorder and Inorder Traversal

递归解法：

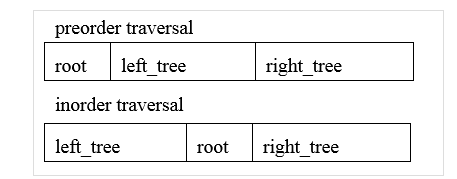
从先序遍历中得到树的根节点，从中序遍历中得到左右数的组成节点。

class Solution {
public:
      TreeNode *creTree(vector<int> preorder, int i,int j, vector<int> inorder,int m, int n)
        {
         
         // cout<<i<<"  "<<j<<endl;
          if(i>j&& m>n)
          {
               return NULL;
          }
             
        
       //得到根节点
       TreeNode * t=new TreeNode(preorder[i]);
    
          int k;
        for( k=m;k<n;k++)
            if(preorder[i]==inorder[k])
                break;

       //分开左右子树
       //这里是 i+k-m, 不是i+k, 因为k是在整个序列中的位置，而不是相对于m的位置
        t->left=creTree(preorder,i+1, i+k-m,inorder, m,k-1);
        
        t->right=creTree(preorder, i+k-m+1, j,inorder, k+1, n );
          return t;
        }
    
    
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0)
            return NULL;

        //cout<<* preorder.begin()<<endl;
        //cout<< * preorder.end()<<endl;
      //  if(preorder.begin()==preorder.end()-1)
        //    cout<<"ok"<<endl;
        return creTree(preorder,  0,  preorder.size()-1,  inorder, 0, inorder.size()-1);
       
    }
};

　更好理解的解法：

public TreeNode build(int[] preorder, int[] inorder, int preIndex,
            int startInIndex, int endInIndex) {
        if (endInIndex < startInIndex) {
            return null;
        }
        TreeNode node = new TreeNode(preorder[preIndex]);

        // the index of current node in inorder
        int index = getIndexInInorder(inorder, preorder[preIndex]);
        int lenL = index - startInIndex;
        int lenR = endInIndex - startInIndex - lenL;

        if (lenL > 0) {
            node.left = build(preorder, inorder, preIndex + 1, startInIndex,
                    index - 1);
        }
        if (lenR > 0) {
            node.right = build(preorder, inorder, preIndex + lenL + 1,
                    index + 1, endInIndex);
        }

        return node;
    }

　　

public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || preorder.length == 0) {
            return null;
        }
        if (inorder == null || inorder.length == 0) {
            return null;
        }

        if (preorder.length != inorder.length) {
            return null;
        }

        return build(preorder, inorder, 0, 0, inorder.length - 1);
    }