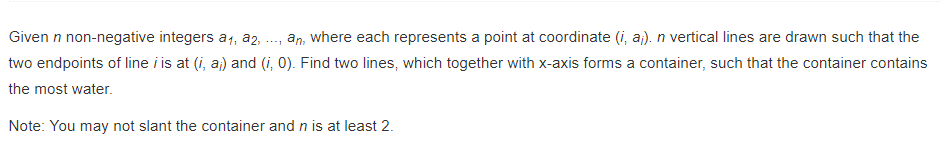
first, i use exhausitive search. however, it will exceed the time limit.
int maxArea(vector<int>& height) { int n=height.size(); int max=0; int s; for(int i=0;i<n;i++) for(int j=i+1;j<n;j++) { //cout<< i<<endl; //cout<<j<<endl; //cout<<n<<endl; int a=min(height[i],height[j]); cout<<a<<endl; s=(j-i)*a; if(s>max) max=s; } return max; }
the time speed is O(n^2)
then, i change the strategy. for impove the speed, I will search the vector from two direction. From the left to right and from right to left, until all the numbers has been checked.
int maxArea(vector<int> & height) { int n=height.size(); int max=0; int s; for(int i=0,j=n-1;i<j;) { s=(j-i)*min(height[i],height[j]); cout<< i<<endl; cout<<j<<endl; if(s>max) max=s; if(height[i]>height[j]) j--; else i++; } return max; }
the intuition behind this approach is that we want to find the biggest two line to construct the container. because the area is decided by the shorter line. To maximize the area, we need to consider the area between the lines of larger lengths. if we try to move the pointer at the longer line inwards, we won't gain any increase in area, since it is limited by the short line.O(n)
if left > right, it means that we should find a biger left.
if left <right, it means that we should find a biger left.