平面上的最接近点对

题目描述

给定平面上 nn 个点，找出其中的一对点的距离，使得在这 nn 个点的所有点对中，该距离为所有点对中最小的。

输入格式

第一行一个整数 nn，表示点的个数。

接下来 nn 行，每行两个实数 x,yx,y ，表示一个点的行坐标和列坐标。

输出格式

仅一行，一个实数，表示最短距离，四舍五入保留 44 位小数。

输入输出样例

输入 复制

3
1 1
1 2
2 2

输出 复制

1.0000

说明/提示

数据规模与约定

对于 100\%100% 的数据，保证 1 ≤ n ≤ 10^41≤n≤104，0 ≤ x, y ≤ 10^9，0≤x,y≤109，小数点后的数字个数不超过 66。

分治法求解

分解

  对所有的点按照 xx 坐标(或者 yy )从小到大排序(排序方法时间复杂度 O(nlogn))O(nlogn))。根据下标进行分割，使得点集分为两个集合。

解决

  递归的寻找两个集合中的最近点对。取两个集合最近点对中的最小值 min(dis_{left},dis_{right})min(disleft​,disright​)

合并

  最近距离不一定存在于两个集合中，可能一个点在集合 A，一个点在集合 B，而这两点间距离小于 disdis。
  其中如何合并是关键。根据递归的方法可以计算出划分的两个子集中所有点对的最小距离 disleft,disright，再比较两者取最小值，即 dis=min(dis_{left},dis_{right}) 。那么一个点在集合 A，一个在集合 B中的情况，可以针对此情况，用之前分解的标准值，即按照 x 坐标(或者 y)从小到大排序后的中间点的 x 坐标作为 mid。划分一个 [mid-dis,mid+dis] 区域，如果存在最小距离点对，必定存在这个区域中。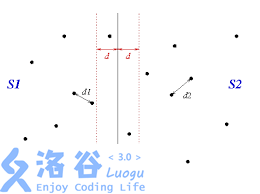

  之后只需要根据左边区域 [mid-dis,mid][mid−dis,mid] 的点来遍历右边区域 [mid,mid+dis][mid,mid+dis] 的点，即可找到是否存在小于 disdis 距离的点对。
  但是存在一个最坏情况，即通过左右两个区域计算得到的 disdis 距离来划分的第三区域可能包含集合所有的点，这时候进行遍历查找，时间复杂度仍然和 brute forcebruteforce 方法相同，都为O(n^2)O(n2)。因此需要对此进行深一步的考虑。

  1985年 Preparata 和 Shamos 在给出该问题的一个分治算法并且还具体分析了在 [mid-dis,mid+dis][mid−dis,mid+dis] 区域中出现的情况，若 (p,q)是 Q的最近点对，p 在带域左半部分，则 q 点必在下图所示的 2∗2δ 长方形上，而在该长方形上，最多只能由右边点集的6个点。每个点对之间的距离不小于δ。

 

此结论很好证明，通过在 δ∗2δ 上以 划成 66 个小长方形 

  用反证法来证明，假设存在大于6个点，则必有一个或多个小长方形存在两个及以上点，而小长方形的最长距离是为对角线长度，为：。最长距离都小于δ，与之前的条件不符合，故最多有6个点。借此，可以将可能的线性时间缩小到常数级，大大提高了平均时间复杂度。

时间复杂度

  在分解和合并时，可能存在按照x轴、y轴进行排序的预处理O(nlogn)，该问题在解决阶段只做提取的操作为Θ(n)，递推式为：

  计算后得到整体时间复杂度为:O(nlogn)。

代码

#include<bits/stdc++.h>
using namespace std;
struct point
{
    double x,y;
}p[200010];
int n,temp[200010];
bool cmp(const point &A,const point &B)
{
    if(A.x==B.x)
        return A.y<B.y;
    else
        return A.x<B.x;
}
bool cmps(const int &a,const int &b)
{
    return p[a].y<p[b].y;
}
double distance(int i,int j)
{
    return sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
}
double merge(int left,int right)
{
    double dis=2<<20;
    if(left==right)
        return dis;
    if(left+1==right)
        return distance(left,right);
    int mid=(left+right)>>1;
    double d1=merge(left,mid);
    double d2=merge(mid+1,right);
    dis=min(d1,d2);
    int k=0;
    for(int i=left;i<=right;i++)
        if(fabs(p[i].x-p[mid].x)<=dis)
            temp[k++]=i;
    sort(temp,temp+k,cmps);
    for(int i=0;i<k;i++)
        for(int j=i+1;j<k&&p[temp[j]].y-p[temp[i]].y<dis;j++)
            dis=min(dis,distance(temp[i],temp[j]));
    return dis; 
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
        scanf("%lf %lf",&p[i].x,&p[i].y);
    sort(p,p+n,cmp);
    printf("%.4lf
",merge(0,n-1));
    return 0;
}

不用分治

#include <bits/stdc++.h>
using namespace std;
struct point{
    double x,y;
}p[100001];
double dist(point a,point b){
    return sqrt(pow(fabs(a.x-b.x),2)+pow(fabs(a.y-b.y),2));
}
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>p[i].x>>p[i].y;
    }
    double mindist=dist(p[1],p[2]);
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            if(dist(p[i],p[j])<mindist)
            mindist=dist(p[i],p[j]);
        }
　　}
　　cout<<fixed<<setprecision(4)<<mindist;
    return 0;
}