想要验证一个策略是否有效,突然想到不如先做一个很简单粗糙的小实验,看看一个股票今天涨得多是不是意味着明天上涨的可能性更大。
数据范围是2008年1月到2018年12月(2677天),上证和深证的所有股票(3826支)。
基本思路是画两组图:
1.前一天上涨(下跌)-0.1/-0.05/0/0.05/0.09以上的前提下,第二天这支股票上涨5%以上的可能性
2.前一天上涨(下跌)-0.1/-0.05/0/0.05/0.09以上的前提下,第二天这支股票上涨(>0)的可能性
其中-0.1以上相当于对照组,因为所有的股票肯定都在跌停以上。
1 import pandas as pd 2 import matplotlib.pyplot as plt 3 import numpy as np 4 # 这两行代码解决 plt 中文显示的问题 5 plt.rcParams['font.sans-serif'] = ['SimHei'] 6 plt.rcParams['axes.unicode_minus'] = False 7 8 datapath = 'D:MyInternexampleDailyStock\' 9 increase_rate = pd.read_pickle(datapath+'increase_rate.pkl') 10 numrange = [-0.1, -0.05, 0, 0.05, 0.09] 11 premise = () 12 prob1 = [] 13 for i in numrange: 14 condition1 = increase_rate.shift()>i 15 condition2 = increase_rate>=0.05 16 denominator = increase_rate[condition1].count().sum() 17 tomorrow_increase = increase_rate[condition1 & condition2] #第二天会上涨 18 numerator = tomorrow_increase.count().sum() 19 ans = numerator/denominator 20 prob1.append(ans) 21 22 prob2 = [] 23 for i in numrange: 24 condition1 = increase_rate.shift()>i 25 condition2 = increase_rate>0 26 denominator = increase_rate[condition1].count().sum() 27 tomorrow_increase = increase_rate[condition1 & condition2] #第二天会上涨 28 numerator = tomorrow_increase.count().sum() 29 ans = numerator/denominator 30 prob2.append(ans) 31 numrange = [str(i) for i in numrange] 32 # plt.bar(numrange, prob2) 33 bar_width = 0.3 # 条形宽度 34 index_1 = np.arange(len(numrange)) # 男生条形图的横坐标 35 index_2 = index_1 + bar_width # 女生条形图的横坐标 36 37 # 使用两次 bar 函数画出两组条形图 38 plt.bar(index_1, height=prob1, width=bar_width, color='b', label='当天涨幅大于0.05') 39 plt.bar(index_2, height=prob2, width=bar_width, color='g', label='当天涨幅大于0') 40 41 plt.legend() # 显示图例 42 plt.xticks(index_1 + bar_width/2, numrange) # 让横坐标轴刻度显示 numrange里的数, index_1 + bar_width/2 为横坐标轴刻度的位置 43 plt.ylabel('可能性') # 纵坐标轴标题 44 plt.title('相邻两天股票涨幅的相关性') # 图形标题 45 plt.show()import pandas as pd 46 import matplotlib.pyplot as plt 47 import numpy as np 48 # 这两行代码解决 plt 中文显示的问题 49 plt.rcParams['font.sans-serif'] = ['SimHei'] 50 plt.rcParams['axes.unicode_minus'] = False 51 52 datapath = 'D:MyInternexampleDailyStock\' 53 increase_rate = pd.read_pickle(datapath+'increase_rate.pkl') 54 numrange = [-0.1, -0.05, 0, 0.05, 0.09] 55 premise = () 56 prob1 = [] 57 for i in numrange: 58 condition1 = increase_rate.shift()>i 59 condition2 = increase_rate>=0.05 60 denominator = increase_rate[condition1].count().sum() 61 tomorrow_increase = increase_rate[condition1 & condition2] #第二天会上涨 62 numerator = tomorrow_increase.count().sum() 63 ans = numerator/denominator 64 prob1.append(ans) 65 66 prob2 = [] 67 for i in numrange: 68 condition1 = increase_rate.shift()>i 69 condition2 = increase_rate>0 70 denominator = increase_rate[condition1].count().sum() 71 tomorrow_increase = increase_rate[condition1 & condition2] #第二天会上涨 72 numerator = tomorrow_increase.count().sum() 73 ans = numerator/denominator 74 prob2.append(ans) 75 numrange = [str(i) for i in numrange] 76 # plt.bar(numrange, prob2) 77 bar_width = 0.3 # 条形宽度 78 index_1 = np.arange(len(numrange)) # 男生条形图的横坐标 79 index_2 = index_1 + bar_width # 女生条形图的横坐标 80 81 # 使用两次 bar 函数画出两组条形图 82 plt.bar(index_1, height=prob1, width=bar_width, color='b', label='当天涨幅大于0.05') 83 plt.bar(index_2, height=prob2, width=bar_width, color='g', label='当天涨幅大于0') 84 85 plt.legend() # 显示图例 86 plt.xticks(index_1 + bar_width/2, numrange) # 让横坐标轴刻度显示 numrange里的数, index_1 + bar_width/2 为横坐标轴刻度的位置 87 plt.ylabel('可能性') # 纵坐标轴标题 88 plt.title('相邻两天股票涨幅的相关性') # 图形标题 89 plt.show()
画出图来长这样:
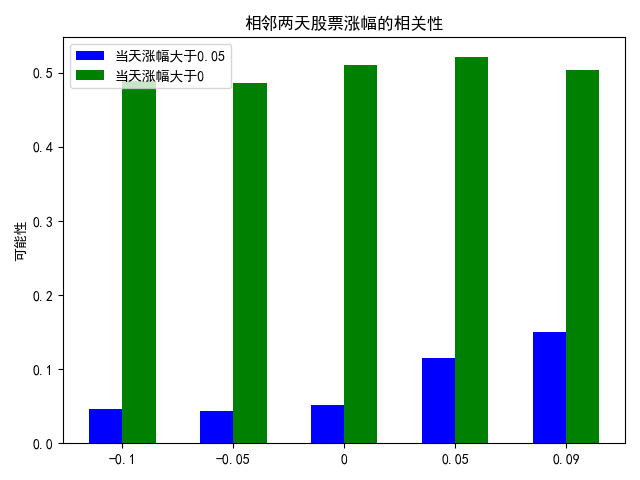
可见不管一只股票昨天涨没涨,涨了多少,都不能代表第二天该股票是否会上涨。平均下来股票上涨的概率都在50%左右。
但如果是关注涨幅大于5%的股票,前一天的涨幅就有了参考意义。从蓝色的柱子可以看出,前一天股票的涨幅越大,后一天该股票涨幅大于5%的可能性就越大,但最大也就14%左右。也就意味着,如果闭着眼追涨停的股票,第二天到收盘这只股票依然上涨的概率只有14%左右,这个概率还是很低的。
调整一下思路,第一天涨很多的股票,第二天是很有可能冲高回落的,这也是为什么我用(close-open)/open得到的结果只有14%。经过提示,决定尝试用第二天的(high-open)/open来考虑。
按照之前的想法,看一看前一天上涨(下跌)-0.1/-0.05/0/0.05/0.09以上的前提下,第二天这支股票最高上涨2%以上的可能性.
1 import pandas as pd 2 import matplotlib.pyplot as plt 3 import numpy as np 4 # 这两行代码解决 plt 中文显示的问题 5 plt.rcParams['font.sans-serif'] = ['SimHei'] 6 plt.rcParams['axes.unicode_minus'] = False 7 8 datapath = 'D:MyInternexampleDailyStock\' 9 increase_rate = pd.read_pickle(datapath+'increase_rate.pkl') 10 high_increase_rate = pd.read_pickle(datapath+'high_increase_rate.pkl') 11 numrange = [-0.1, -0.05, 0, 0.05, 0.095] 12 prob1 = [] 13 for i in numrange: 14 condition1 = increase_rate.shift()>i 15 condition2 = high_increase_rate>=0.02 16 denominator = increase_rate[condition1].count().sum() 17 tomorrow_increase = increase_rate[condition1 & condition2] #第二天会上涨 18 numerator = tomorrow_increase.count().sum() 19 ans = numerator/denominator 20 prob1.append(ans) 21 numrange = [str(i) for i in numrange] 22 plt.bar(numrange, prob1) 23 plt.title('相邻两天股票涨幅的相关性') # 图形标题 24 for a,b in zip(numrange,prob1): 25 plt.text(a, b+0.01, '%lf' %b, ha='center', va= 'bottom',fontsize=10) 26 plt.show()
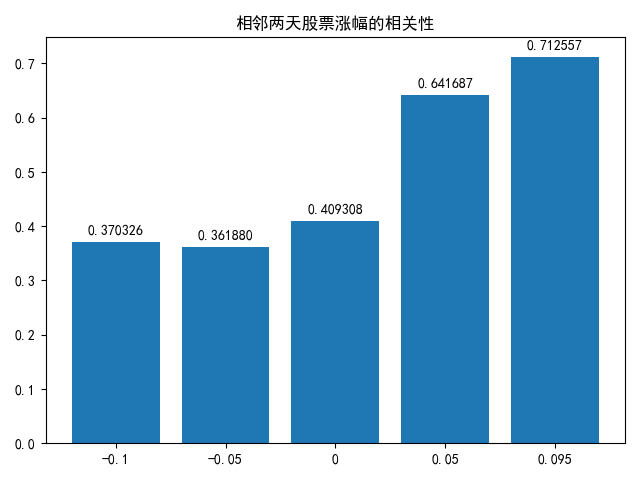
把2%调整成1%, 再画一张图:
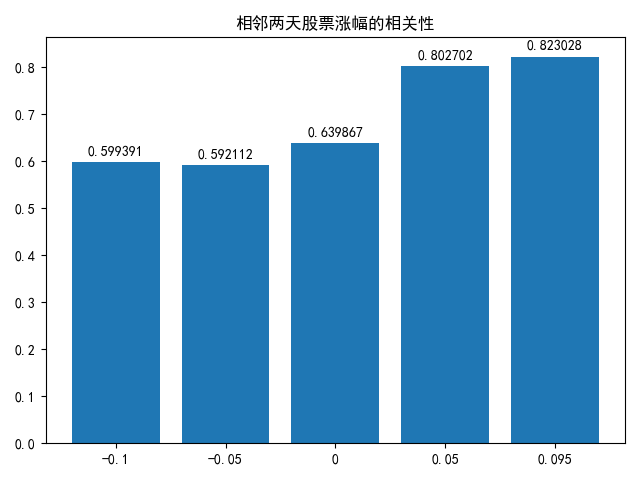
这个结果意味着,如果在收盘之前,随机选取一只今日上涨5%以上的股票,明天能等到它上涨1%的可能性高达80%!(如果是选一只涨停的股票这个概率并没有得到显著提高,所以5%就够用了)
但这个算法还有一点小问题。因为我的涨幅是用日内的(high-open)/open来算的,但实际我是在前一天收盘时买入,所以实际的收益率应该是用前一天的收盘价来计算。
再改进一下看看,存一个新的Pickle文件:
1 high_increase_new = (highp-closep.shift())/closep.shift()
得到结果:
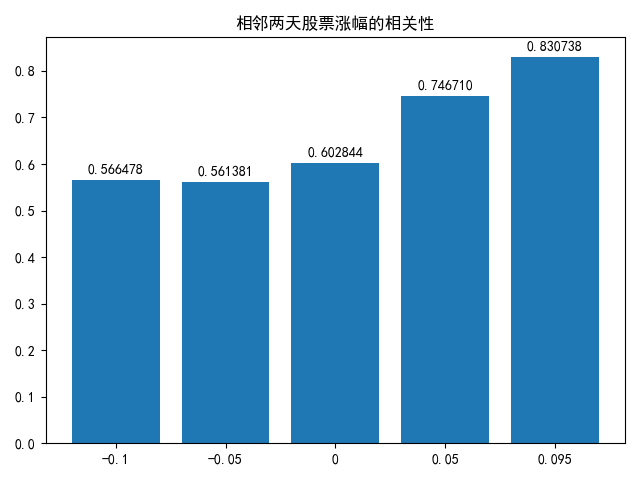
可以发现对于上涨5%的股票来说,这个概率有所下降,变为74.67%,但也很高了!如果能做到每天稳定盈利1%,一年也接近能翻11倍!!
当然,稳定的1%是不可能的,还需要得到一个在当天上涨5%的前提下,第二天最高涨幅的概率分布。(后续要得到更准确的结果,可能还要剔除涨停再算一次概率,因为会买不到)
补充:尝试了剔除涨停的股票,代码如下:
1 condition1 = increase_rate.shift()>0.05 2 condition2 = high_increase_rate>=0.01 3 condition3 = increase_rate.shift() <= 0.092 4 denominator = increase_rate[condition1 & condition3].count().sum() 5 tomorrow_increase = increase_rate[condition1 & condition2 & condition3] #第二天会上涨1% 6 numerator = tomorrow_increase.count().sum() 7 ans = numerator/denominator
发现概率并没有明显减少,算出来的结果是0.7271。
那么画一个直方图:
1 # 这两行代码解决 plt 中文显示的问题 2 plt.rcParams['font.sans-serif'] = ['SimHei'] 3 plt.rcParams['axes.unicode_minus'] = False 4 5 datapath = 'D:MyInternexampleDailyStock\' 6 increase_rate = pd.read_pickle(datapath+'increase_rate.pkl') 7 high_increase_rate = pd.read_pickle(datapath+'high_increase_new.pkl') 8 # numrange = [-0.1, -0.05, 0, 0.05, 0.095] 9 # prob1 = [] 10 condition1 = increase_rate.shift()>0.05 11 tmp = high_increase_rate[condition1] 12 sample = tmp.values.flatten() 13 sample = (pd.Series(sample)).dropna() 14 sample = sample.reset_index(drop=True) 15 sample.plot.hist(bins = 100, color = 'steelblue', edgecolor = 'black', label = '直方图') 16 print(sample.describe()) 17 # 绘制核密度图 18 # sample.plot.density(color = 'red', label = '核密度图') 19 # 添加x轴和y轴标签 20 plt.xlabel('涨幅') 21 plt.ylabel('频数') 22 # 添加标题 23 plt.title('头天上涨5%以上股票第二日涨幅分布') 24 # 显示图例 25 plt.legend() 26 # 显示图形 27 plt.show()
有一些小技巧,比如flatten()来把数组降维压扁。
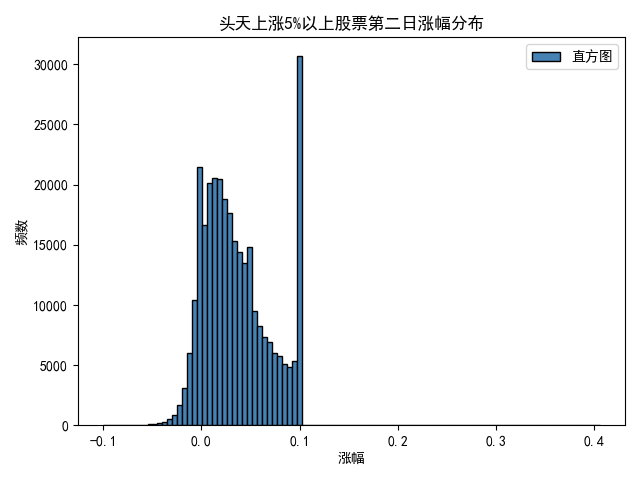
详情:
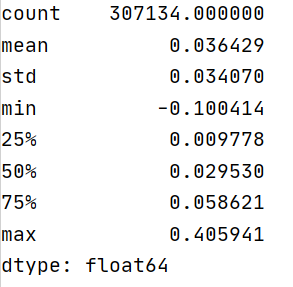
算了一下最高涨幅>=9.2%的比例是多少:
1 print(sample[sample>0.092].count()/sample.count())
结果是0.11746664322413018。
这个结果看起来虽然特别理想,但还有很多细节,比如因为数据的时间跨度很长,在看收益率的时候应当对冲指数,当然还要考虑交易成本等等。但我觉得结果也不会很差。还可以用样本外数据回测一下,看看用这种“临近收盘时从当天上涨5%的股票中随机选股,第二天只要盈利1%就卖掉”的方法无脑操作(还要设置一个止损线),收益表现怎样。