02C:垃圾炸弹
- 总时间限制:
- 1000ms
- 内存限制:
- 65536kB
- 描述
-
2018年俄罗斯世界杯(2018 FIFA World Cup)开踢啦!为了方便球迷观看比赛,莫斯科街道上很多路口都放置了的直播大屏幕,但是人群散去后总会在这些路口留下一堆垃圾。为此俄罗斯政府决定动用一种最新发明——“垃圾炸弹”。这种“炸弹”利用最先进的量子物理技术,爆炸后产生的冲击波可以完全清除波及范围内的所有垃圾,并且不会产生任何其他不良影响。炸弹爆炸后冲击波是以正方形方式扩散的,炸弹威力(扩散距离)以d给出,表示可以传播d条街道。
例如下图是一个d=1的“垃圾炸弹”爆炸后的波及范围。
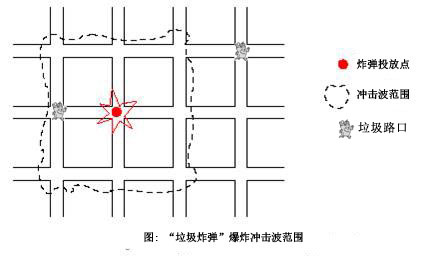
假设莫斯科的布局为严格的1025*1025的网格状,由于财政问题市政府只买得起一枚“垃圾炸弹”,希望你帮他们找到合适的投放地点,使得一次清除的垃圾总量最多(假设垃圾数量可以用一个非负整数表示,并且除设置大屏幕的路口以外的地点没有垃圾)。
- 输入
- 第一行给出“炸弹”威力d(1 <= d <= 50)。第二行给出一个数组n(1 <= n <= 20)表示设置了大屏幕(有垃圾)的路口数目。接下来n行每行给出三个数字x, y, i, 分别代表路口的坐标(x, y)以及垃圾数量i. 点坐标(x, y)保证是有效的(区间在0到1024之间),同一坐标只会给出一次。
- 输出
- 输出能清理垃圾最多的投放点数目,以及能够清除的垃圾总量。
- 样例输入
-
1 2 4 4 10 6 6 20
- 样例输出
-
1 30
1 #include<iostream> 2 using namespace std; 3 int x[21], y[21], w[21]; 4 int main(){ 5 int d, n; 6 cin>>d>>n; 7 int i, j; 8 for(i = 0; i < n; i++){ 9 cin>>x[i]>>y[i]>>w[i]; 10 } 11 int total = 0; 12 int ans = 0, count = 0; 13 for(i = 0; i < 1025; i++){ 14 for(j = 0; j < 1025; j++){ 15 total = 0; 16 for(int k = 0; k < n; k++){ 17 if(x[k]>=i-d&&x[k]<=i+d&&y[k]<=j+d&&y[k]>=j-d) 18 total += w[k]; 19 } 20 if(total > ans){ 21 ans = total; 22 count = 1; 23 } 24 else if(total==ans){ 25 count++; 26 } 27 } 28 } 29 cout<<count<<" "<<ans<<endl; 30 return 0; 31 }
备注:枚举也不都是无脑的orz 这道题就要想一想怎么个枚举法(枚举什么变量),如果用一个1025*1025的数组存整张图就傻了,因为一共最多就20个炸弹,而d最大能达到50.所以肯定是枚举坐标然后再来判断每个炸弹啊!