DFS
啦啦啦,再来水一波
先说思想吧!
背景:
深度优先搜索算法(英语:Depth-First-Search,简称DFS)是一种用于遍历或搜索树或图的算法。
————来自度娘
一、思想
DFS算法思想:一直往深处走,直到找到解或者走不下去为止
二、用途
由于时间复杂度过大一般不是正解,大部分情况是想不出题目正解,无奈之下写的暴力搜索或对拍时候用的,当然也有dfs的题,但是几乎不考。
三、实现过程
沿着树的深度遍历树的节点(不是树也没有关系啦,本蒟蒻图论菜的一批,依然学习了dfs),尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(n!)。
四、基本模版
int check() { if(满足条件) return 1; return 0; } void dfs(int step) { 判断边界 { 相应操作 } 尝试每一种可能 { 满足check条件 标记 继续下一步dfs(step+1) 恢复初始状态(回溯的时候要用到) }
会了模版,那就完结撒花了!

等等,显然我们并没有学会如何使用,那一起来看几个题目,熟悉一下。
四、题目(加深理解)
1、全排列问题
题目:给你n个字符串,把它们以此放入n个箱子中,输出全部排放方法。
思路:首先我们要检查箱子的状态(是否为空),将未放入的字符(未被标记的)放入,并进行标记
放入后要恢复到初始状态(回溯),到扫到了n+1个箱子时(边界处理),本次排列结束
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; int n,w; char s[100],re[100]; bool vis[100]; void dfs(int step) {//step为第几步,即第几个箱子 int i;//i为第i个字符 if(step==n+1) {//判断边界 for(i=1;i<=n;i++) printf("%c",re[i]); printf(" "); return ; } for(i=1;i<=n;i++) {//尝试每一种可能 if(vis[i]==0) {//满足check条件 (即:判断字符是否被标记) vis[i]=1;//标记 re[step]=s[i]; dfs(step+1);//继续下一步dfs(step+1) vis[i]=0;//恢复初始状态(回溯) } } return ; } int main() { scanf("%d",&w); for(int i=1;i<=n;i++){ memset(s,0,sizeof(s)); memset(vis,0,sizeof(vis)); scanf("%s",s+1); n=strlen(s+1); dfs(1); } return 0; }
2、Prime Ring Problem
题目:环由n个圆组成,如图所示。 将自然数1,2,...,n分别放入每个圆中,两个相邻圆中的数字之和应为素数。
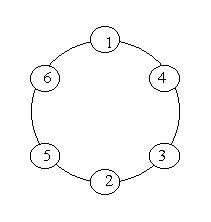
输入:n(0<n<20)
输出:输出格式如下所示。 每行代表环中的一系列圆圈数,从1开始顺时针和逆时针开始。 数字的顺序必须满足上述要求。 按字典顺序打印解决方案。
(输入时是要保证可以一直输入,看看代码就可以了)
样例:

思路:此题思路与全排列思路差不多,只是判断条件比较多,我们需要判断相邻两数之和是否为素数(注意最后一个字符会与1相加进行判断)
代码出来吧(皮卡丘)!

//Prime Ring Problem #include<bits/stdc++.h> using namespace std; int book[100],result[100],n; int prime(int n) {//判断是否为素数 if(n<=1) return 0; int i; for(i=2;i*i<=n;i++) { if(n%i==0) break; } if(i*i>n) return 1; return 0; } int check(int i,int step) {// 判断当前数字(i)是否能放入此位置 (step) if(book[i]==0&&prime(i+result[step-1])) {//此位置未被标记,且与前一个数的和为素数 if(step==n-1) {//判断是否是最后一步 if(!prime(i+result[0])) return 0;//判断最后一步与1的和是否为素数 } return 1; } return 0; } void dfs(int step) { if(step==n) {//边界处理 for(int a=0;a<n;a++) printf("%d ",result[a]); printf(" "); return ; } int i=2; for(i=2;i<=n;i++) { if(check(i,step)) {//满足check条件 book[i]=1;//标记 result[step]=i; dfs(step+1);//继续下一步dfs(step+1) book[i]=0;//恢复初始状态(回溯) } } return ; } int main() { int num=0; while(scanf("%d",&n)){//一直输入 num++; memset(result,0,sizeof(result)); memset(book,0,sizeof(book)); result[0]=1; printf("Case %d: ",num); dfs(1); printf(" "); } return 0; }
2019-07-12
3、油田问题(A - Oil Deposits )
题目:输入多个n行m列的矩阵,用00表示输入结束。找出有多少块石油区域,用“@”代表石油,假如两个“@”在横,竖或对角线上相邻(上,下,左,右,左上,左下,右上,右下),就说它们位于同一区域,对于每个输入,输出一个数表示有几个石油区域。
输入:n(1<=n<=100) m(1<=m<=100)
输出:对于每一个矩形区域,输出油藏的数量。
样例输入:
1 1
*
3 5
*@*@*
**@**
*@*@*
1 8
@@****@*
5 5
****@
*@@*@
*@**@
@@@*@
@@**@
0 0
样例输出:
0
1
2
2
思路:这个题其实比上一题简单,放在这里可能是因为它比较脱离模版(显然别人是这么排的),思路其实很简单了,若是求有多少块油(即:有多少@),扫一遍就好了,但题目要求,相邻的是同一个区域,求多少个区域,那就扫到每个油田我们都把与它相邻的八个点都扫一遍(若扫到的相邻的点也是油田,那就同样把他的相邻点也扫了,只记一次),注意的是扫到油田时,要将它标记并不将它恢复(回溯),否则我们将陷入死循环。 ( What? Why? ) 我们思考一下,当扫到一个油田(A)我们扫与它相邻的点,若其中还有油田(B),油田(A)也同样是与油田(B)相邻的,我们还要重新扫到油田(A),从而陷入死循环,所以我们不能回溯。
上代码!

//A - Oil Deposits #include<bits/stdc++.h> using namespace std; char a[105][105]; char dir[8][2]={{1,0},{-1,0},{1,1},{-1,-1},{0,1},{0,-1},{1,-1},{-1,1}}; int n,m,result; int check(int x,int y) {//检查是否有石油(@) if(x>=0&&x<=n&&y>=0&&y<=m&&a[x][y]=='@') return 1; return 0; } int dfs(int x,int y) { int i,xx,yy; if(check(x,y)) { a[x][y]='.';// 将找到的油田标记,不用恢复,会重复陷入死循环 for(i=0;i<8;i++) {//检查相邻的八个方向,若有油,将它标记,继续便利它的相邻方向 ,防止重复记录 xx=x+dir[i][0]; yy=y+dir[i][1]; dfs(xx,yy); } return 1; } return 0; } int main() { while(scanf("%d%d",&n,&m)) { if(n==0||m==0) break; result=0; memset(a,0,sizeof(a)); for(int i=1;i<=n;i++) scanf("%s",&a[i]); for(int i=1;i<=n;i++) {//对每个点都进行搜索 for(int j=0;j<m;j++) { if(dfs(i,j)) result++;//若发现油田结果+1 } } printf("%d ",result); } return 0; }
4、棋盘问题
题目:在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。
输入:输入含有多组测试数据。 每组数据的第一行是两个正整数,n k,用一个空格隔开,表示了将在一个n*n的矩阵内描述棋盘,以及摆放棋子的数目。 n <= 8 , k <= n 当为-1 -1时表示输入结束。 随后的n行描述了棋盘的形状:每行有n个字符,其中 ‘#’ 表示棋盘区域, ‘.’表示空白区域。
输出:对于每一组数据,给出一行输出,输出摆放的方案数目C (数据保证C<2^31)。
样例输入:
2 1 #. .# 4 4 ...# ..#. .#.. #... -1 -1
样例输出:
2
1
是不是很简单呐,没错,你已经掌握了dfs(深搜)的思路了,所以要先自己想一下,试着写一下代码,再看思路,题目很简单的。

思路:是不是都已经想出来了呢?(显然都已经A了)。只需要枚举每个棋子的位置,我们每次将一行放入棋子,放下一枚棋子时就在下一行放,用dir[]对放入的列进行标记,方便判断此列是否有放过棋子,就ok了。
代码!代码!麻利哄!
#include<bits/stdc++.h> using namespace std; int n,k,ans; char a[105][105]; int dir[105]; void dfs(int h,int k) { if(k==0) {//边界处理,若棋子放完,方案数+1 ans++; return ; } for(int i=h;i<n;i++) {//每次都从下一行开始搜避免了重复 for(int j=0;j<n;j++) { if(a[i][j]=='.'||dir[j]==1) continue;//dir[j]表示此列是否已经被占有 dir[j]=1;//标记 dfs(i+1,k-1);//搜下一行,棋子数量减少1 dir[j]=0;//恢复初始状态(回溯) } } } int main() { while(scanf("%d%d",&n,&k)) { if(n==-1&&k==-1) break; ans=0; memset(a,0,sizeof(a)); memset(dir,0,sizeof(dir)); for(int i=0;i<n;i++) { scanf("%s",a[i]); } dfs(0,k);//在第0行放第k个棋子 printf("%d ",ans); } return 0; }
(哇!我会深搜了!)是的,基本模版你已经掌握了,但是搜索是很考验代码能力的,所以需要勤加练习,多做题,增强码力!
