第一家面试公司:
滴滴打车(现场面试)
1.项目介绍(之后介绍项目问题)
2.给定一个节点,求这个节点在二叉树的哪层上
1 //给定节点在哪层上 2 int BitreeLevel(BiNode *root,char key) 3 { 4 if(root != NULL && !found)//一个条件不满足时就跳出 5 { 6 level++;//层数增加 7 if(root->data == key)//找到后标志 8 found = true; 9 else//没有找到继续找当前节点的左孩子或者右孩子 10 { 11 BitreeLevel(root->lchild,key); 12 BitreeLevel(root->rchild,key); 13 if(!found) 14 level--;//没有发现层数减1 15 //为什么这里层数减1? 16 //因为开始时层数加1才进入的下一层,即不管下一层是否都空都加1,然后再进入 17 //当没有找到后,返回 18 } 19 } 20 return level;//返回层数 21 }
第二家面试公司
IN我的生活(电话面试)
1.项目介绍(之后介绍项目问题)
2.recv函数返回值的考察
有关recv函数的相关知识:
函数原型:int recv( SOCKET s, char FAR *buf, int len, int flags );
不论是客户端还是服务器端应用程序都用recv函数从TCP连接的另一端接收数据。
该函数的:
第一个参数指定接收端套接字描述符;
第二个参数指明一个缓冲区,该缓冲区用来存放recv函数接收到的数据;
第三个参数指明buf的长度;
第四个参数一般置0。
这里只描述同步Socket的recv函数的执行流程。当应用程序调用recv函数时,recv先等待s的发送缓冲 中的数据被协议传送完毕,如果协议在传送s的发送缓冲中的数据时出现网络错误,那么recv函数返回SOCKET_ERROR,如果s的发送缓冲中没有数 据或者数据被协议成功发送完毕后,recv先检查套接字s的接收缓冲区,如果s接收缓冲区中没有数据或者协议正在接收数据,那么recv就一直等待,只到 协议把数据接收完毕。当协议把数据接收完毕,recv函数就把s的接收缓冲中的数据copy到buf中(注意协议接收到的数据可能大于buf的长度,所以 在这种情况下要调用几次recv函数才能把s的接收缓冲中的数据copy完。recv函数仅仅是copy数据,真正的接收数据是协议来完成的),recv函数返回其实际copy的字节数。如果recv在copy时出错,那么它返回SOCKET_ERROR;如果recv函数在等待协议接收数据时网络中断了,那么它返回0。
注意:在Unix系统下,如果recv函数在等待协议接收数据时网络断开了,那么调用recv的进程会接收到一个SIGPIPE信号,进程对该信号的默认处理是进程终止。
默认情况下socket是阻塞的。
阻塞与非阻塞recv返回值没有区别,都是:
<0 出错
=0 对方调用了close API来关闭连接
>0 接收到的数据大小,
特别地:返回值<0时并且(errno == EINTR || errno == EWOULDBLOCK || errno == EAGAIN)的情况下认为连接是正常的,继续接收。
只是阻塞模式下recv会一直阻塞直到接收到数据,非阻塞模式下如果没有数据就会返回,不会阻塞着读,因此需要循环读取)。
返回说明:
(1)成功执行时,返回接收到的字节数。
(2)若另一端已关闭连接则返回0,这种关闭是对方主动且正常的关闭
(3)失败返回-1,errno被设为以下的某个值
EAGAIN:套接字已标记为非阻塞,而接收操作被阻塞或者接收超时
EBADF:sock不是有效的描述词
ECONNREFUSE:远程主机阻绝网络连接
EFAULT:内存空间访问出错
EINTR:操作被信号中断
EINVAL:参数无效
ENOMEM:内存不足
ENOTCONN:与面向连接关联的套接字尚未被连接上
ENOTSOCK:sock索引的不是套接字
3.kmp算法的讲解以及编写
KMP字符串模式匹配通俗点说就是一种在一个字符串中定位另一个串的高效算法。简单匹配算法的时间复杂度为O(m*n);KMP匹配算法。可以证明它的时间复杂度为O(m+n).。
(1)普通的匹配算法
//暴力朴素的匹配思想 int BFMatch(char* pFather,char* pSOn) { int nFather=strlen(pFather); int nSon=strlen(pSon); int i=0,j; while(i<nFather) { j=0; while(pFather[i]==pSon[j]&&j<nSon) { i++; j++; } if(j==nSon) return i-nSon; i=i-j+1; //指针i回溯 } return -1; }
KMP算法实现的核心是next数组的计算
第一步:首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。

第二步:因为B与A不匹配,搜索词再往后移。

第三步:以此类推直到找到有一个字符和搜索词的第一个字符相同为止。

第四步:接着比较字符串和搜索词的下一个字符,还是相同。

第五步:直到字符串有一个字符,与搜索词对应的字符不相同为止

第六步:普通的BF算法会发生指针的回溯现象,这样做虽然可行,但是效率很低,因为你要把搜索位置移动到已经比较过的位置上,进行再一次的比较。

第七步:当空格与D不匹配时,你其实已经知道前面六个字符已经是”ABCDAB“。KMP算法的思想是,设法利用这个已知信息,不要把搜索位置移回已经比较过的位置,继续把它向后移动,这样来提高效率。

第八步:这是经过getNext函数所获取的next数组里面的数值,拥有了next数组,那么我们就可以很容易的解决字符串快速匹配问题。所以说KMP最核心的部分就是如何去求next数组。

第九步:已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,于是子串的指针跳转到SonID=next[SonID-1];的位置上。SonID=2;于是跳到搜索串C的位置。

第十步:之后因为空格与C也不匹配,搜索词还要继续进行跳转,这次依旧还是根据公式跳转
SonID=next[SonID-1];SonID=0;这时候又是空格和A进行比较,依旧不相等。
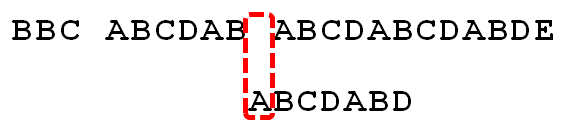
第十一步:那么父串指针移动到下一位,相同,两个串的指针就一起移动到下个位置

第十二步:逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。

第十三步:next数组的计算方法:
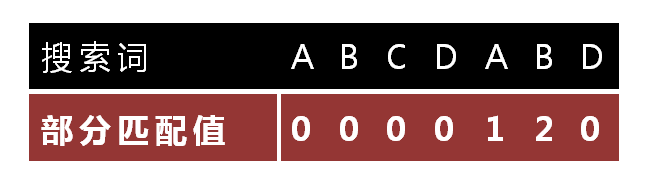
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
代码如下:
1 #include <iostream> 2 #include <string.h> 3 using namespace std; 4 void GetNext(char pStr[],int next[],int length) 5 { 6 if(pStr==NULL||next==NULL||length<=0) return; 7 int nLength=strlen(pStr); 8 next[0]=0; 9 for(int iValue=0,nld=1;nld<nLength;nld++) 10 { 11 while(iValue>0&&pStr[iValue]!=pStr[nld]) iValue=next[iValue-1]; 12 if(pStr[iValue]==pStr[nld]) 13 { 14 iValue++; 15 } 16 next[nld]=iValue; 17 } 18 } 19 //寻找子串中在父串中的首次出现的位置 20 int kmp(char* pSubStr,char* pStr,int next[]) 21 { 22 if(pSubStr==NULL||pStr==NULL||next==NULL) return; 23 int SubLength=strlen(pSubStr),SonLength=strlen(pStr); 24 GetNext(pStr,next,SonLength); 25 for(int SubID=0,SonID=0;SubID<SubLength;SubID++) 26 { 27 while(SonID>0&&pSubStr[SubID]!=pStr[SonID]) SonID=next[SonID-1]; 28 if(pStr[SonID]==pSubStr[SubID]) 29 { 30 SonID++; 31 } 32 if(SonID==SonLength) 33 return SubID-SonLength+1; 34 } 35 return -1; 36 } 37 int main() 38 { 39 //agctagcagctagctg 40 char Str[]="abcadcdfbcabca"; 41 char SonStr[]="cdf"; 42 int nlength=strlen(Str); 43 int next[100]; 44 //memset(next,0,sizeof(next)); 45 GetNext(Str,next,nlength); 46 cout<<kmp(Str,SonStr,next)<<endl; 47 system("pause"); 48 return 0; 49 }
转载一些大神们写的有关KMP相关文章:
http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
http://www.cnblogs.com/yjiyjige/p/3263858.html
http://blog.chinaunix.net/uid-27164517-id-3280128.html
第三家面试公司
58集团(现场面试)
一面:
1.自我介绍
2.项目介绍(之后会介绍)
3.工厂模式,单例模式,策略模式
这里我推荐大家看一个链接对于设计模式描述的很好:
http://www.jellythink.com/archives/878
二面:
1.自我介绍
2.多路复用I/O的考察:select,poll和epoll
如果说项目中存在网络编程一般会考到,所以挺重要的,这块知识点可深可浅,为什么说深,如果你很熟练的话,那么就聊一下各个模型是怎么运作的,聊聊epoll的底层实现(红黑树、回调机制和消息链表)为什么说浅,是时候该背背了。
会考察的题目一:select和epoll的区别
[1]select但进程只能打开1024个套接字[ulimit -a可以查询],epoll可以处理百万巨柄
[2]select只能处理可读可写及异常事件,epoll可以处理跟多类型的事件
[3]每一次调用select时都会进行一次内核态和用户态的拷贝,都需要重新填充待检测集合
[4]select返回的事件集合[就绪和为就绪的],采用轮询的方式来检测就绪事件,时间复杂度O(n)
[5]select采用LT处理模式,epoll有ET和EPOLLONESHOT[这两事件处理看书Linux高性能服务器编程]
[6]epoll采用回调的方式,内核检测到就绪文件描述符,触发回调函数[将文件描述符上对应的事件插入内核就绪事件队列
,内核在合适的时候将就绪事件队列中的内容拷贝到用户空间]事件复杂度O(1)
[7]epoll_wait返回到套接字都有事件
[8]epoll_wait未必高效,活动连接较多,回调函数被触发得过于频繁[不好],epoll_wait适用于连接数量多,但活动连接数较少的情况
建议扩展着说,不要给人感觉你是背的感觉。
会考察的题目二:select、poll1和epoll的区别
(1)select,poll实现需要自己不断轮询所有fd集合,直到设备就绪,期间可能要睡眠和唤醒多次交替。而epoll其实也需要调用epoll_wait不断轮询就绪链表,期间也可能多次睡眠和唤醒交替,但是它是设备就绪时,调用回调函数,把就绪fd放入就绪链表中,并唤醒在epoll_wait中进入睡眠的进程。虽然都要睡眠和交替,但是select和poll在“醒着”的时候要遍历整个fd集合,而epoll在“醒着”的时候只要判断一下就绪链表是否为空就行了,这节省了大量的CPU时间。这就是回调机制带来的性能提升。
(2)select,poll每次调用都要把fd集合从用户态往内核态拷贝一次,并且要把current往设备等待队列中挂一次,而epoll只要一次拷贝,而且把current往等待队列上挂也只挂一次(在epoll_wait的开始,注意这里的等待队列并不是设备等待队列,只是一个epoll内部定义的等待队列)。这也能节省不少的开销。
3.内存泄露问题:
http://blog.csdn.net/na_he/article/details/7429171
http://www.cnblogs.com/xitang/p/3645043.html
http://blog.csdn.net/zdy0_2004/article/details/50254283
4.大数据问题
问题描述:
有一个动物园,存在着一百万个动物,其中狮子是唯一的,其他种类动物每种两只,问如何找到这只唯一的狮子在哪?
解答:把每一个动物看做一个数的话,那么同种类的动物就是同一个数,我们根据两个相同的数抑或等于零,零任何数抑或都等于那个数的方式来确定那个唯一的值,
这样我们给动物们进行编号,进行每每抑或,那么最后就可以得出相应的动物了。