
数据结构 图
图的定义
A graph is made up of vertices/nodes and edges/lines that connect those vertices.
A graph may be undirected (meaning that there is no distinction between the two vertices associated with each bidirectional edge) or a graph may be directed (meaning that its edges are directed from one vertex to another but not necessarily in the other direction).
A graph may be weighted (by assigning a weight to each edge, which represent numerical values associated with that connection) or a graph may be unweighted (either all edges have unit weight 1 or all edges have the same constant weight).
图的相关术语
-
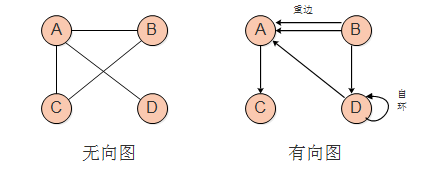
无向边:若顶点Vi和Vj之间的边没有方向,称这条边为无向边(Edge),用(Vi,Vj)来表示。 -
无向图(Undirected graphs):图中任意两个顶点的边都是无向边。 -
有向边:若从顶点Vi到Vj的边有方向,称这条边为有向边,也称为弧(Arc),用<Vi, Vj>来表示,其中Vi称为弧尾(Tail),Vj称为弧头(Head)。 -
有向图(Directed graphs):图中任意两个顶点的边都是有向边。 -
简单图:不存在自环(顶点到其自身的边)和重边(完全相同的边)的图 -
无向完全图:无向图中,任意两个顶点之间都存在边。 -
有向完全图:有向图中,任意两个顶点之间都存在方向相反的两条弧。
-
稀疏图;有很少条边或弧的图称为稀疏图,反之称为稠密图。 -
权(Weight):表示从图中一个顶点到另一个顶点的距离或耗费。 -
网:带有权重的图 -
度:与特定顶点相连接的边数; -
出度、入度:有向图中的概念,出度表示以此顶点为起点的边的数目,入度表示以此顶点为终点的边的数目; -
环:第一个顶点和最后一个顶点相同的路径; -
简单环:除去第一个顶点和最后一个顶点后没有重复顶点的环; -
连通图:任意两个顶点都相互连通的图; -
极大连通子图:包含竟可能多的顶点(必须是连通的),即找不到另外一个顶点,使得此顶点能够连接到此极大连通子图的任意一个顶点; -
连通分量:极大连通子图的数量; -
强连通图:此为有向图的概念,表示任意两个顶点a,b,使得a能够连接到b,b也能连接到a 的图; -
生成树:n个顶点,n-1条边,并且保证n个顶点相互连通(不存在环); -
最小生成树:此生成树的边的权重之和是所有生成树中最小的; -
AOV网(Activity On Vertex Network ):在有向图中若以顶点表示活动,有向边表示活动之间的先后关系 -
AOE网(Activity On Edge Network):在带权有向图中若以顶点表示事件,有向边表示活动,边上的权值表示该活动持续的时间
图的存储结构
由于图的结构比较复杂,任意两个顶点之间都可能存在关系,因此用简单的顺序存储来表示图是不可能,而若使用多重链表的方式(即一个数据域多个指针域的结点来表示),这将会出现严重的空间浪费或操作不便。这里总结一下常用的表示图的方法
邻接矩阵
邻接矩阵存储使用2个数组存储图的信息:1个一维数组存储顶点,一个二维数组存储边的信息,无向图是对接矩阵。
(无向图)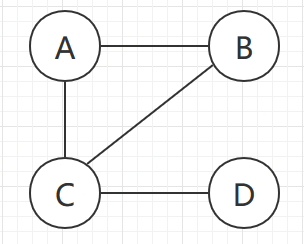
以上图为例,存放顶点的一维数组:
存放边的领接矩阵(adjacency matrix):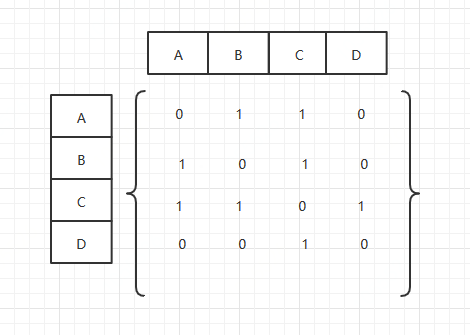
(带权有向图) 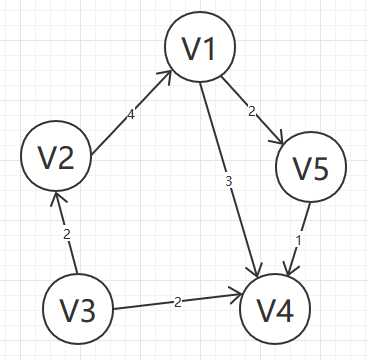
存放顶点的一维数组 
边数组 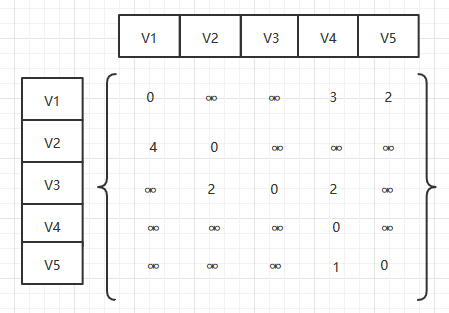
用⚮表示弧不存在,弧上面的数字代表权重。
邻接表
图的遍历
从图的某个顶点出发,遍历其余顶点,且使每个顶点仅被访问一次,叫做图的遍历。遍历通常分为:深度优先、广度优先。
深度优先搜索(DFS Deep first search)
遍历思想:基本思想:首先从图中某个顶点v0出发,访问此顶点,然后依次从v相邻的顶点出发深度优先遍历,直至图中所有与v路径相通的顶点都被访问了;若此时尚有顶点未被访问,则从中选一个顶点作为起始点,重复上述过程,直到所有的顶点都被访问。
广度优先搜索(Breadth First Search)
遍历思想:首先,从图的某个顶点v0出发,访问了v0之后,依次访问与v0相邻的未被访问的顶点,然后分别从这些顶点出发,广度优先遍历,直至所有的顶点都被访问完
图的知识太多了主要参考引用自Alent的博客