https://leetcode.com/problems/word-search-ii/description/
Given a 2D board and a list of words from the dictionary, find all words in the board.
Each word must be constructed from letters of sequentially adjacent cell, where "adjacent" cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
Example:
Input: words =["oath","pea","eat","rain"]and board = [ ['o','a','a','n'], ['e','t','a','e'], ['i','h','k','r'], ['i','f','l','v'] ] Output:["eat","oath"]
思路
给定一个字符矩阵,判断按指定规则能不能构成words中的词。可以利用DFS来从每个矩阵位置开始遍历,穷举所有的可能。当前字符不在任何word中时要去除掉以避免多余的计算。
- How do we instantly know the current character is invalid?
HashMap? - How do we instantly know what's the next valid character?
LinkedList? - But the next character can be chosen from a list of characters.
"Mutil-LinkedList"?
最高post的解答给出的方法是用tire,第一次碰到这个概念。搜了下,是单词查找树或键树,这种树形结构:
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同(这个貌似指的是同一层的子节点互不相同)。
比如:
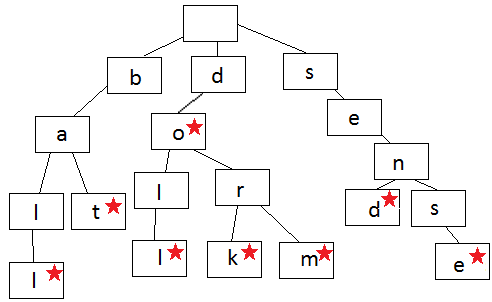
每一条边表示一个字符,如果结束,就用星号表示。在这个Trie结构里,我们有下面字符串,比如do, dork, dorm等,但是Trie里没有ba, 也没有sen,因为在a, 和n结尾,没有结束符号(星号)。
可以用它来保存一个字典,来查询改字典里是否有相应的词。也可以做智能提示,把用户已经搜索的词存在Trie里,每当用户输入一个词的时候,我们可以自动提示,比如当用户输入 ba, 我们会自动提示 bat 和 baii.
以上参考:https://www.cnblogs.com/yydcdut/p/3846441.html
现在回到算法题上来,根据给定的words我们可以构造一个tire树,然后去DFS字符矩阵时按照这个树去匹配。
代码
public List<String> findWords(char[][] board, String[] words) {
List<String> res = new ArrayList<>();
TrieNode root = buildTrie(words);
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
dfs (board, i, j, root, res);
}
}
return res;
}
public void dfs(char[][] board, int i, int j, TrieNode p, List<String> res) {
char c = board[i][j];
if (c == '#' || p.next[c - 'a'] == null) return; // 如果当前位置上的字符遍历过了,或者按当前字符为索引去下层找节点找不到时
p = p.next[c - 'a']; //
if (p.word != null) { // found one,如果p处存了整个word,也就是到了tire树的一个从上到下路径的最低端
res.add(p.word);
p.word = null; // de-duplicate
}
// dfs遍历以[i,j]处字符开始的所有可能的字符串,按照tire树判断字符串是否valid。遍历中只可能有两种情形:走到了null或者走到了存了word的末端
board[i][j] = '#'; //从i,j开始dfs时,因为在一个word里相同的cell不能重用所以要先置为#
if (i > 0) dfs(board, i - 1, j ,p, res);
if (j > 0) dfs(board, i, j - 1, p, res);
if (i < board.length - 1) dfs(board, i + 1, j, p, res);
if (j < board[0].length - 1) dfs(board, i, j + 1, p, res);
board[i][j] = c; //遍历结束后再置回来
}
public TrieNode buildTrie(String[] words) {
TrieNode root = new TrieNode();
for (String w : words) { // 遍历words中的所有word,
TrieNode p = root;
for (char c : w.toCharArray()) { // 遍历word中的所有字符,比如第一个是 “oath”
int i = c - 'a'; // 将字符与p中的索引一一对应起来(o, a, t, h)
if (p.next[i] == null) p.next[i] = new TrieNode(); //
p = p.next[i]; // 一趟for下来构造了竖直的 o-a-t-h 这样的tire树,只不过现在每个节点上的word是空的,
}
p.word = w; // p停在末位处(h),并且存储了整个word("oath")
}
return root;
}
class TrieNode { // 记录了当前节点中的word,以及下一层的所有节点,节点是根据数组索引来取,而数组索引可以根据字符直接得到,换句话说就是直接通过字符取节点
TrieNode[] next = new TrieNode[26]; // 每个节点下面一层最多有26个子节点,因为字母只有26个,这里通过索引来确定下层的字符,所以就不需要额外存储字符了
String word; // 这里的tire树还是有点不一样的
}
这里树的构造有点难理解,这里是定每个tire节点下面有26个节点,索引分别是a~z,然后初始全是null。如果每个字符是在当前word上时表明字符合法,那么将按照这个字符来索引到的节点初始化,只要使其不为null即可。以字符串 oath 为例,遍历其所有字符,从根节点开始,第一个字符是 o,现在知道根节点下层中的一个是字符o, 所以将根节点中的next数组在索引o处的TrieNode初始化,o的下个字符是a,那么将o的next数组中的o索引处的TrieNode初始化,一步步这样来,最后就构成了从根节点到索引为字符h的TrieNode的路径,路径上的节点不为空即可。最后在索引为h的TrieNode中存储整个word (“oath”)。