第三章 动态规划
1. 动态规划原理
这里要注意区别动态规划和分治的区别。下面来一些经典的例子。
2. 矩阵连乘
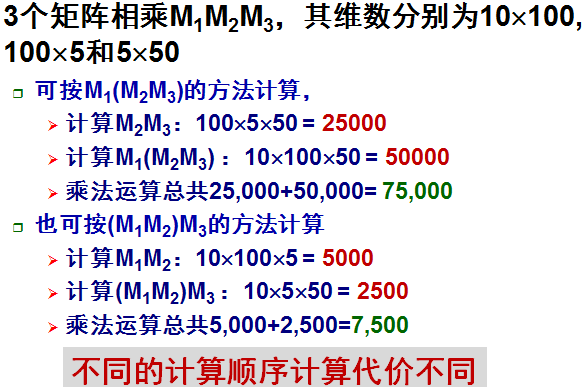
这里难点是怎么理解上面的那张表，这张表的意思就是对于m[1,5], (例如是矩阵A,B,C,D,E连乘：ABCDE ) 要考虑所有的断开的可能性(即所有的组合)，比如m[1,3]和m[3,5] (即对应于 "(AB)(CDE)" )。要在所有的断开的可能性中选乘法次数最小的话又得考虑m[1,3]和m[3,5]的情况。那么采取自底向上的方法，先考虑乘法组合只有一个的情况。第一遍先求m[1,1], m[2,2], m[3,3],m[4,4]和m[5,5], 由此可以计算出所有组合为2个的最小乘数m[1,2], m[2,3], m[3,4], m[4,5]。(比如m[1,2]的断开情况只有m[1,1]+m[2,2])。然后由上两遍的计算结果我们可以算出所有组合为3个的最小乘数：m[1,3], m[2,4], m[3,5]。(要注意到这里子问题是有重叠性的，因为在计算m[1,3]和m[2,4]时会重复利用到m[2,3]). 以此类推再计算所有组合为4个的最小乘数:m[1,4], m[2,5]。根据前4次的计算结果便可以计算出所有组合为5个的最小乘法次数了，这里5个矩阵在一起乘的只有m[1,5]，得出结果。之所说是自定向上的方法是因为是从底部开始往上算的，求出底部后才能去求顶部，途中的红色的斜线表示计算顺序，即第一遍要计算m[1,1], m[2,2], m[3,3],m[4,4]和m[5,5]，然后第二遍计算m[1,2], m[2,3], m[3,4], m[4,5]，以此类推，像个金字塔一样。
3. 钢条切割
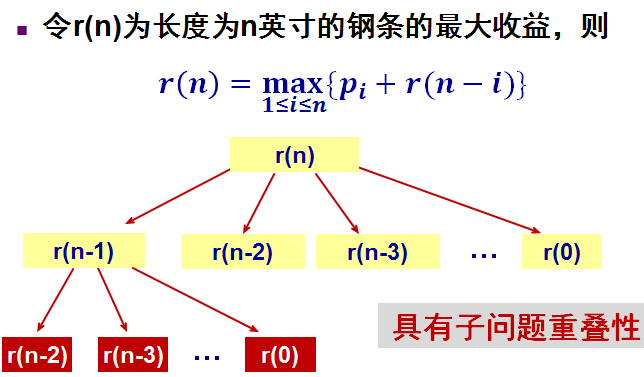
4. 最长公共子序列
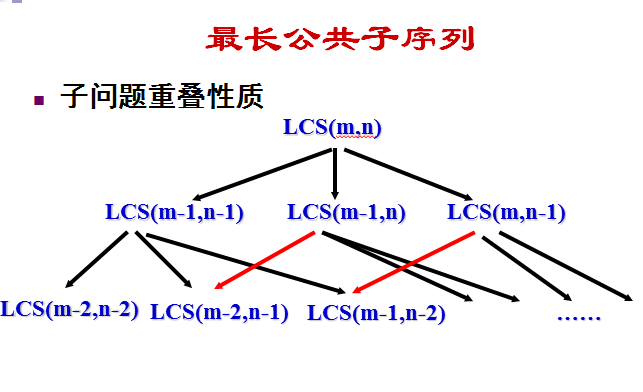
这里需要注意的一点是：子序列未必一定要是连续的。比如：BD就是ABCDE的一个子序列，不一定非得是BCD。
那么开始打表了(没记错的话，老师说过动态规划有时也被称为打表算法)，现在开始刷表喽！！！
这里的理解和矩阵连乘那个问题类似。按照上面的代码得出的结果是： 
这里竖排了序列ABCBDAB，横排了序列BDCABA。按
来，第一行和第一列都是0因为下标从0开始，从第二行第二列开始都是在执行如下判断：
如果X[i]=Y[i], 那么矩阵中对应的值LCS[i,j]=LCS[i-1,j-1]+1并添加左斜向上箭头，比如LCS[2,1], 因为X[2]=Y[1]=B, 所以LCS[2,1]=LCS[1][0]+1=0+1=1。如果X[i]不等于Y[i]，则取它上面和左边邻近的那两个值中的最大值，分别加向上箭头和向左箭头。比如LCS[3,1]，因为X[3]=C不等于Y[1]=B, 而LCS[2][1]=1, LCS[3,0]=0, 故取LCS[2][1]的值1并加向上箭头。
这样的一趟下来便可一求得两个序列的最大公共子序列。比如ABCBDAB和BDCABA, 他们最大公共子序列长度是4，从最右下角按照箭头开始找的出的公共子序列是：BCBA (只取数字发生增大的项)。
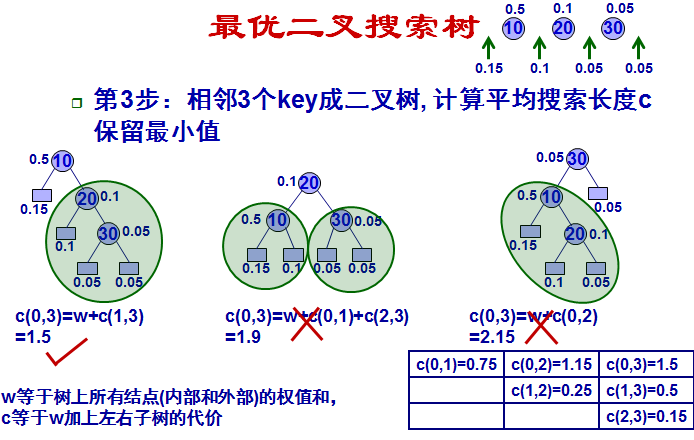
5. 最优二叉树搜索
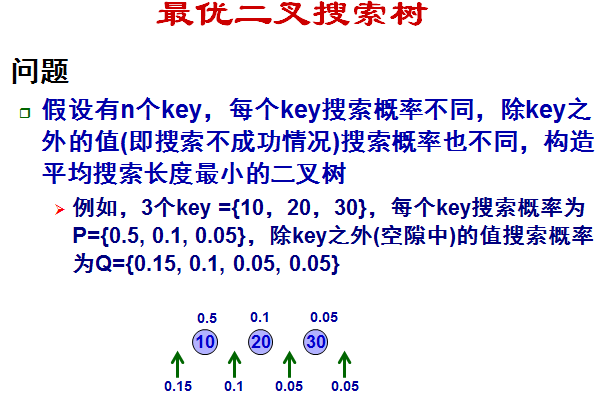
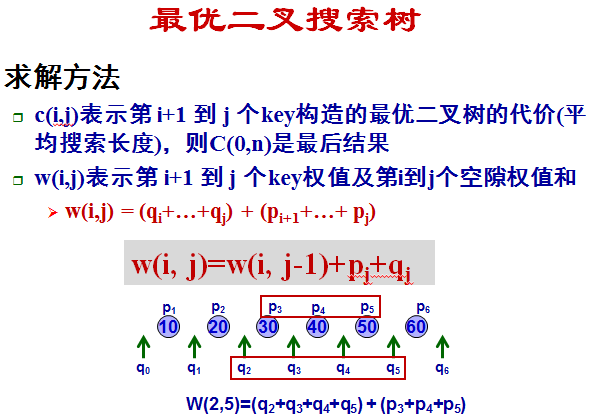
则可以推出：
，比如：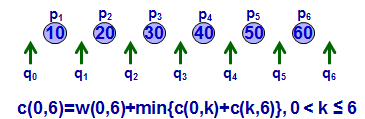
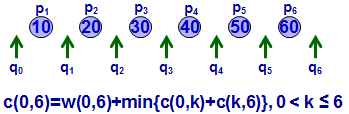
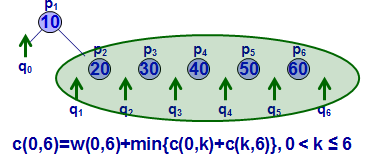
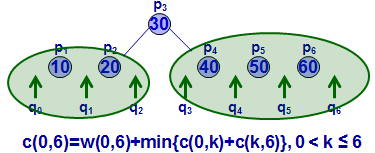
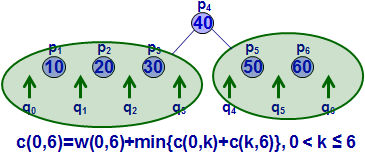
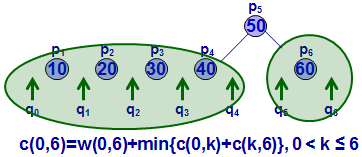
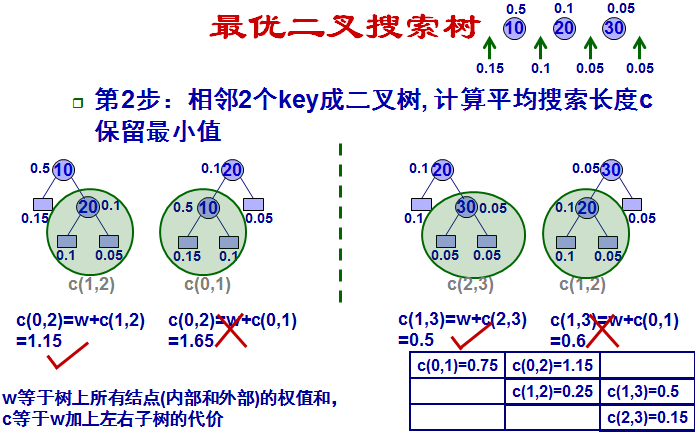
这里自己第二遍看得时候竟然突然不明白代价C(i,j)是怎么算的了。。。。 汗啊。这里的代价分两部分，一部分是书上所有节点的权值和，以C(0,1)为例，节点共3个，权值之和为0.75;问题在于第二部分，ppt定义为左右子树的代价，按照ppt来的话。它没有把叶节点算到子树里, 必须是包涵key的才行，比如计算C(0,2),按照定义会计算到C(0,1)和C(1,2),这是两个子树，自底向上的方法计算。
6. 流水作业调度问题
这个问题我写过了：动态规划——流水作业调度问题
7. 0/1背包问题
第二次看自己写的博客发现又看不明白。。。 感觉自己好笨啊。首先对于上面的伪代码，第一要做的是理解数学符号的具体意义是什么：min(wn-1,C)--其中C是背包的容量，wn--一个数学符号表示两个量：第n个物品的重量w, 记为wn. m(i,j)表示背包容量是j，可选物品是i,i+1，，，，n时问题的最优解。左上的那个图计算过程是自低向上的，意思就是：现在要求的是可选物品为1~n，背包容量为C时的最优解对吧？这个最优解应该是基于什么的呢？上面的证明已经证明出这个问题具有最优子结构，即可选物品为1~n，背包容量为C时的最优解应该基于可选物品为2~n时的最优解，但此时背包容量可能不再是C了，可能是C-w1，以此往下类推。接下来是怎么理解上面的那个伪代码：首先第一件事是将表的最底层初始化为0，m[n,0]~m[n,min(wn-1,C)]置为0，将最底层，m[n,wn]~m[n,C]置为第n个物品的价值vn。至于这里j为什么是从0到min(wn-1,C)呢（注意j表示的是背包的容量）？因为这个：
如果是C比较小，即wn比C大，意思就是第n个物品的重量比整个背包的容量还大，那么无需将此物品考虑到表中。为什么是min(wn-1,C)呢？因为考虑的是j小于wn的情况，不包括等于。再玩下看，到了这里：
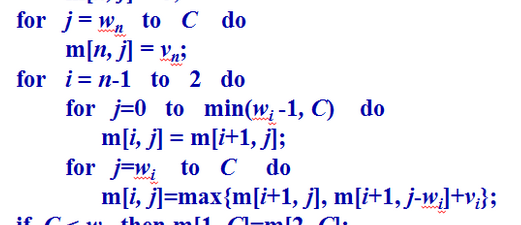
又不理解了，那么来假设把，如果现在计算的是表的倒数第二层，也就是i-1的时候的情况，这时候对于wi ，如果比j (记住j是此时背包剩余的容量) 大则将这层的m[i,j]全部置为m[i+1,j]，因为wi装入不了背包中，也有可能wi比j小，那么这个时候要考虑所有j>=wi的可能情况，从wi穷举到C，赋给倒数第二层的数组。从这里豁然开朗啦，对于表的每一层，穷举j从0到C，小于wi 的部分将m[i,j]置为m[i+1,j]，大于等于wi 的部分将m[i,j]置为max{m[i+1,j],m[i+1,j-]}以此构造表。终于高明白了，剩下就是实现这个算法了。
我个人关于动态规划的总结有2点：1. 将问题一层层的分解为规模逐渐减小的子问题。(前提是问题具有最优子结构的性质,否则分解为规模减小的子问题也没什么卵用)
2. 自底向上刷表计算。(或者递归求解什么的)