DS博客作业02--栈和队列

0.PTA得分截图

1.本周学习总结

1.1 栈

栈只能在一端进行插入和删除操作，后进先出

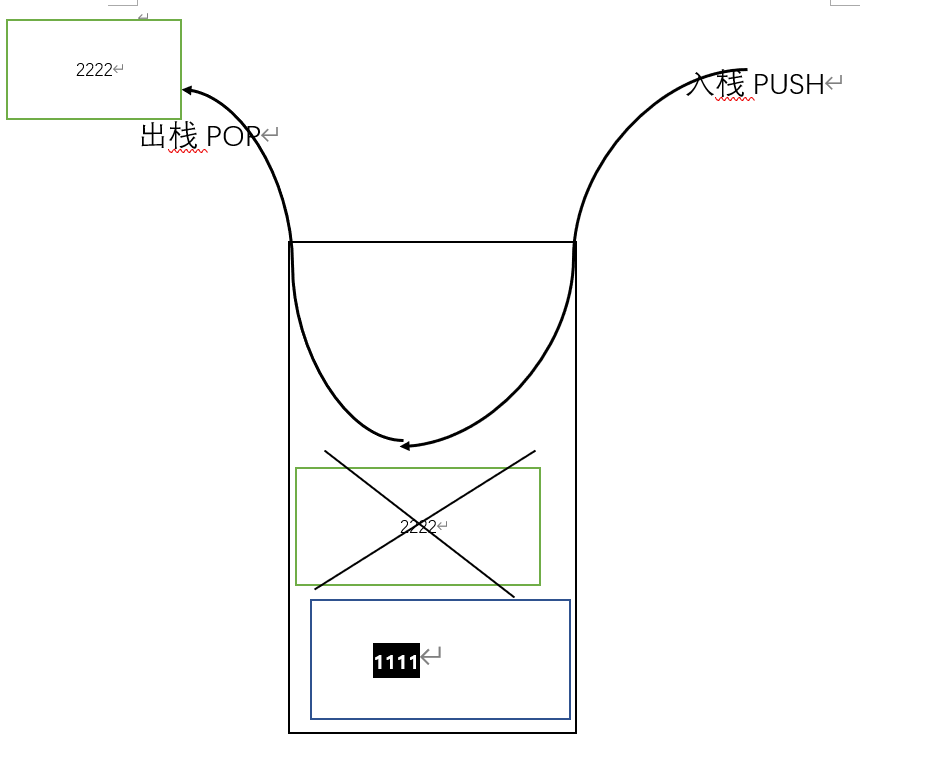
顺序栈的结构、操作函数

结构

#define MAXSIZE 100			//顺序栈存储空间的初始分配量
typedef struct
{
    ElemType data[MaxSize];			//存储栈元素
    int top;				//栈顶指针
}SqStack;

操作函数

初始化

void InitStack(SqStack *&s)
{
     s = (Stack)malloc(sizeof(struct SNode));
    s->Top = -1;
}

入栈

bool Push(SqStack *&S, ElementType X)
{

    if (S->Top == MaxSize-1 )
    {
        return false;
    }
    S->top++;  //要注意顺序
    S->Data[S->Top] = X;
    return true;
}

出栈

bool Pop(SqStack *&S,ElemTypr &e)
{

    if (S->top == -1)//栈空
    {
        return ERROR;
    }    
    e = S->Data[S->top];  
    S->top--;  
    return e;
}

判空和销毁栈

bool StackEmpty(SqStack *S)
{
     return S->top==-1;
}
void DesStack(SqStack *&S)
{
     free(s);
}

链栈的结构、操作函数

结构

typedef struct linknode
{ElemType data;//数据域
struct linknode *next;//指针域
} LinkSLNode;//链栈结点类型

初始化

void InitStack( LinkStNode&s)
{
s= (LinkStNode * )malloc( sizeof(LinkStNode));
s-> next=NULL；
}

入栈

void Push(LinkStNode * &.s, ElemType e)
{
LinkStNode * P;
p= (LinkStNode * )malloc(sizeof(LinkStNode));//新建结点p
p-> data=e;//存放元素e
p→>next=s→> next;//将P结点插人作为首结点
s-> next= p;
}

出栈

bool Pop(LinkStNode * &s, ElemType &.e)
{
LinkStNode * p;
if(s-> next= =NULL)//栈空的情况
return false;//返回假
p=s - > next;//p指向首结点
e=p- > data;//提取首结点值
s-> next=P - > next;//删除首结点
free(p);
return true;
}

判空和销毁栈

bool StackEmpty(SqStack *S)
{
     return S->top==-1;
}
void DesStack(SqStack *&S)
{
     free(s);
}

1.2 栈的应用，表达式

while (从exp读取字符ch,ch!=')
{
ch为数字:将后续的所有数字均依次存放到postexp中,并以字符井'标识数字申结束:
ch为左括号(:行此拓亏进找刊Opur中;
ch为右括号)':将Optr中出栈时遇到的第一个左括号'(以前的运算符依次出栈并
存放到postexp中，然后将左括号'('出栈;
ch为+'或'-:出栈运算符并存放到postexp中，直到栈空或者栈顶为'(，然后将ch进栈;
ch为*或/:出栈运算符并存放到postxp中，直到栈空或者栈顶为'('、十'或” -,然后将ch进栈;
}
若exp扫描完毕,则将Optr中的所有运算符依次出栈并存放到postexp中。

voidtrans(char *exp, char postexp[])//将算术表达式exp转换成后缀表达式postexp
{
char e;
SqStack* Optr;//定义运算符栈指针
InitStack(Optr);//初始化运算符栈
int i = 0;//i作为postexp的下标
while (*exp != '')//exp表达式未扫描完时循环
{
	switch (*exp)
	{
	case '('://判定为左括号
		Push(Optr, '('); //左据号进栈
		exp++;//继续扫描其他
		break;
	case')':
		Pop(Optr, e);//出栈e
		while (e != '(')//不为(时循环
		{
			postexp[i++] = e;//将e存敢到postexp中
			Pop(Optr, e);//继续出栈
		}
		exp++;//继续扫播其他字养//月定为加成减号
		break;
	case'+':
	case'-':
		while (!SuackEmpty(Optr))
		{
			GetTop(Optr, e);//联栈顶元素。
			if (e != '(')//e不是'('
			{
				postexp[i++] = e;//将e存放到postexp中
				Pop(Optr, e);
			}
			else
				break;
		}
		Push(Optr, *exp);//将'+'或'一'进栈
		exp++;//继续扫描其他字符
		break;

	case'*'://判定为*或/号
	case'/':
		while (!StackEmpty(Optr))//栈不空循环
		{
			GetTop(Optr, e);//取栈顶元素e
			if (e == '*' || e == '/')//将校顶'。或/'运算符出钱并存放
			{
				postexp[i++] = e;//将e存放到postexp中
				Pop(Optr, e);//出栈元索e
			}
			else
				break;//e为非'*'或/'运算符时退出循环
		}
		Push(Optr, *exp);//将'*'或/进栈

		exp++;//继续扫描其他字符
		break;
	delault://处理数字字符

		while (*exp >= '0' && *exp <= '9')//判定为数字字符
		{
			postexp[i++] = *exp;
			exp++;
		}
		postexp[i++] = '#';//用#标识一个数字申结束
	}
	while (!StckEmpty(Optr))//此时xp扫指完中，校不空时情环
	{
		Pop(Optr, e);//出栈元素e
		postexp[i++] = e;//将e存放到postexp中
	}
	postexp[i] = '';//给postexp表达式添加结束标识
	DestroyStack(Optr);//销毁栈
}

1.3 队列

队列允许在一端进行插入，在另一端进行删除，先进先出

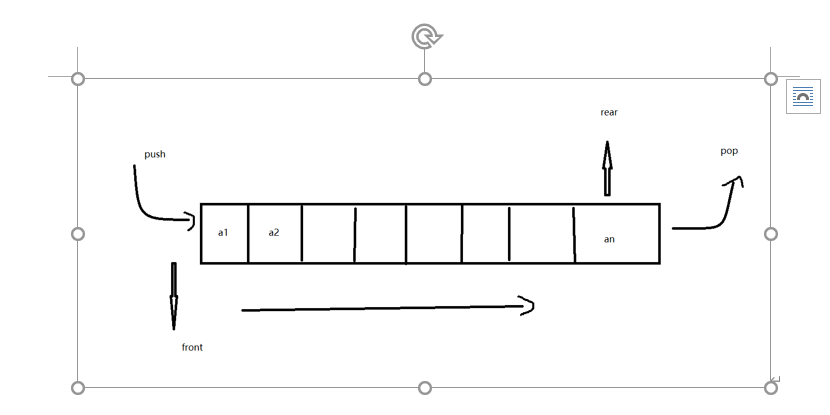
顺序队列的结构、操作函数

结构

typedef struct
{ElemType data[MaxSize] ;//存放队中元素
int front, rear;//队头和队尾指针
}SqQueue;//顺序队类型

初始化

void InitQueue( SqQueue * &.q)
{ q= (SqQueue * )malloc( sizeof(SqQueue));
q-> front=q-> rear=- 1;
}

入队列

bool enQueue(SqQueue * &q, ElemType e)
{ if (q-> rear== MaxSize- 1)//队满上溢出
return false;//返回假
q-> rear++;//队尾增1
q-> data[q-> rear]=e;//rear位置插入元素e
return true;//返回真
}

出队列

bool deQueue(SqQueue * &q, ElemType &e)
{ if (q-> front==q-> rear)//队空下溢出
            return false;
q->front++;
e=q -> data[q -> front];
return true;
}

队空和销毁队

void InitQueue(SqQueue * &q)
{
q= (SqQueue * malloc( sizeof(SqQueue));
q-> front=q-> rear=- 1;
}
void DestroyQueue(SqQueue * &q)
{
     free(q);
}

环形队列的结构、操作函数

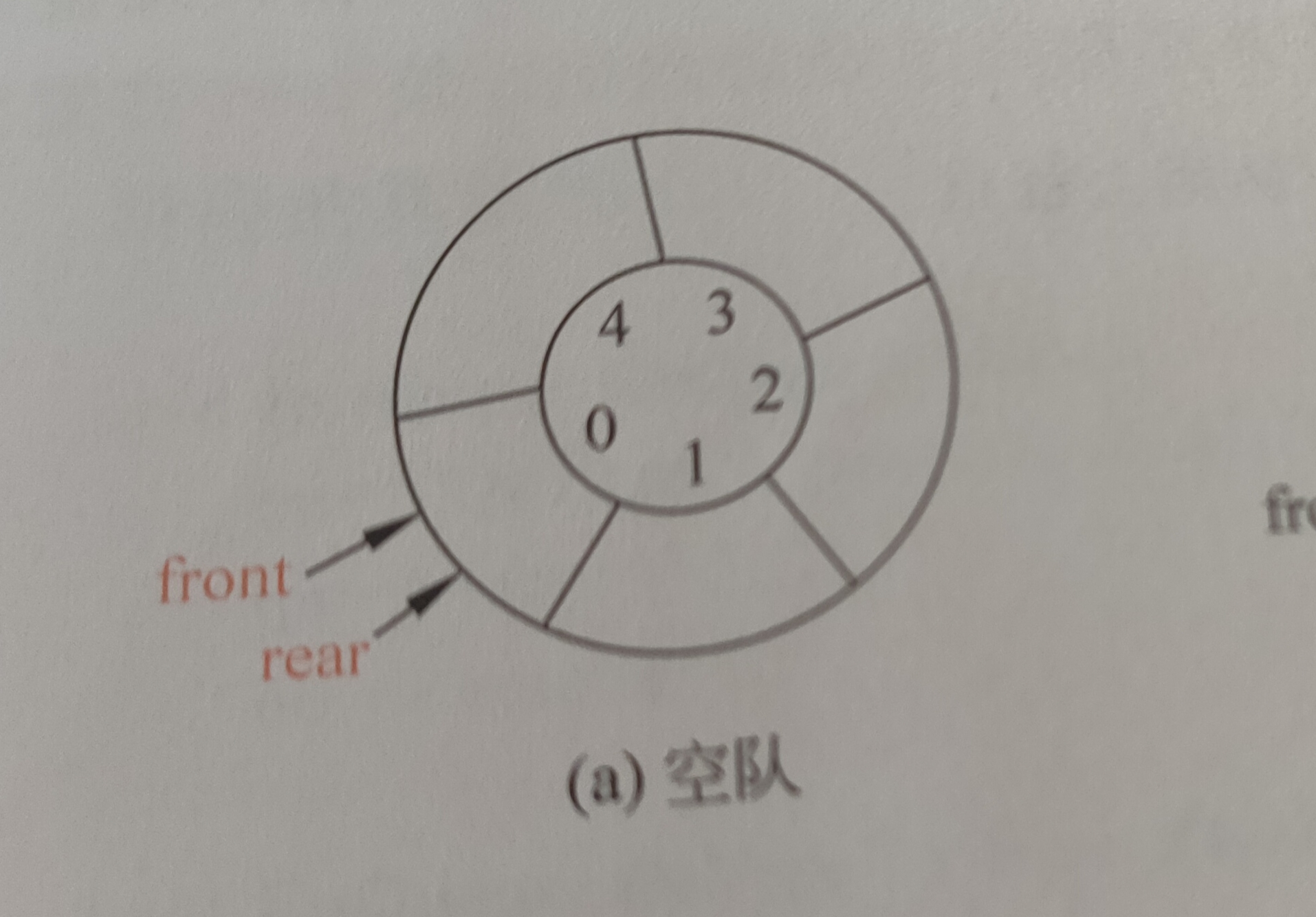
结构

typedef struct
{ElemType data[MaxSize] ;//存放队中元素
int front, rear;//队头和队尾指针
}SqQueue;

初始化

void InitQueue( SqQueue * &.q)
{ q= (SqQueue * )malloc( sizeof(SqQueue));
q-> front=q-> rear=0;
}

入队列

bool enQueue(SqQueue * &q, ElemType e)
{if ((q- rear+ 1)%MaxSize==q-> front)//队满 
           return false;
q->rear=(q-> rear十1) % MaxSize;
q->data[q→> rear]=e

return true;

出队列

bool deQueue(SqQueue * &q, ElemType &e)
{ if (q-> front==q-> rear)//队空下溢出
            return false;
q->front=（q->front+1)%MaxSize;
e=q -> data[q -> front];
return true;
}

队空和销毁队

void QueueEmpty(SqQueue * &q)
{

return(q-> front==q-> rear);
}
void DestroyQueue(SqQueue * &q)
{
     free(q);
}

链队列的结构、操作函数

结构

typedef struct qnode
{ElemType data;//存放元素
struct qnode * next;//下一个结点指针
} DatalNode;//链队数据结点的类

初始化

void InitQueue( LinkQuNde * &.q)
{ q= (LinkQuNde * )malloc( sizeof(LinkQuNde));
q-> front=q-> rear=NULL;
}

入队列

void enQueue(LinkQuNode * &q, ElemType e)
{
DataNode*p;
p= (DataNode * )malloc( sizeof( DataNode)); //创建 新结点
p-> data=e;
p-> next= NULL;
if (q-> rear== NULL)//若链队为空，则新结点既是队首结点又是队尾钻去
    q->front=q-> rear= P;
else//若链队不空
{ q-> rear-> next= P;//将结点p链到队尾,并将rear 指向它
q-> rear=p;
}
}

出队列

bool deQueue(LinkQuNode . &q. ElemType &e)
{
DataNode *t:
if(q-> rear== NULL)//原来队列为空
   return false;
t=q -> front;//t指向首结点
if (q-> front==q- > rear)
     q-> front=q-> rear= NULL;
else
   q> front=q-> front-> next;
e=t-> data;
free(t);
return true;

队空和销毁队

bool QueueEmpty(LinkQueue * &q)
{

return(q-> rear==NULL);
}
void DestroyQueue(LinkQuNode*&q)
{DataNode * pre=q > front, * p;//pre指向队首结点
if (pre!=NULL)
{
p=pre- > next;//p指向结点pre的后继结点
while (p!= NULL)//p不空循环
{free(pre) ;//释放pre结点
pre=p;P=P- > next;//pre、p同步后移
}
free(pre);//释放最后一个数据结点
}
free(q);//释放链队结点

队列应用,报数问题

void number(int n)
{
	int i; ElemType e;
	SqQueue* q;//环形队列指针q
	InitQueue(q);//初始化队列q
	for (i = 1; i <= n; i++)//构建初始序列
		enQueue(q, i);
	printf(”报数出列顺序:");
		while (!QueueEmpty(q))//队列不空循环
		{
			deQueue(q, e);//出队一个元素e
			printf("%d ", e)//输出元素编号
				if (!QueueEmpty(q))//队列不空
					deQueue(q, e);//出队一个元素e
			enQueue(q, e);//将刚出队的元素进队
		}
	printf("
");
	DestroyQueue(q);//销毁队列q
}

2.PTA实验作业

代码 https://gitee.com/fu-zhaoyang/codes/zk7prjd6q3v1s84cye5iu75

2.1 符号配对

2.1.1 解题思路及伪代码

初始化栈
for i 0 to exp.size（）
 if(是‘（’）
  入栈
 else if（是')')
   if(栈为空)return 
   取栈顶元素
   if(不是‘）’）
    配对不成功
   else
    配对成功；出栈；
  if(是‘{’）
   ......
if（表达式遍历完且栈为空）
return true
else if（栈不为空）
cout栈顶；
return false

2.1.2 总结解题所用的知识点

对栈的定义，初始化，入栈，出栈等操作
利用stack库，使得操作更快
对的各种情况的判断

2.2 银行业务队列简单模拟

2.2.1 解题思路及伪代码

for i=0 to n
       输入所有顾客编号
        遍历所有编号
       if x为偶数
          进入A队
        else
       进B队 
while (A,B全不空)
   输出两次A，一次B
if (A空)
    输出B剩余
else
    输出A剩余

2.2.2 总结解题所用的知识点

1.队列的创建，判空，入队，出队操作
2.对两个队列的判断，当A或B两个有一个队列为空就退出循环，然后单独输出剩余队列

3.阅读代码

3.1 题目及解题代码

最小栈
题目信息
设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。

class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {
        min_val = INT_MAX;
    }
     
    void push(int x) {
        if (x <= min_val) {
            st.push(min_val);
            min_val = x;
        }
        st.push(x);
    }
     
    void pop() {
        int t = st.top(); st.pop();
        if (t == min_val) {
            min_val = st.top(); st.pop();
        }
    }
     
    int top() {
        return st.top();
    }
     
    int getMin() {
        return min_val;
    }
private:
    int min_val;
    stack<int> st;
};

3.2 该题的设计思路及伪代码

利用两个栈，一个栈用于存放入栈元素，另一个用于存放最小元素

伪代码

遍历元素
  if x<最小元素，入存放最小元素栈
   else 入存放元素栈
输出最小元素
##3.3 分析该题目解题优势及难点。
代码简洁，构建函数，函数封装好，代码易懂