终于补完坑了哈哈哈
这个东西很神奇,看了半天网上的解释和课件,研究了很长时间,算是大概明白了它的原理。
话不多说先上图。
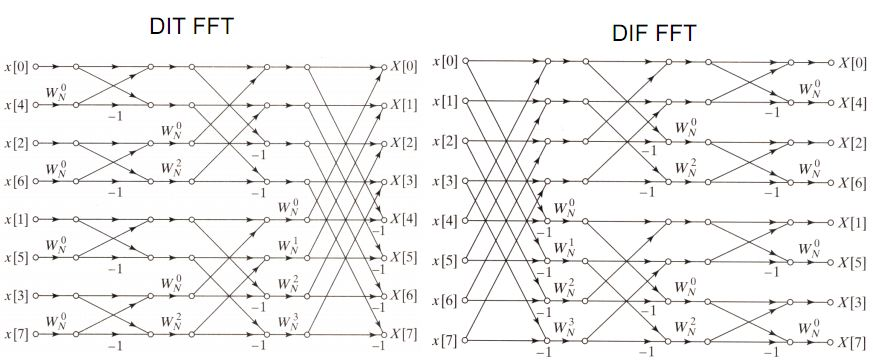
我们要求的h(x)=f(x)*g(x),f(x)=Σai*x^i,g(x)=Σbi*x^i.
朴素求复杂度是$n^2$的,但一个$x$次多项式在平面上可以由$x+1$个点唯一插值表示,所以我们可以先用求出$x+1$个点$(xi,f(xi))$和$(xi,g(xi))$,再求出$(xi,f(xi)*g(xi))$,就可以反解出$h(x)$的表达式。
那么我们需要在$nlogn$的时间内干完这两步,首先xi的取值需要特殊取,令$xi=ζ_{n}^i$(不懂复数的同学可以自行百度),令n(多项式次数,不够的话也要补)=$2^m$,那么
 $(ζ_n^k=ζ_{n/2}^{k/2})$
$(ζ_n^k=ζ_{n/2}^{k/2})$
这显然是一个分治的形式,一个节点可以转移到下一层的两个节点,而每个节点又由上一层的两个节点转移,一共$logn$层,所以复杂度是$nlogn$的。
所以按这个式子分治下去,a0,a2,a4会不停排到前边去,最后的顺序变成图里的0,4,2,6,1,5,3,7,即把它们的二进制补零后翻转然后重新排序(证明很好证,可以自行脑补)。
放代码。
typedef complex<double> E;
for (int i = 1; i < n; i <<= 1)
{
E wn(cos(pi / i), f*sin(pi / i));
for (int j = 0; j < n; j += (i << 1))
{
E w(1, 0);
for (int k = 0; k < i; k++, w *= wn)
{
E x = a[j + k],y=w*a[j+k+i];
a[j + k] = x + y; a[j + k + i] = x - y;
}
}
}第一个循环枚举每回合并的区间长度,然后j每回跳2*i个单位,前i个由x+y转移,后i个由x-y转移,对应图上由左边和左下转移的点和由左边和左上转移的点,至于为什么这么转移。。。。。
第i层第k(从0开始)个节点代表的意义是把ζ(2^i,k%(2^i))带进一个多项式里所得的值,多项式为a0+a1*x+a2*x^2......,其中a数组是排好序的,举个例子:第二列第一个点是
a0+a4(原数组的第四个)*x,第三个点为a2+a6*x,第四个也为a2+a6*x(不过因为x不同所以值不同),第三列第五个为a1+a5*x+a3*x^2+a7*x^3。
又因为ζ(n,k)=-ζ(n,k+n/2),参考分治形式转移就很好解释了。
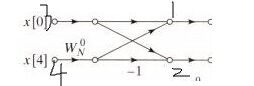
1号点的x=ζ(2,0),二号点为ζ(2,1),
f1=a0+a4*ζ(2,0)=f(3)+f(4)*ζ(2,0),
f2=a0+a4*ζ(2,1)=a0-a4*ζ(2,2)=a0-a4*ζ(2,0)=f(3)-f(4)*ζ(2,0)。
这就可以解释代码中w值相同但一个正一个负了。
(有什么不懂的地方可以留言,我会及时补充的>_<)。
(感谢lty大佬的帮助 )。