一、数据之间的关系
线性关系、一对一、一对多、多对多
二、复杂度
1.时间复杂度:耗费时间的长度
一次for循环的时间复杂度:O(N)
两次for循环嵌套的时间复杂度:O(N2)
计算多个语句混合的时间复杂度,以耗时最久语句的时间复杂度为准。
算法的时间复杂度,用来度量算法的运行时间,记作: T(n) = O(f(n))。它表示随着 输入大小n 的增大,算法执行需要的时间的增长速度可以用 f(n) 来描述。
2.空间复杂度:占用存储单元的长度
3.如果计算时间复杂度、空间复杂度?
三、线性关系
数组、链表、栈、队列都属于线性关系。
四、补充:C语言指针的知识
1.符号*,&,->分别是什么意思?
用做修饰符时,*表示指针,&表示别名
int *p; // p是一个指针
int &a = b; //a是b的别名(必须初始化)
而用作运算符时,*表示取值,&表示取地址
int a = 1;
int *p = &a; //取a的地址并初始化指针p
*p = 2; //修改p指向的值为2(a变成了2)
另外,如果存在m->n , 其含义是 (*m).n
2.typedef 为一种数据类型定义一个新名字。
typedef char* PCHAR; //表示可以用PCHAR表示char*类型
四、链表
1.链表的节点由元素值Element和存放下一节点的指针Next组成,最后一个节点的指针指向Null
链表由头指针开始,头指针中可以不存储值,也可以存储链表长度等数值。
头指针指向头节点,头节点指向下一个节点,一直到尾节点。
2.链表删掉、插入较快。而数组查询比较快。
3.除了单向链表外,还存在双向链表、循环链表

在java中的应用:LinkedList,LinkedHashMap
五、栈
1.栈的特点:"后入先出" Last In First Out
2.push:入栈 pop:出栈 peek:查看栈顶元素
3.栈的顺序存储可以通过数组实现,也可以通过链表实现。
栈可以看成具有一定操作约束的线性表,只能在一端(栈顶)做插入、删除。
如果用链表实现栈,那么栈顶指针Top应该在链表头,不能设在链表尾。
入栈:新增节点,指向之前的头节点(栈顶Top),成为新的Top
出栈:去掉之前的头节点,下一个节点成为新的栈顶Top
如果Top位于链表尾,那么在做链表删除操作时,无法获取链表尾的前一个节点,也就无法将链表尾的前一个节点存储的指针设置为null,这样无法完成删除操作。
java中的相关类: Stack
六、队列
1.队列特点:"先进先出"
2.队列可以通过链表实现,一个节点表示队列头,一个节点表示队列尾。
入列:只需新增节点,之前的队列尾节点指向新增节点。
出列:去掉队列头。
java中的应用:ArrayBlockingQueue
七、哈希表(散列表)
1.哈希表,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
java中的应用:HashMap
八、树
1.树可以通过二叉树实现。左子树为节点的第一个儿子,右子树为节点的下一个兄弟。
2.树的遍历方式有:先序遍历、中序遍历、后序遍历
先序遍历:根节点,左节点,右节点。
中序遍历:左节点,根节点,右节点。
后序遍历:左节点,右节点,根节点。
示例如下:
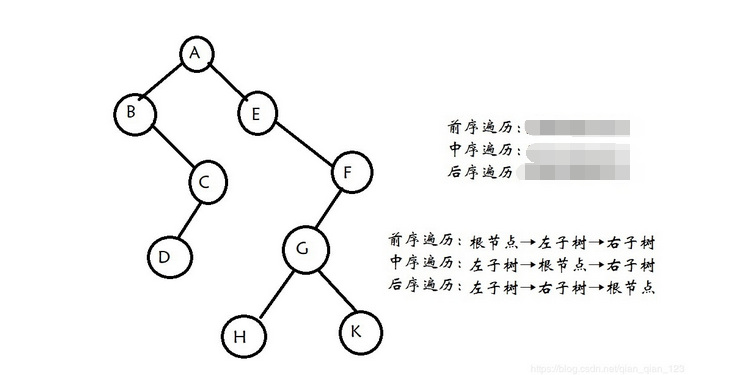
详情参考:https://blog.csdn.net/qian_qian_123/article/details/94491873
3.一棵树当中没有子结点(即度为0)的结点称为叶子结点,简称“叶子”。 叶子是指度为0的结点,又称为终端结点。
九、二叉树
* 二叉查找树:结点值大于左子树,又小于右子树。
二叉查找树(Binary Search Tree),(又名:二叉搜索树,二叉排序树): 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;
* 平衡二叉树,又称AVL树,指的是左子树上的所有节点的值都比根节点的值小,而右子树上的所有节点的值都比根节点的值大,且左子树与右子树的高度差最大为1。因此,平衡二叉树满足所有二叉排序(搜索)树的性质。
其他:红黑树、B树、B+树
* 红黑树,是一种二叉查找树。节点标记为红色或黑色,根节点必须是黑色,规律是“有红必有黑,红红不相连”。
十、图
* 有向图,无向图。
* DFS和BFS,示例图如下:

算法:
1.二分查找法:通过多次分成两半,不断地缩小范围,进行查找
2.分而治之:先将数据"分",然后再抓住交界处进行"治"