Tensorflow 多层全连接神经网络

本节涉及：

1. 身份证问题
2. 单层网络的模型
3. 多层全连接神经网络
4. 激活函数 tanh
5. 身份证问题新模型的代码实现
6. 模型的优化

一、身份证问题

身份证号码是18位的数字【此处暂不考虑字母的情况】，身份证倒数第2个数字代表着性别。

奇数，代表男性，偶数，代表女性

假设事先不知道这个规则，但收集了足够多的身份证及相应的性别信息。希望通过神经网络来找到这个规律

分析：

• 显然，身份证号可以作为神经网络的输入，而持有者的性别即是神经网络计算结果的目标值，所以，我们有完备的训练数据
• 性别有男女，显然是一个二分类问题
• 初步判断，显然不是一个 线性问题 ---->  线性问题一般会随着权重值的变化有一个线性变化的范围
• 分析可得到，这也不是一个 跳变的非线性问题，因为它不像之前的三号学生问题，有一个门槛，门槛内外就是两个分类，所以，原有的单神经元结构可能很难解决这个问题

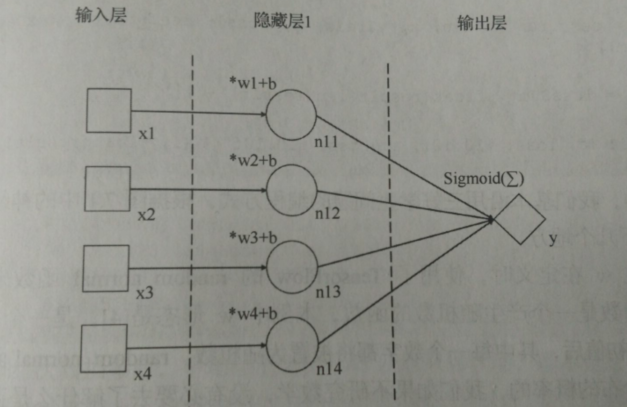
二、单层网络的模型

 

import tensorflow as tf
import random
random.seed()
x = tf.placeholder(tf.float32)
yTrain = tf.placeholder(tf.float32)
w = tf.Variable(tf.random_normal([4], mean=0.5, stddev=0.1), dtype=tf.float32) 
# random_normal 函数是一个产生随机数的函数，此处w 的形态是[4] ，即一个四维的向量，使用此函数赋值后，w其中的每一个数字都会被赋值位随机数
# random_normal 产生的随机数是符合 正态分布概率的，即 随机数会在某个平均值附近的一定范围内波动
# mean 是指定这个平均值的， stddev 是指定这个波动范围的

b = tf.Variable(0, dtype=tf.float32) # 增加了一个 偏移量b,这里是一个标量。也可以定义为和可变参数 w 形态相同的 向量或矩阵

n1 = w * x + b
y = tf.nn.sigmoid(tf.reduce_sum(n1))   # 求和 + sigmoid 函数
loss = tf.abs(y - yTrain)  
optimizer = tf.train.RMSPropOptimizer(0.01)
train = optimizer.minimize(loss)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
lossSum = 0.0

for i in range(10):
    xDataRandom = [int(random.random() * 10), int(random.random() * 10), int(random.random() * 10), int(random.random() * 10)] # 生成随机训练数据
    if xDataRandom[2] % 2 == 0:
        yTrainDataRandom = 0
    else:
        yTrainDataRandom = 1  # 根据生成的随机训练数据的第3项数字得到标准输出数据
    result = sess.run([train, x, yTrain, y, loss], feed_dict={x: xDataRandom, yTrain: yTrainDataRandom})
    lossSum = lossSum + float(result[len(result) - 1])# 记录训练中误差的总和，并且在每次训练时，将它的值除以 训练次数得到平均误差输出，作为参考
    print("i: %d, loss: %10.10f, avgLoss: %10.10f" % (i, float(result[len(result) - 1]), lossSum / (i + 1)))
    #可变参数 w b 的取值在本题中 意义不大，仅观察误差的变化情况就可以了，所以此处输出  本次训练误差 + 累计平均误差

i: 0, loss: 0.9999923706, avgLoss: 0.9999923706
i: 1, loss: 1.0000000000, avgLoss: 0.9999961853
i: 2, loss: 0.1363981962, avgLoss: 0.7121301889
i: 3, loss: 0.9999995232, avgLoss: 0.7840975225
i: 4, loss: 0.9998092055, avgLoss: 0.8272398591
i: 5, loss: 0.0000855923, avgLoss: 0.6893808146
i: 6, loss: 0.9999967813, avgLoss: 0.7337545242
i: 7, loss: 0.0000003576, avgLoss: 0.6420352533
i: 8, loss: 0.9997699857, avgLoss: 0.6817835569
i: 9, loss: 0.9982397556, avgLoss: 0.7134291768

 平均误差有一定的变化，说明神经网络的调节在发挥作用，加大训练次数为5000：

i: 4991, loss: 0.9999963045, avgLoss: 0.4365434793
i: 4992, loss: 1.0000000000, avgLoss: 0.4366563286
i: 4993, loss: 0.0255949926, avgLoss: 0.4365740175
i: 4994, loss: 1.0000000000, avgLoss: 0.4366868155
i: 4995, loss: 0.0000000000, avgLoss: 0.4365994082
i: 4996, loss: 1.0000000000, avgLoss: 0.4367121560
i: 4997, loss: 1.0000000000, avgLoss: 0.4368248587
i: 4998, loss: 0.0178810358, avgLoss: 0.4367410531
i: 4999, loss: 0.0090432763, avgLoss: 0.4366555136

平均误差在 0.43 左右浮动，基本稳定下来，再多加训练次数也不会让误差减小，说明，目前的神经网络模型无法解决这个问题，需要优化

常见的优化神经网络结构的方法包括：

增加神经元节点数量      增加隐藏层的数量

另外本模型中的隐藏层并不是全连接层，全连接层应该是 前后两层的所有节点之间都有连线，我们的结构显然不是，这也是可以优化的

三、多层全连接神经网络

神经网络中，最常见的形式就是 全连接层 -----  各个节点与上一层的每个节点都有连线

深度学习神经网络中，一般都有多个隐藏层顺序排列组成完整的神经网络

（1）矩阵乘法

向量点乘：

两个形态相同的向量相乘，得到的结果是一个形态与他们都相同的新向量，其中的每一个位置的数值都是参与相乘的两个向量相同位置的数值相乘的结果

[1,2,3] * [2,3,4] = [2,6,12]

矩阵的点乘也是类似的，得到的还是相同形态的矩阵，在tensorflow 中，用 “ * ” 表示 点乘

用点乘的形式做出来的神经网络模型就是类似之前的模型结构，输入层各个节点与隐藏层的各个节点之间是有一对一的连线，一对一的连线就代表了 点乘的关系【即向量中相同位置的项才能进行运算】

但遇上的问题，很难用 一对一 的关系 来限定，往往是 事物之间互项有联系且联系关系强弱未知。因此，我们往往 在隐藏层中 设置较多的全连接结构的节点，来覆盖尽可能多的可能性。如果某两节点直接没关系，经过运算会发现 w =0， 说明这条连线其实没有意义

要实现全连接的关系，就要用到 矩阵的乘法：

 

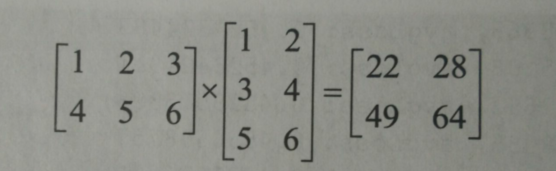
import numpy as np
a = [[1,2,3],[4,5,6]]
b = [[1,2],[3,4],[5,6]]
c = np.matmul(a,b)
print(c)

[[22 28]
 [49 64]]

numpy 包中的 matmul() 函数就是用来进行矩阵乘法运算的

由上方示例可知：

1. 当且仅当 前面矩阵的列数等于等于后面矩阵的行数时，二矩阵才可以进行矩阵乘法【叉乘】
2. 新矩阵的行数 等于前面矩阵的行数，新矩阵的列数 等于后面矩阵的列数
3. 矩阵的乘法是有顺序的

 另外，结果矩阵中，每个数值都是 点乘求和的结果，也就是说明这个值与参与计算的对应矩阵的对应行列的数值都是有关系的，把整个结果矩阵的所有数值合起来看，里面有参与计算的两个矩阵中的所有数值的贡献，因此，我们可以把这看作一种”全连接关系“。 ————>   即，可以用矩阵的乘法实现”全连接“关系

（2）用矩阵乘法实现全连接层

 用之前三好学生的例子来做用矩阵乘法实现全连接关系的详细说明

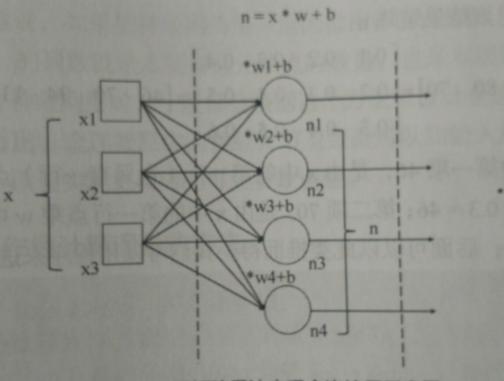
相关解释：

1. 输入层仍然使用 x 表示，有3个项，分别代表德 智 体 三个得分
2. 隐藏层有4个节点，用张量n 表示，且输入层与隐藏层的各个节点是全连接的

用矩阵乘法实现这个全连接关系：

（A）确定参与运算的都是矩阵

x 是一个向量，并非矩阵【因为向量在计算机中的表达形式是 一维数组，而矩阵是二维数组】

所以，需要把x 转化为 矩阵

x = [90,80,70]

可以把x 转换为 1 * 3 矩阵 ，即形态为 [1,3] 的二维数组

x = [[90,80,70]]

二维数组 x ,第一个维度只有一项，对于矩阵来说就是一行

第二个维度是3项分数，对于矩阵来说就是3列

在隐藏层中，我们准备用 4 个神经元节点来处理，意味着 隐藏层对下一层输出的数据项会是4个，用矩阵表达，就是需要隐藏层的输出结果是一个 1X 4 矩阵，也就是一个形态为 [1,4] 的二维数组

所以，隐藏层中的可变参数 w 现在也需要是 矩阵的形式。由 新矩阵的行数 等于前面矩阵的行数，新矩阵的列数 等于后面矩阵的列数 可知：

二矩阵相乘后的结果矩阵：

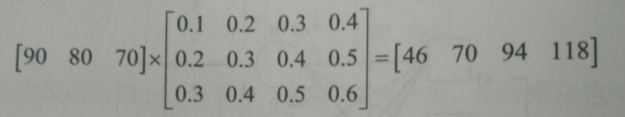
 所以，w 需要是一个 3 X 4 的矩阵

（B）体现全连接关系

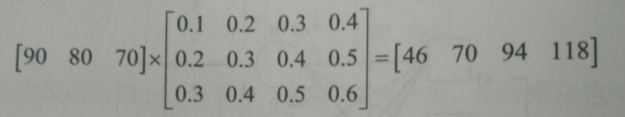
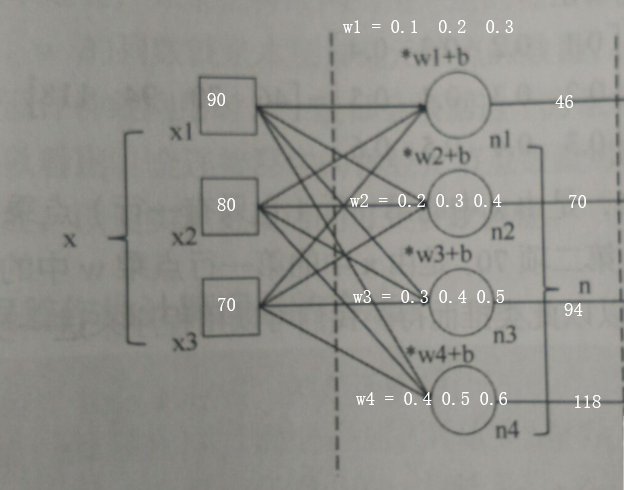
 第一个节点的输出 46 = 90 * 0. 1 + 80 * 0.2 + 70 * 0.3 = 9 + 16 + 21 = 46。其余节点同理

设计思想：

对于输入形态[1,3] 的矩阵x ，将其每一项 看作是 输入层的一个节点，对于隐藏层的节点n ，把它每一项也看做 一个节点，也就是 46 70 94 118 对应的节点n1 n2 n3 n4

对于可变参数w，我们把它的每一列组成一个向量，w1 w2 w3 w4

可以由矩阵的运算规律，隐藏层中的第一个节点 n1 的计算过程是 x1 x2 x3 组成的向量 与 向量w1  点乘求和后得到，即节点n1 的输出结果中包含了所有输入节点的贡献，即 n1 是与输入层所有节点都是有关系的，n2 n3 n4也同理。反过来看，对于每个输入层的节点 ，都与每个隐藏层的节点都有关系，这样的 两层之间不同节点都有连接关系的层，就是全连接层。

由上，用矩阵乘法可以很方便的实现全连接关系

总结：

如果把神经网络的每一层的输出 都看成矩阵，矩阵w 的行数要等于上一层的输出矩阵的列数，w的列数就是本层神经元节点的数量，也是本层输出矩阵的列数

 

一般会让全连接层的节点多于输入层的节点数，以便实现更灵活的可变参数调整

（3）使用均方误差作为计算误差的方法

 我们之前计算误差的时候，都是

loss = tf.abs(y - yTrain)

y 是神经网络的计算结果，yTrain 是目标值，abs 是 tensorFlow 中取绝对值的函数

这种方式更适合数值范围较大的情况

而三好学生的评选结果 身份证问题 都是一个 二分类问题中的概率： 比如，“1” 是三号学生的概率为 100% ，“0” 是三好学生的概率是 0% , "0.2" 是三好学生的概率是 20%

对于结果是分类概率的问题，均方误差是一种更好的误差计算方法

均方误差：是指结果值向量中各数据项偏离目标值的距离的平方和的平均数，也就是误差平方和的平均数

 代码验证：

import tensorflow as tf
y = tf.placeholder(dtype=tf.float32)
yTrain = tf.placeholder(dtype=tf.float32)
loss = tf.reduce_mean(tf.square(y-yTrain))

sess = tf.Session()

print(sess.run(loss,feed_dict={y:[0.2,0.8],yTrain:[1,0]}))
print(sess.run(loss,feed_dict={y:[0.2,0.8],yTrain:[0,1]}))
print(sess.run(loss,feed_dict={y:[1.0,0.0],yTrain:[0,1]}))
print(sess.run(loss,feed_dict={y:[1.0,0.0],yTrain:[1,0]}))
print(sess.run(loss,feed_dict={y:[0.2,0.3,0.5],yTrain:[1,0,0]}))
print(sess.run(loss,feed_dict={y:[0.2,0.3,0.5],yTrain:[0,1,0]}))
print(sess.run(loss,feed_dict={y:[0.2,0.3,0.5],yTrain:[0,0,1]}))

0.64000005
0.04
1.0
0.0
0.32666668
0.26
0.12666667

解释：

上方代码中，为了直接看到均方误差的计算结果，把y 也定义成一个占位符，以便后续直接喂数据

tf.square 求平方值的函数，可以对标量求平方，也可以对向量求平方【每一项平方】

tf.reduce_mean 是对一个矩阵（或向量） 中的所有数求平均值

loss = tf.reduce_mean(tf.square(y-yTrain))  就是求y 与 yTrain 的均方差

最后几条，尝试用均方误差计算三分类问题的误差

四、激活函数 tanh

之前，我们使用的是 sigmoid函数 进行神经网络的去线性化，把任意一个数字收敛到 [0，1] 的范围内，从而把一组线性的数据 转换为 非线性的数据

tanh 也是一个去线性化的函数，会把任何一个数字转换为 [-1,1] 范围内的数字

 在设计神经网络的隐藏层时，根据实际情况 选择 哪种激活函数（一般一层只使用一种激活函数）

五、身份证问题新模型及代码实现

将本题的模型改成多层全连接神经网络：

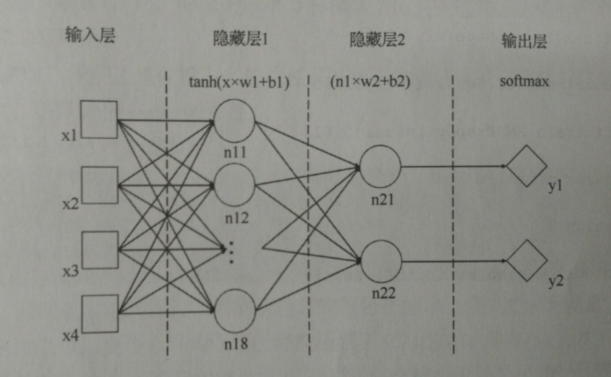
 对图7.4中的模型做简单说明:这是一个由一 个输入层、 两个隐藏层和一个输出层组成的多层全连接神经网络模型，其中两个隐藏层都是全连接层。输入层有4个节点;隐藏层 1 有8个节点，分别表示为 n11~n18;隐藏层 2有两个节点，分别表示为n21和n22。隐藏层1使用了激活函数tanh,隐藏层2没有使用激活函数;隐藏层1的计算操作是nl = tanh(x * wI+b1 ),其中nl为图7.4中的n11~n18这些节点组成的向量，wI和 bl分别为本层节点的权重和偏移量，乘法符号 " * " 是表示又乘:隐藏层2的计算操作是n2 = tanh(n2 * w2+b2 ),其中 m2为图7.4中的n21和n22组成的向量，w2 和b2分别为本层节点的权重和偏移量，n2与w2间的乘法也是又乘。输出层有两个节点。是对隐藏层2的输出应用了softmax函数来进行二分类的结果。

代码实现：

import tensorflow as tf
import random
random.seed()
x = tf.placeholder(tf.float32)
yTrain = tf.placeholder(tf.float32)
w1 = tf.Variable(tf.random_normal([4, 8], mean=0.5, stddev=0.1), dtype=tf.float32)
# 可变参数 w1 形态为[ 4,8 ] 是为了保证输出到下一层的结点数是8，同样w2 的形态是 [ 8,2 ] ，是为了保证 输出到 输出层的节点数 为 2
# 以便用 softmax 函数二分类 
# 其中的  [x , y] 可理解为 “承前启后” ，x = 前面的神经元节点 ， y = 后面的神经元节点
# 具体含义，往上翻，见“矩阵乘法”

b1 = tf.Variable(0, dtype=tf.float32)
# b1 b2 都被定义为标量，标量在于向量或举证进行加法等操作时，会对向量或矩阵中的每一个元素都执行相同的操作。也可以把偏移量设置成向量
xr = tf.reshape(x, [1, 4])
# 把输入数据x 从一个4维向量 准换为一个形态为 [1,4] 的矩阵，并保存至向量 xr 中
n1 = tf.nn.tanh(tf.matmul(xr, w1)  + b1)
# 定义隐藏层 1 的结构，tf.matmul 函数为 tensorFlow 中进行矩阵乘法的函数，tf.nn.tanh 为激活函数 tanh

w2 = tf.Variable(tf.random_normal([8, 2], mean=0.5, stddev=0.1), dtype=tf.float32)
b2 = tf.Variable(0, dtype=tf.float32)
n2 = tf.matmul(n1, w2) + b2
y = tf.nn.softmax(tf.reshape(n2, [2]))
# 是输出层对隐藏层 2 的输出 n2 进行 softmax 函数处理，使得结果是一个相加为 1 的向量
# 由于 n2 的形态 [1,2] 是一个矩阵，所以先把它转化为 一个形态为 [2] 的一维向量【一维数组】
loss = tf.reduce_mean(tf.square(y - yTrain))
# 误差计算 采用了 均方误差
optimizer = tf.train.RMSPropOptimizer(0.01)
train = optimizer.minimize(loss)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
lossSum = 0.0

for i in range(5):
    xDataRandom = [int(random.random() * 10), int(random.random() * 10), int(random.random() * 10), int(random.random() * 10)]
    if xDataRandom[2] % 2 == 0:
        yTrainDataRandom = [0, 1]
    else:
        yTrainDataRandom = [1, 0]
    # 由于采用了 均方误差的计算方法，需要将目标值 由 1 变为 [1,0] ，由 0 变为 [0,1],这样，喂给目标值 yTrian 的才是需要的 二维向量
    result = sess.run([train, x, yTrain, y, loss], feed_dict={x: xDataRandom, yTrain: yTrainDataRandom})
    lossSum = lossSum + float(result[len(result) - 1])
    print("i: %d, loss: %10.10f, avgLoss: %10.10f" % (i, float(result[len(result) - 1]), lossSum / (i + 1)))
    # 输出训练误差 + 平均误差

i: 0, loss: 0.2222173959, avgLoss: 0.2222173959
i: 1, loss: 0.2899080217, avgLoss: 0.2560627088
i: 2, loss: 0.2773851454, avgLoss: 0.2631701877
i: 3, loss: 0.2356697619, avgLoss: 0.2562950812
i: 4, loss: 0.2243882120, avgLoss: 0.2499137074

可以看到，平均误差趋势在减小，增大训练次数为50000：

i: 49992, loss: 0.1980789304, avgLoss: 0.1934479160
i: 49993, loss: 0.0004733017, avgLoss: 0.1934440560
i: 49994, loss: 0.3544868231, avgLoss: 0.1934472772
i: 49995, loss: 0.2939709425, avgLoss: 0.1934492878
i: 49996, loss: 0.0005629645, avgLoss: 0.1934454299
i: 49997, loss: 0.0000229554, avgLoss: 0.1934415612
i: 49998, loss: 0.0003532485, avgLoss: 0.1934376994
i: 49999, loss: 0.2427534610, avgLoss: 0.1934386857

 多次训练后，还是未能达到一个非常小的误差，说明这一类非线性跳动问题解决起来比较复杂

六、模型的优化

●增加隐藏层的神经元节点数量。这是最容易实施的方法了，例如要把图7.4模型中，隐藏层1的节点数增加到32个，只需要把wl定义成形态为[14, 32]的变量，同时把w2定义为形态为[32, 2]的变量。修改后，循环50万次后，误差大约已经能够减小到0.09左右。我们要注意，由于神经网络调节可变参数的初值一般是随机数，另外优化器对可变参数的调节也有定随机性， 所以每次程序执行训练后的结果有所不同是正常的，但大体趋势应该近似。也不排除优化器落入“陷阱”， 导致误差始终无法收敛的情况，这时候重新进行训练，从另组可变参 数随机初始值开始即可。

●增加隐藏层的层数。 一般来说， 增加某个隐藏层中神经元节点的数量，可以形象地理解成让这层变“胖”;那么，增加隐藏层的层数就是让神经网络变“高”或者变“长”;一般来说， 增加层数比增加神经元的数量会效果好点，但是每一层上激话函数的选择需要动些胸筋，有些层之间激活函数的组合会遇上意料不到的问题。层数太多时，有时候还会造成优化器感知不畅而无法调节可变参数。另外，只增加线性全连接层的数量一般是没有意义的， 因为两个线性全连接层是可以转换成一层的。这些留到进阶学习的时候去提高。

下面给出段代码， 是在代码7.2的基础上加入一个隐藏层n3. 大家可以看看如何增加新的隐藏层，同时回顾矩阵乘法的有关知识。

import tensorflow as tf
import random
random.seed()
x = tf.placeholder(tf.float32)
yTrain = tf.placeholder(tf.float32)
w1 = tf.Variable(tf.random_normal([4, 32], mean=0.5, stddev=0.1), dtype=tf.float32)
b1 = tf.Variable(0, dtype=tf.float32)
xr = tf.reshape(x, [1, 4])
n1 = tf.nn.tanh(tf.matmul(xr, w1)  + b1)
w2 = tf.Variable(tf.random_normal([32, 32], mean=0.5, stddev=0.1), dtype=tf.float32)
b2 = tf.Variable(0, dtype=tf.float32)
n2 = tf.nn.sigmoid(tf.matmul(n1, w2) + b2)
w3 = tf.Variable(tf.random_normal([32, 2], mean=0.5, stddev=0.1), dtype=tf.float32)
b3 = tf.Variable(0, dtype=tf.float32)
n3 = tf.matmul(n2, w3) + b3
y = tf.nn.softmax(tf.reshape(n3, [2]))
loss = tf.reduce_mean(tf.square(y - yTrain))
optimizer = tf.train.RMSPropOptimizer(0.01)
train = optimizer.minimize(loss)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
lossSum = 0.0
for i in range(5000):
    xDataRandom = [int(random.random() * 10), int(random.random() * 10), int(random.random() * 10), int(random.random() * 10)]
    if xDataRandom[2] % 2 == 0:
        yTrainDataRandom = [0, 1]
    else:
        yTrainDataRandom = [1, 0]
    result = sess.run([train, x, yTrain, y, loss], feed_dict={x: xDataRandom, yTrain: yTrainDataRandom})
    lossSum = lossSum + float(result[len(result) - 1])
    print("i: %d, loss: %10.10f, avgLoss: %10.10f" % (i, float(result[len(result) - 1]), lossSum / (i + 1)))

●适当调节学习率。有时候，学习率不合适也会导致训练效率不高，可以适当修改。具体见以后