涉及:
- 使用交叉验证对模型进行评估
- 使用网格搜索寻找模型的最优参数
- 对分类模型的可信度进行评估
使用交叉验证进行模型评估
以前的内容,经常涉及使用sklear中的train_test_split 将数据集拆分成训练集和测试集,然后用训练集训练模型,再用模型去拟合测试集并对模型进行评分,来评估模型的准确度
1.sklearn中的交叉验证法
统计学中,交叉验证是一种常用于对于模型泛化性能进行评估的方法
和train_test_split方法不同的是,交叉验证会反复地拆分数据集,并用来训练多个模型
sklearn中默认使用的是 K折叠交叉验证法:

还有“随机拆分交叉验证法”,“挨个儿试法”
交叉验证的使用方法:
#导入红酒数据集 from sklearn.datasets import load_wine #导入交叉验证工具 from sklearn.model_selection import cross_val_score #导入用于分类的支持向量机模型 from sklearn.svm import SVC #载入红酒数据集 wine = load_wine() #设置SVC的核函数为linear svc = SVC(kernel='linear') #使用交叉验证法对SVC进行评分 scores = cross_val_score(svc,wine.data,wine.target) #得分 print(scores)
[0.83333333 0.95 1. ]
【结果分析】
先导入了scikit_learn的交叉验证评分类,然后使用SVC对酒的数据集进行分类,默认情况下,cross_val_score会使用3个折叠,因此,会得到3个分数
模型的得分:
#使用.mean() 获得分数的平均值 print(scores.mean())
0.9277777777777777
【结果分析】
交叉验证法平均分为0.928分
将数据集拆成6个部分来评分——cross_val_score:
#设置cv参数为6 scores = cross_val_score(svc,wine.data,wine.target,cv=6) print(scores)
[0.86666667 0.9 0.93333333 0.96666667 1. 1. ]
print(scores.mean())
0.9444444444444445
【结果分析】
在sklearn中,cross_val_score对于分类模型默认使用的是K折叠交叉验证,而对于分类模型则默认使用分层K交叉验证法
要解释啥是分层K交叉验证法,先分析下酒的数据集:
#打印红酒数据集的分类标签 print(wine.target)


2.随机拆分和“挨个儿试”
随机拆分原理——先从数据集中随机抽一部分数据作为训练集,再从其余的部分随机抽一部分作为测试集,进行评分后再迭代,重复上一步操作,直到把我们希望的迭代次数全跑完
#导入随机拆分工具 from sklearn.model_selection import ShuffleSplit #设置拆分的数为10个 shuffle_split = ShuffleSplit(test_size=.2,train_size=.7,n_splits=10) #对拆分好的数据进行交叉验证 scores = cross_val_score(svc,wine.data,wine.target,cv=shuffle_split) print(scores)
把每次迭代的测试集设为数据集的20%,而训练集为70%,并且把整个数据集拆分成10个子集

【结果分析】
ShuffleSplit一共为SVC模型进行了10次评分,最终得分即10个评分的平均值
挨个儿试试:
把每个数据点都当成一个数据集,所以数据集里有多少样本,它就迭代多少次
数据集较大——很耗时
数据集较小——评分准确度最高
#导入LeaveOneOut from sklearn.model_selection import LeaveOneOut #设置cv参数为leaveoneout cv = LeaveOneOut() #重新进行交叉验证 scores = cross_val_score(svc,wine.data,wine.target,cv=cv) print('迭代次数:',len(scores)) print('平均分:',scores.mean())
迭代次数: 178 平均分: 0.9550561797752809
【结果分析】
由于酒的数据集中有178个样本,所以迭代了178次
为啥要用交叉验证法?

使用网格搜索优化模型参数
1.简单网格搜索
用lasso算法为例:
在Lasso算法中,有两个参数比较重要——正则化参数alpha,最大迭代次数max_iter
默认情况下alpha=1.0,max_iter=1000
假设,想试试当alpha分别取10.0 1.0 0.1 0.01这4个数值,而max_iter 分别取 100 1000 5000 10000时,模型表现有什么差别
如果按照手动调整的话,试16次。。。
#导入套索回归模型 from sklearn.linear_model import Lasso #导入数据集拆分工具 from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(wine.data,wine.target,random_state = 38) #设置初始分数为0 best_score = 0 #设置alpha的参数遍历0.01,0.1,1,10 for alpha in [0.01,0.1,1,10]: #最大迭代数遍历100,1000,5000,10000 for max_iter in [100,1000,5000,10000]: lasso = Lasso(alpha=alpha,max_iter=max_iter) #训练套索回归模型 lasso.fit(X_train,y_train) score = lasso.score(X_test,y_test) #令最佳分数为所有分数中的最高值 if score >best_score: best_score = score #定义字典,返回最佳参数和最佳迭代数 best_parameters={'alpha':alpha,'最大迭代数':max_iter} print('最高分:',best_score) print('最佳参数设置',best_parameters)
最高分: 0.8885499702025688
最佳参数设置 {'alpha': 0.01, '最大迭代数': 100}
【结果分析】
快速找到了~~
局限性:
所进行的16次评分都是基于同一个训练集和测试集,这只能代表模型在该训练集和测试集的得分情况,不能反映出新的数据集的情况
举例:
修改train_test_split的random_state参数:【38--> 0】
#导入套索回归模型 from sklearn.linear_model import Lasso #导入数据集拆分工具 from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(wine.data,wine.target,random_state = 0) #设置初始分数为0 best_score = 0 #设置alpha的参数遍历0.01,0.1,1,10 for alpha in [0.01,0.1,1,10]: #最大迭代数遍历100,1000,5000,10000 for max_iter in [100,1000,5000,10000]: lasso = Lasso(alpha=alpha,max_iter=max_iter) #训练套索回归模型 lasso.fit(X_train,y_train) score = lasso.score(X_test,y_test) #令最佳分数为所有分数中的最高值 if score >best_score: best_score = score #定义字典,返回最佳参数和最佳迭代数 best_parameters={'alpha':alpha,'最大迭代数':max_iter} print('最高分:',best_score) print('最佳参数设置',best_parameters)
最高分: 0.8298747376836272
最佳参数设置 {'alpha': 0.1, '最大迭代数': 100}
【结果分析】
稍微对train_test_split拆分数据集的方式做一点变更,最高分酒降到了0.83
最佳alpha参数为0.1
为了解决这个问题——与交叉验证结合的网格搜索
2.与交叉验证结合的网格搜索
#导入numpy import numpy as np #设置alpha的参数遍历0.01,0.1,1,10 for alpha in [0.01,0.1,1.0,10.0]: #最大迭代数遍历100,1000,5000,10000 for max_iter in [100,1000,5000,10000]: lasso = Lasso(alpha=alpha,max_iter=max_iter) scores = cross_val_score(lasso,X_train,y_train,cv=6) score = np.mean(scores) #令最佳分数为所有分数中的最高值 if score >best_score: best_score = score #定义字典,返回最佳参数和最佳迭代数 best_parameters={'alpha':alpha,'最大迭代数':max_iter} print('最高分:',best_score) print('最佳参数设置',best_parameters)
最高分: 0.8652073211223437
最佳参数设置 {'alpha': 0.01, '最大迭代数': 100}
【结果分析】
这里我们做了一点手脚,就是只用先前拆分好的X_train来进行交叉验证,以便于我们找到最佳参数后,再用来拟合X_test 来看一下模型的得分
#用最佳参数模型拟合数据 lasso = Lasso(alpha=0.01,max_iter=100).fit(X_train,y_train) print('数据集得分:',lasso.score(X_test,y_test))
数据集得分: 0.819334891919453
【结果分析】
此处,并不是参数的问题,而是lasso算法会对样本的特征进行正则化,导致一些特征的系数变为0,也就是说会抛弃一些特征值
对于酒集来说,本身特征就不多,因此使用lasso进行分类,得分会相对低些
在sklearn中,内置了一个类,GridSearchCV,进行参数调优的过程简单:
#导入网格搜索工具 from sklearn.model_selection import GridSearchCV #将需要遍历的参数定义为字典 params = {'alpha':[0.01,0.1,1.0,10.0],'max_iter':[100,1000,5000,10000]} #定义网格搜索中使用的模型和参数 grid_search = GridSearchCV(lasso,params,cv=6) #使用网格搜索模型拟合数据 grid_search.fit(X_train,y_train) print('模型最高分:',grid_search.score(X_test,y_test)) print('最优参数:',grid_search.best_params_)
模型最高分: 0.819334891919453
最优参数: {'alpha': 0.01, 'max_iter': 100}
【结果分析】
GridSearchCV中的best_scores_ 属性,会存储模型在交叉验证中所得的最高分,而不是测试集上的得分
#打印网格搜索中的best_score_属性 print('交叉验证最高分:',grid_search.best_score_)
交叉验证最高分: 0.8653192931146032
【结果分析】
这里的得分和cross_val_score得分是完全一致的,说明GridSearchCV 本身就是将交叉验证和网格搜索封装一起的方法
GridSearchCV虽然强悍,但需要反复建模——> 所需要的计算时间往往更长
分类模型的可信度评估
实际上算法在分类过程中,会认为某个数据点80%可能性属于分类1,20%可能性属于分类0,模型会依据“可能性较大”的方式分配分类标签
算法是如何对这种分类的可能性进行计算的?
1.分类模型中的预测准确率
在sklearn中,很多用于分类的模型都有一个 predict_proba功能——用于计算模型在对数据集进行分类时,每个样本属于不同分类的可能性是多少
#导入数据集生成工具 from sklearn.datasets import make_blobs #导入画图工具 import matplotlib.pyplot as plt #生成样本数为200,分类为2,标准差为5的数据集 X,y = make_blobs(n_samples=200,random_state=1,centers=2,cluster_std =5) #绘制散点图 plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.cool,edgecolor='k') plt.show()
使用make_blobs 制作数据集,为了给算法点难度,故意把数据集的方差设高点cluster_std=5
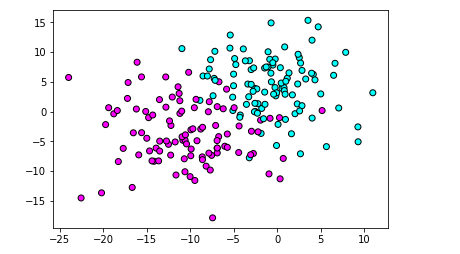
【结果分析】
像评价女朋友衣服——红色--好看,青蓝色—不好看,中间的点—还可以
使用高斯朴素贝叶斯分类:
#导入高斯贝叶斯模型 from sklearn.naive_bayes import GaussianNB X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=68) #训练高斯贝叶斯模型 gnb = GaussianNB() gnb.fit(X_train,y_train) #获得高斯贝叶斯的分类准确概率 predict_proba = gnb.predict_proba(X_test) print('预测准确率形态:',predict_proba.shape)
预测准确率形态: (50, 2)
【结果分析】
在predict_proba 属性中存储了50个数组【即测试集大小】,每个数组有2个元素
打印一下前5个:
#打印准确概率的前5个 print(predict_proba[:5])
[[0.98849996 0.01150004] [0.0495985 0.9504015 ] [0.01648034 0.98351966] [0.8168274 0.1831726 ] [0.00282471 0.99717529]]
【结果分析】
反应的是测试集前5个样本的分类准确率
用图像直观看下predict_proba 在分类过程中的表现:
#设定横纵轴范围 x_min,x_max= X[:,0].min()-.5,X[:,0].max()+.5 y_min,y_max= X[:,1].min()-.5,X[:,1].max()+.5 xx,yy = np.meshgrid(np.arange(x_min,x_max,0.2),np.arange(y_min,y_max,0.2)) Z = gnb.predict_proba(np.c_[xx.ravel(),yy.ravel()])[:,1] Z = Z.reshape(xx.shape) #绘制等高线 plt.contourf(xx,yy,Z,cmap=plt.cm.summer,alpha=.8) #绘制散点图 plt.scatter(X_train[:,0],X_train[:,1],c=y_train,cmap=plt.cm.cool,edgecolor='k') plt.scatter(X_test[:,0],X_test[:,1],c=y_test,cmap=plt.cm.cool,edgecolor='k',alpha=0.6) #设置横纵轴范围 plt.xlim(xx.min(),xx.max()) plt.ylim(yy.min(),yy.max()) #设置横纵轴的单位 plt.xticks(()) plt.yticks(()) plt.show()
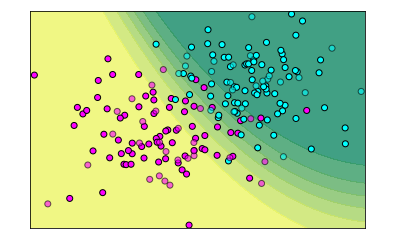
【结果分析】
圆点代表样本数据
棕色为第一个分类,蓝色为第二个分类,渐变色区域,就是模型觉得“还可以”的部分

2.分类模型中的决定系数
同预测准确率类似,决定系数decision_function 也会给我们返回一些数值——告诉我们模型认为某个数据点处于某个分类的“把握”有多大
不同的是,在二元分类任务中,只返回一个值——正数,属于分类1;负数,属于分类2
高斯朴素贝叶斯没有decision_function属性——> 使用支持向量机SVM算法建模:
#导入SVC模型 from sklearn.svm import SVC #使用训练集训练模型 svc = SVC().fit(X_train,y_train) #获得SVC的决定系数 dec_func = svc.decision_function(X_test) #打印决定系数中的前5个 print(dec_func[:5])
[ 0.02082432 0.87852242 1.01696254 -0.30356558 0.95924836]
图形化展示desicion_function原理:
#使用决定系数绘图 Z = svc.decision_function(np.c_[xx.ravel(),yy.ravel()]) Z = Z.reshape(xx.shape) #绘制等高线 plt.contourf(xx,yy,Z,cmap=plt.cm.summer,alpha=.8) plt.scatter(X_train[:,0],X_train[:,1],c=y_train,cmap=plt.cm.cool,edgecolor='k') #绘制散点图 plt.scatter(X_test[:,0],X_test[:,1],c=y_test,cmap=plt.cm.cool,edgecolor='k',alpha=0.6) plt.title('SVC decision_function') #设置横纵轴范围 plt.xlim(xx.min(),xx.max()) plt.ylim(yy.min(),yy.max()) #设置横纵轴的单位 plt.xticks(()) plt.yticks(()) plt.show()


.score给模型评分的方法
- 对于分类模型来说,默认情况下,.score给出的是模型分类的准确率
- 对于回归模型来说,默认情况下, .score给出的是回归分析中的R2分数【即,可决系数或拟合优度】
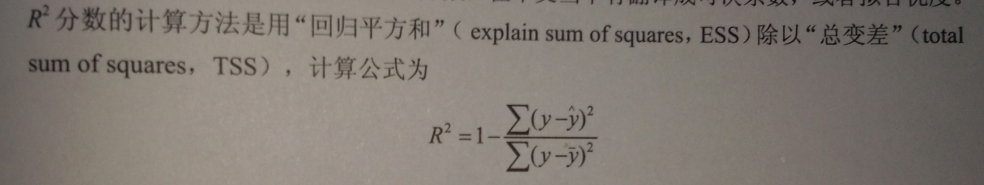
其他评分的方法:

GridSearchCV改变评分的方式:

#修改scoring参数为roc_auc grid = GridSearchCV(RandomForestClassifier*(,param_grid = param_grid,scoring = 'roc_auc')
这样,模型的参数就是 roc_auc 方式了