引子
《数学之美》介绍布隆过滤器非常经典:
在日常生活中,包括设计计算机软件时,经常要判断一个元素是否在一个集合中。比如:
- 在字处理软件中,需要检查一个英语单词是否拼写正确(也就是要判断它是否在已知的字典中);
- 在FBI,一个嫌疑人的名字是否已经在嫌疑犯的名单上;
- 在网络爬虫里,一个网站是否已访问过;
- yahoo, gmail等邮箱垃圾邮件过滤功能,等等 ...
以上场景需要解决的共同问题是:如何查看一件事物是否在有大量数据的集合里。
通常的做法有以下几种思路:
- 数组、
- 链表、
- 树、平衡二叉树、Trie
- map (红黑树)
- 哈希表
上面这几种数据结构配合一些搜索算法是可以解决数据量不大的问题,但当集合里面的数据量非常大的时候,就会出现问题。比如:有500万条记录甚至1亿条记录?这个时候常规的数据结构的问题就凸显出来了。数组、链表、树等数据结构会存储元素的内容,一旦数据量过大,消耗的内存也会呈现线性增长,最终达到瓶颈。哈希表查询效率可以达到O(1)。但是哈希表需要消耗的内存依然很高。使用哈希表存储一亿 个垃圾 email 地址的消耗?哈希表的做法:首先,哈希函数将一个email地址映射成8字节信息指纹;考虑到哈希表存储效率通常小于50%(哈希冲突);因此消耗的内存:8 * 2 * 1亿 字节 = 1.6GB 内存。因此,存储几十亿个邮件地址就可能需要上百GB的内存。除非是超级计算机,一般服务器是无法存储的。这个时候,布隆过滤器(Bloom Filter)就应运而生。
布隆过滤器
Bloom Filter是由伯顿 · 布隆(Burton Bloom)于1970年提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。我们由上面的例子来说明其工作原理。
假定存储一亿个电子邮件地址,先建立一个16亿二进制(比特),即两亿字节的向量,然后将这个16亿二进制位全部清零。对于每一个电子邮件地址X,用8个不同的随机数产生器(F1,F2,...,F8)产生8个信息指纹(f1,f2,...,f8)。再用一个随机产生器G把这8个信息指纹映射到1-16亿中的8个自然数g1,g2,...,g8(其实就是8个哈希函数)。现在把这8个位置的二进制全部设置为1。对这一亿个电子邮件地址都进行这样的处理后,一个针对这些电子邮件地址的布隆过滤器就建成了。如下图。另外,上面为何一亿个电子邮件地址需要建16亿二进制位和取8个哈希函数。这里推荐一篇非常有名的博文,地址为:https://blog.csdn.net/jiaomeng/article/details/1495500,里面有证明一个结论:想要保持错误率低,最好让位数组有一半还空着。即16亿个二进制位最多有8亿个二进制位被置为1,误识别率就会降到很低。
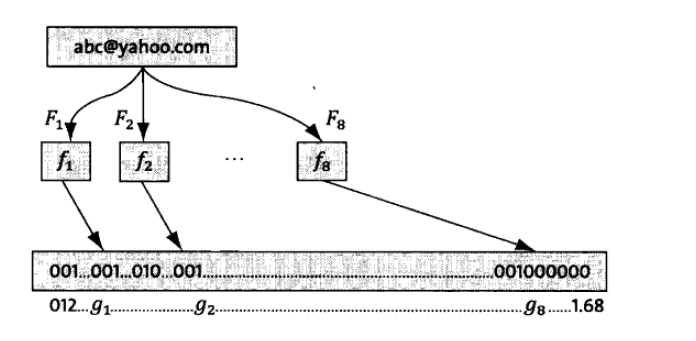
现在,让我们看看如何用布隆过滤器来监测一个可疑的电子邮件地址Y是否在黑名单中。用相同的8个随机产生器(F1,F2,...,F8)产生这个地址的8个信息指纹s1,s2,...,s8,然后将这个8个指纹对应到布隆过滤器的8个二进制位,分别为t1,t2,...,t8。如果Y在黑名单中,显然,t1,t2,...,t8对应的二进制数一定是1。这样,再遇到任何在黑名单中的电子邮件地址都能准确发现。布隆过滤器绝不会漏掉黑名单中的任何一个可疑地址。但是,它有一个不足之处。也就是它有极小的可能将一个不在黑名单中的电子邮件地址也判定为黑名单中,因为有可能某个好的邮件地址在布隆过滤器中对应的8个位置“恰巧”被(其他地址)设置为1。好在这种可能性很小。我们称之为误识别率。在上面的例子中,误识别率在万分之一以下。布隆过滤器的好处在于快速、省时间,但是有一定的误识别率。常见的补救办法是再建立一个小的白名单,存储那些可能被误判的邮件地址。
代码简单实现
#include <iostream> #include <vector> using namespace std; class Bitmap { public: Bitmap(size_t size) : size_(size) { bitVec_.resize((size_ >> 5) + 1); //多开辟一个空间,原因是数组只能表示区间[0,size) } void bitmapSet(int val) { int index = val >> 5; //相当于除以32,用移位操作可提高性能 int offset = val % 32; bitVec_[index] |= (1 << offset); } bool bitmapGet(int val) { int index = val >> 5; int offset = val % 32; return bitVec_[index] & (1 << offset); } private: size_t size_; vector<unsigned int> bitVec_; }; class BloomFilter { private: struct SimpleHash { SimpleHash() {} SimpleHash(size_t cap, size_t seed) : cap_(cap), seed_(seed) {} int hash(const std::string& s) { int result = 0; for (auto c : s) { result = result * seed_ + c; } return (cap_ - 1) & result; } private: size_t cap_; size_t seed_; }; enum { defaultSize = 100000000 * 16 }; //16亿 public: BloomFilter() { bitmap_ = new Bitmap(defaultSize); hashs_.reserve(seeds_.size()); for (int i = 0; i < seeds_.size(); ++i) { SimpleHash* hash = new SimpleHash(defaultSize, seeds_[i]); hashs_.push_back(hash); } } ~BloomFilter() { delete bitmap_; for (auto h : hashs_) { delete h; } } void add(const string& s) { for (auto h : hashs_) { bitmap_->bitmapSet(h->hash(s)); } } bool contain(const string& s) { bool ret = true; for (auto h : hashs_) { ret = ret && bitmap_->bitmapGet(h->hash(s)); } return ret; } private: std::vector<int> seeds_ = { 7, 11, 13, 31, 37, 61, 73, 97 }; //还不是随机生成 std::vector<SimpleHash*> hashs_; Bitmap* bitmap_; }; void bloomFilterTest() { std::string email = "1293173298@qq.com"; BloomFilter bf; bf.add(email); bool ret1 = bf.contain(email); bool ret2 = bf.contain("even.com"); } int main() { bloomFilterTest(); system("pause"); return 0; }