前言
半年前在极客时间订阅了王争的《数据结构和算法之美》,现在决定认真去看看。看到如何用快排思想在O(n)内查找第K大元素这一章节时发现王争对归并和快排的理解非常透彻,讲得也非常好,所以想记录总结一下。文章内容主要分析归并排序和快速排序原理,并根据它们共同的分治思想,引出如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素?
归并排序原理
核心思想:将数组从中间分成前后两部分,然后对前后两部分分别进行排序,再将排序好的两个部分有序合并在一起,这样整个数组有序。
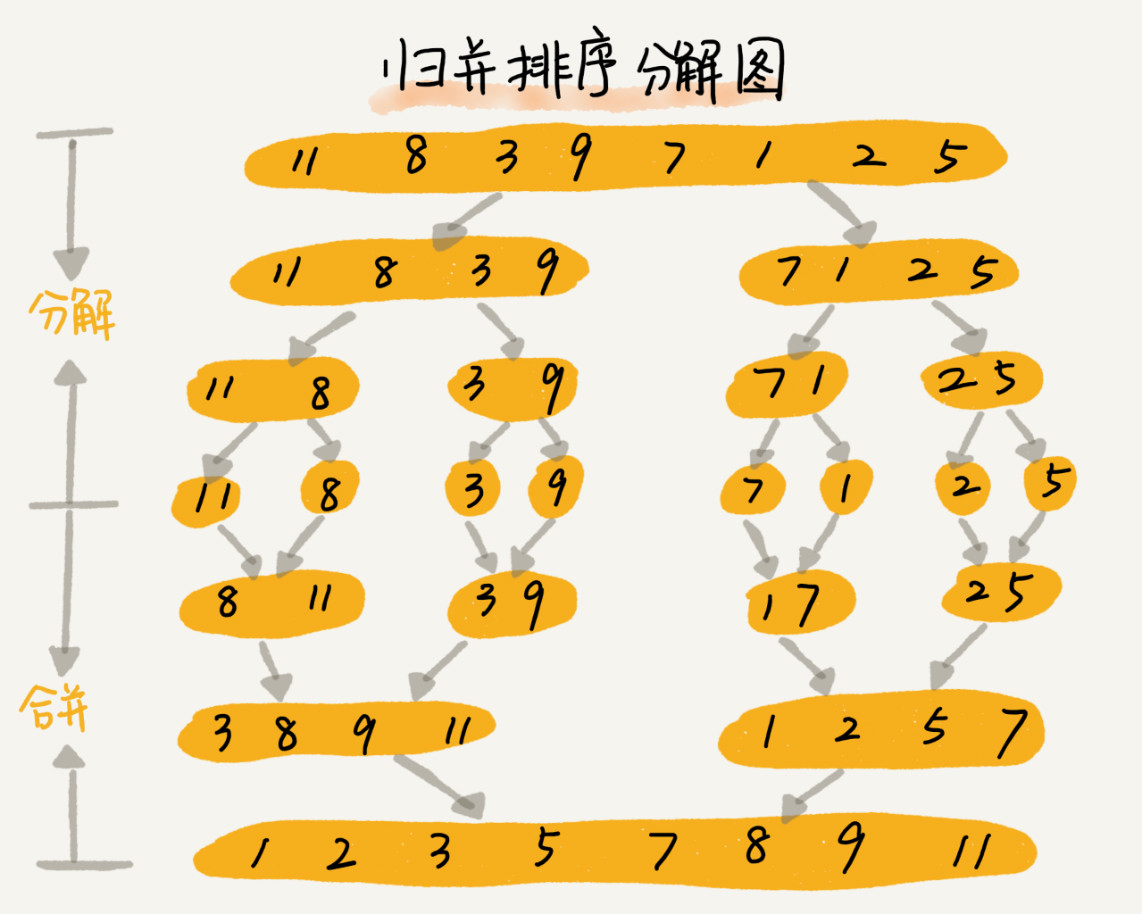
归并排序使用的就是分治思想。分治,顾名思义,就是分而治之,讲一个大的问题分解成小的问题来解决,小的问题解决了大的问题也就解决了。分治算法一般都是用递归来实现,分治是一种解决问题的处理思想,递归是一种编程技巧,两者并不冲突。以下重点讨论如何用递归代码来实现归并排序。下面是归并排序的递推公式。
递推公式: merge_sort(p...r) = merge(merge_sort(p...q), merge_sort(q+1...r)) 终止条件: p >= r 不用继续分解
具体解释如下:
merge_sort(p...r) 表示给下标从 p 到 r 之间的数组排序。将这个排序问题转化为两个子问题 merge_sort(p...q) 和merge_sort(q+1...r),其中 q 为 p 和 r 的中间位置,即(p+r)/2。当前后两个子数组排好序之后,再将它们合并在一起,这样下标从 p 到 r 之间的数据也就排序好了。
C语言代码实现:
// 归并排序算法, A 是数组,n 表示数组大小 void mergeSort(int *a, int n){ mergeSortC(a, 0, n-1); } // 递归调用函数 void mergeSortC(int *a, int left, int right){ // 递归终止条件 if (left >= right) return; int mid = left + (right - left)/2; mergeSortC(a, left, mid); mergeSortC(a, mid+1, right); merge(a, left, mid, right); } // 合并函数 void merge(int *a, int left, int mid, int right){ int i = left, j = mid+1, k = 0; int *tmp = new int[right-left+1]; // 申请一个大小为right-left+1临时数组 while (i <= mid && j <= right){ if(a[i] < a[j]) tmp[k++] = a[i++]; else tmp[k++] = a[j++]; } while (i <= mid) tmp[k++] = a[i++]; while (j <= right) tmp[k++] = a[j++]; for (i=0; i <= right-left; i++){ a[left+i] = tmp[i]; } delete[] tmp; }
归并排序的时间复杂度任何情况下都是 O(nlogn),看起来非常优秀(快速排序最坏情况系时间复杂度也是 O(n2))。但归并排序并没有像快排那样应用广泛,因为它有一个致命的“弱点”,那就是归并排序不是原地排序算法。原因是合并函数需要借助额外的存储空间,空间复杂度为 O(n)。
C++实现:
void merge(std::vector<int>& a, int left, int mid, int right) { int i = left; int j = mid + 1; int k = 0; std::vector<int> v(right - left + 1); while (i <= mid && j <= right) { v[k++] = a[i] < a[j] ? a[i++] : a[j++]; } while (i <= mid) { v[k++] = a[i++]; } while (j <= right) { v[k++] = a[j++]; } for (i = 0; i < v.size(); ++i) { a[left + i] = v[i]; } } void mergeSort(std::vector<int>& a, int left, int right) { if (left >= right) return; int mid = left + (right - left) / 2; mergeSort(a, left, mid); mergeSort(a, mid+1, right); merge(a, left, mid, right); } void mergeSort(std::vector<int>& a) { mergeSort(a, 0, a.size() - 1); }
快速排序原理
核心思想:选取一个基准元素(pivot,比 pivot 小的放到左边,比 pivot 大的放到右边,对 pivot 左右两边的序列递归进行以上操作。
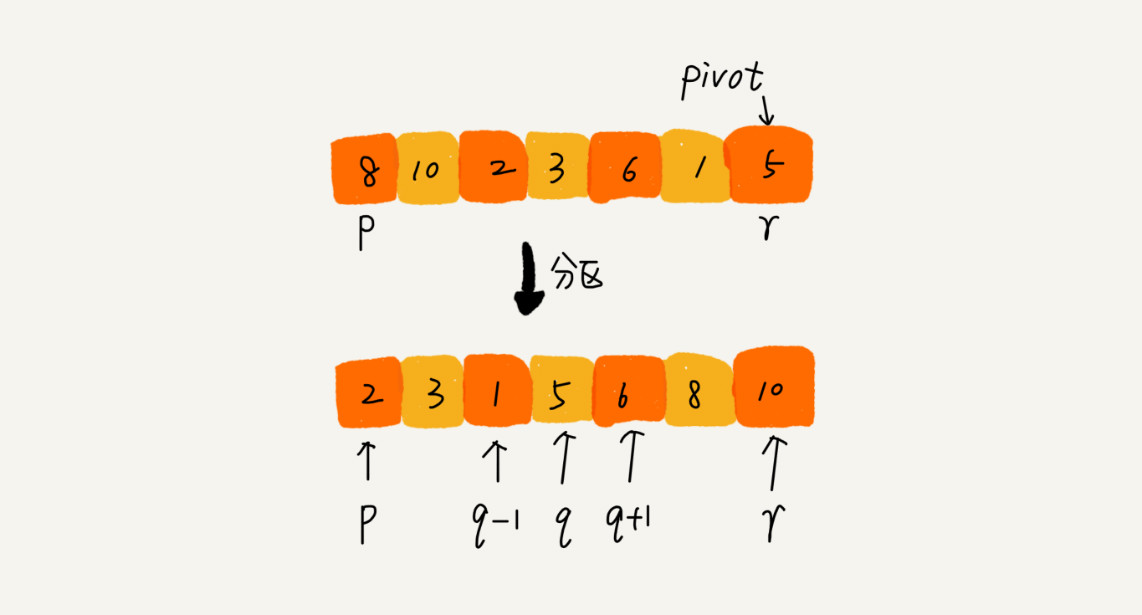
快速排序也是根据分治、递归的处理思想实现。地推公式如下:
递推公式: quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1...r) 终止条件: p >= r
C语言代码实现:
// 快速排序算法, A 是数组,n 表示数组大小 void quickSort(int *a, int n){ quickSortC(a, 0, n-1); } // 快排递归函数 void quickSortC(int *a, int left, int right){ // 递归终止条件 if (left >= right) return; // 获取分区点 int pivot = partition(a, left, right); quickSortC(a, left, pivot-1); quickSortC(a, pivot+1, right); } /* 原地分区函数,非常巧妙,以a[right]为基准,运算结果 * 是i前面的元素都小于pivot,i后面的元素大于等于pivot */ int partition(int *a, int left, int right){ int pivot = a[right]; int i = left; for (int j=left; j < right; j++){ if (a[j] < pivot){ swap(a[i], a[j]); i++; } } swap(a[i], a[right]); return i; }
快速排序的算法的平均时间复杂度是 O(nlogn),最坏时间复杂度是 O(n2),空间复杂度是O(1)。快速排序不是一个稳定的排序算法。
C++ 实现:
int partition(std::vector<int>& a, int left, int right) { using std::swap; int pivot = a[right]; int j = left; for (int i = left; i < right; ++i) { if (a[i] < pivot) swap(a[i], a[j++]); } swap(a[right], a[j]); return j; } void quickSort(std::vector<int>& a, int left, int right) { if (left >= right) return; int pivot = partition(a, left, right); quickSort(a, left, pivot-1); quickSort(a, pivot+1, right); } void quickSort(std::vector<int>& a) { quickSort(a, 0, a.size() - 1); }
归并排序和快速排序的区别
快排和归并用的都是分治思想,递归公式和代码都非常相似,但它们的区别在哪里呢?
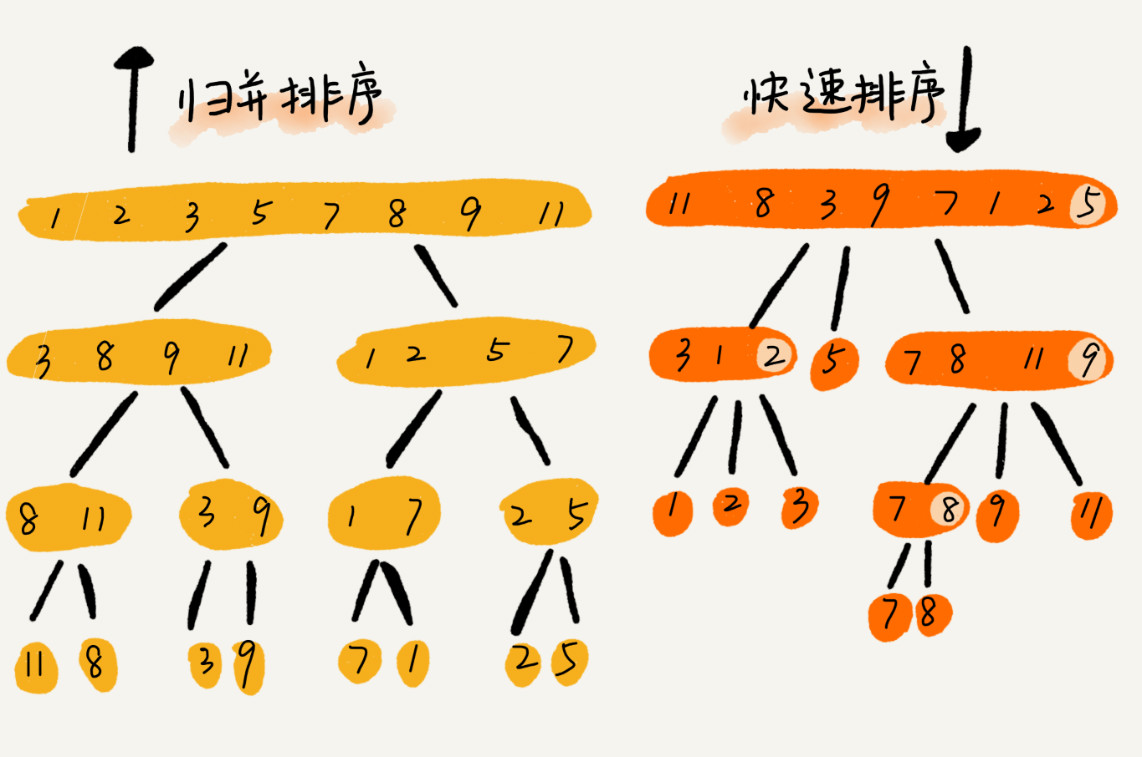
由上图可以发现,归并排序的处理过程是由下到上的,先处理子问题,然后合并。而快排正好相反,其处理过程是由上而下的,先分区,然后处理子问题。归并排序虽然是稳定的,时间复杂度是 O(nlogn)的排序算法,但它是非原地排序算法。快排通过设计巧妙的原地分区函数,可以实现原地排序,解决归并排序占用太多内存的问题。
第 K 大元素
快排核心思想就是分治和分区,我们可以利用分区的思想来求解开篇问题: O(n)时间复杂度内求无序数组中的第 K 大元素。
C语言代码实现:
// top K 算法, A 是数组,n 表示数组大小,k 表示第 k 大 int getTopK(int *a, int n, int k){ if (a == nullptr || n < k) return -1; return topK(a, 0, n-1, k); } int topK(int *a, int left, int right, int k){ int p = partition(a, left, right); if (k == p+1) return a[p]; if(k < p+1) return topK(a, left, p-1, k); else return topK(a, p+1, right, k); } /* 原地分区函数,非常巧妙,以a[right]为基准,运算结果 * 是i前面的元素都大于pivot,i后面的元素小于于等于pivot */ int partition(int *a, int left, int right){ int pivot = a[right]; int i = left; for (int j=left; j < right; j++){ if (a[j] > pivot){ swap(a[i], a[j]); i++; } } swap(a[i], a[right]); return i; }
LeetCode 215 C++实现:
class Solution { public: int partition(vector<int>& nums, int left, int right) { using std::swap; int pivot = nums[right]; int j = left; for (int i = left; i < right; ++i) { if (nums[i] > pivot) swap(nums[i], nums[j++]); } swap(nums[right], nums[j]); return j; } int getTopK(vector<int>& nums, int left, int right, int k) { if (left >= right) return nums[left]; int pivot = partition(nums, left, right); if (pivot + 1 == k) return nums[pivot]; return (pivot + 1 < k) ? getTopK(nums, pivot+1, right, k) : getTopK(nums, left, pivot-1, k); } int findKthLargest(vector<int>& nums, int k) { return getTopK(nums, 0, nums.size() - 1, k); } };