K-Means原理及代码实现

对于有监督学习，我们知道其训练数据形式为(T=left { (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),cdots ,(x^{(n)},y^{(n)}) ight })，其中，(x)表示样本实例，(y)表示样本所属类别。而对于无监督学习，训练数据不提供对应的类别，训练数据形式为(T=left { (x^{(1)}),(x^{(2)}),cdots ,(x^{(n)}) ight })。这里，对无监督的聚类算法K-Means进行总结。

1 K-Means原理

K-Means作为聚类算法是如何完成聚类的呢？正如其算法名称，(K)表示簇的个数，Means表示均值。(注： 在聚类中，把数据所在的集合称为簇)。K-Means算法的基本思想是将训练数据集按照各个样本到聚类中心的距离分配到距离较近的(K)个簇中，然后计算每个簇中样本的平均位置，将聚类中心移动到该位置。

根据上面K-Means算法的基本思想，K-Means算法可以总结成两步：
- 簇分配：样本分配到距离较近的簇
- 移动聚类中心：将聚类中心移动到簇中样本平均值的位置

假设有(K)个簇((C_{1},C_{2},cdots ,C_{k}))，样本距离簇类中心的距离的表达式为：

[sum_{i=1}^{k}sum_{xepsilon C_{i}}left | x-mu _{i} ight |^{2} ]

其中(C_{i})是第1到(K)个最接近样本(x)的聚类中心，(mu _{i})是该簇(C_{i})中所有样本点的均值组成的向量。(mu _{i})的表达式为：

[mu _{i}=frac{1}{|C_{i}|}sum_{xepsilon C_{i}}x ]

举例，如何计算(mu _{2})的聚类中心？假设被分配到了聚类中心2的4个样本有：(x^{(1)})，(x^{(5)})，(x^{(6)})，(x^{(10)})，也就是(C_{(1)}=2)，(C_{(5)}=2)，(C_{(6)}=2)，
(C_{(10)}=2)，

[mu _{2}=frac{1}{4}left [ x^{(1)}+x^{(5)}+x^{(6)}+x^{(10)} ight ]epsilon mathbb{R}^{n} ]

(n)表示样本的特征个数。

2 K-Means算法

K-Means算法： 簇分配和移动聚类中心

输入: (T=left { x^{(1)},x^{(2)},cdots ,x^{(m)} ight })，(K)

step1 随机初始化(K)个聚类中心(mu _{1},mu _{2},cdots ,mu _{k}epsilon mathbb{R}^{n})

step2 计算各个样本点到聚类中心的距离，如果样本距离第(i)个聚类中心更近，将其分配到第(i)簇

step3 计算每个簇中所有样本点的平均位置，将聚类中心移动到该位置

step4 重复2-3直至各个聚类中心的位置不再发生变化

3 K-Means代码实现

簇分配+移动聚类中心

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat

#簇分配 将每一个训练样本分配给最接近的簇中心
def findClosestCentroids(X, centroids):
    """
    output a one-dimensional array idx that holds the
    index of the closest centroid to every training example.
    """
    idx = []
    max_dist = 1000000  # 限制一下最大距离
    for i in range(len(X)):
        minus = X[i] - centroids  # here use numpy's broadcasting
        dist = minus[:,0]**2 + minus[:,1]**2
        if dist.min() < max_dist:
            ci = np.argmin(dist)
            idx.append(ci)
    return np.array(idx)


mat = loadmat('D:/Python/Andrew-NG-Meachine-Learning/machine-learning-ex7/ex7/ex7data2.mat')  
X = mat['X']
#print(X.shape)  #(300, 2)
init_centroids = np.array([[3, 3], [6, 2], [8, 5]]) #自定义一个centroids,[3, 3], [6, 2], [8, 5]
idx = findClosestCentroids(X, init_centroids)
#print(idx) #[0 2 1 ..., 1 1 0]
#print(idx.shape) #(300,)
print(idx[0:3])   #[0 2 1]  计算idx[0:3] 也就是前三个样本所属簇的索引或者序号

#移动聚类中心 重新计算每个簇中心—这个簇中所有点位置的平均值  

def computeCentroids(X, idx):
    centroids = []
    for i in range(len(np.unique(idx))):  # np.unique() means K
        u_k = X[idx==i].mean(axis=0)  # 求每列的平均值
        centroids.append(u_k)
        
    return np.array(centroids)

print(computeCentroids(X, idx))

#输出

[[ 2.42830111  3.15792418]
[ 5.81350331  2.63365645]
[ 7.11938687  3.6166844 ]]

#kmeans on an example dataset
def plotData(X, centroids, idx=None):
    """
    可视化数据，并自动分开着色。
    idx: 最后一次迭代生成的idx向量，存储每个样本分配的簇中心点的值
    centroids: 包含每次中心点历史记录
    """
    colors = ['b','g','gold','darkorange','salmon','olivedrab',
              'maroon', 'navy', 'sienna', 'tomato', 'lightgray', 'gainsboro'
             'coral', 'aliceblue', 'dimgray', 'mintcream', 'mintcream']
    
    assert len(centroids[0]) <= len(colors), 'colors not enough '
      
    subX = []  # 分号类的样本点
    if idx is not None:
        for i in range(centroids[0].shape[0]):
            x_i = X[idx == i]
            subX.append(x_i)

    else:
        subX = [X]  # 将X转化为一个元素的列表，每个元素为每个簇的样本集，方便下方绘图
    
    # 分别画出每个簇的点，并着不同的颜色
    plt.figure(figsize=(8,5))    
    for i in range(len(subX)):
        xx = subX[i]
        plt.scatter(xx[:,0], xx[:,1], c=colors[i], label='Cluster %d'%i)
    plt.legend()
    plt.grid(True)
    plt.xlabel('x1',fontsize=14)
    plt.ylabel('x2',fontsize=14)
    plt.title('Plot of X Points',fontsize=16)
    
    # 画出簇中心点的移动轨迹
    xx, yy = [], []
    for centroid in centroids:
        xx.append(centroid[:,0])
        yy.append(centroid[:,1])
    
    plt.plot(xx, yy, 'rx--', markersize=8)
                         
plotData(X, [init_centroids])

运行效果：

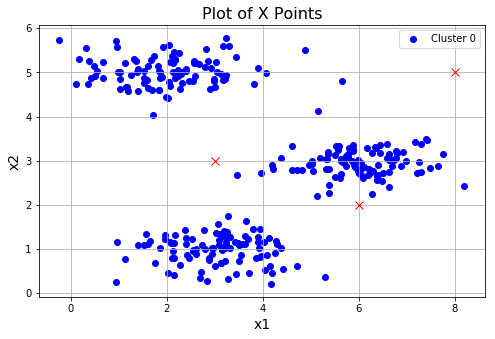
查看聚类中心移动效果

def runKmeans(X, centroids, max_iters):
    K = len(centroids)
    
    centroids_all = []
    centroids_all.append(centroids)
    centroid_i = centroids
    for i in range(max_iters):
        idx = findClosestCentroids(X, centroid_i)
        centroid_i = computeCentroids(X, idx)
        centroids_all.append(centroid_i)
        
    return idx, centroids_all

idx, centroids_all = runKmeans(X, init_centroids, 20)
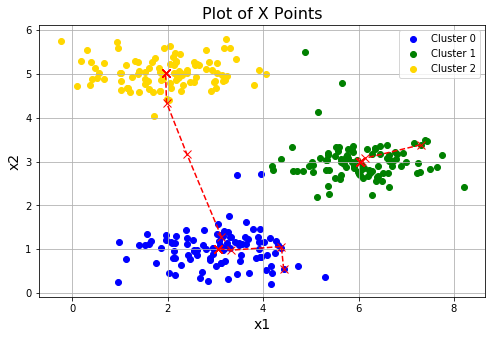
plotData(X, centroids_all, idx)

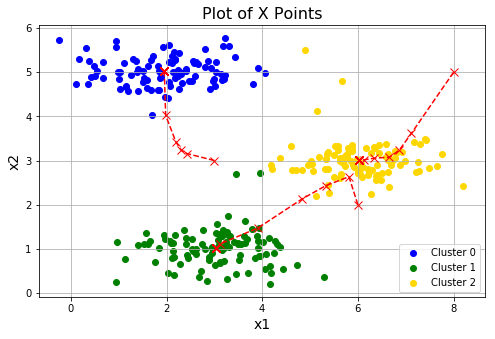
对簇中心点进行初始化的一个好的策略就是从训练集中选择随机的例子。

随机初始化簇中心

def initCentroids(X, K):
    """随机初始化"""
    m, n = X.shape
    idx = np.random.choice(m, K)
    centroids = X[idx]
    return centroids

#进行三次随机初始化，看下各自的效果。会发现第三次的效果并不理想，这是正常的，落入了局部最优
for i in range(3):
    centroids = initCentroids(X, 3)
    idx, centroids_all = runKmeans(X, centroids, 10)
    plotData(X, centroids_all, idx)

进行三次随机初始化，看下各自的效果。看到第三次的效果并不理想，都落入了局部最优。

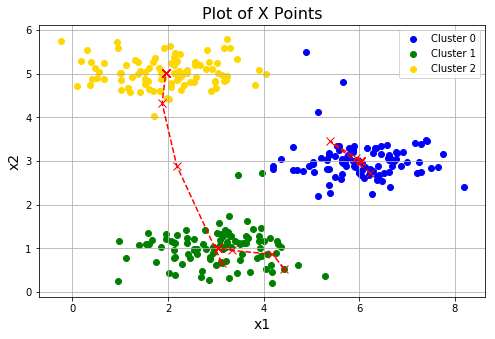
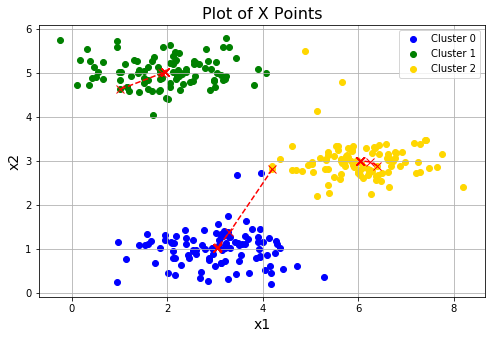
用K-Means进行图像压缩, 通过减少图像中出现的颜色的数量 ，只剩下那些在图像中最常见的颜色。

K-Means图像压缩

from skimage import io
import matplotlib.pyplot as plt


A = io.imread('D:/Python/Andrew-NG-Meachine-Learning/machine-learning-ex7/ex7/bird_small.png')
print(A.shape)  #(128, 128, 3)
plt.imshow(A)
A = A/255   #Divide by 255 so that all values are in the range 0-1


X = A.reshape(-1, 3)
K = 16    
centroids = initCentroids(X, K)
idx, centroids_all = runKmeans(X, centroids, 10)


img = np.zeros(X.shape)
centroids = centroids_all[-1]
for i in range(len(centroids)):
    img[idx == i] = centroids[i]
    
img = img.reshape(128, 128, 3)
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(A)
axes[1].imshow(img)

参考：吴恩达机器学习 吴恩达机器学习作业Python实现