manacher算法可以解决字符串的回文子串长度问题。
个人感觉szy学长讲的非常好,讲过之后基本上就理解了。
那就讲一下个人的理解。(参考了szy学长的ppt)
如果一个回文子串的长度是偶数,对称轴会落在两个字符中间。
首先两个字符中间的这个位置就很难表示。
所以我们在两个字符中间加上没有用的字符,比如说'#'。开头结尾也加上。
例如:abcba --> #a#b#c#b#a#
这样我们能很方便的表示每一个位置。
manacher算法最终的目的是求出一个数组pl[i],代表以i为回文中心(也就是对称轴)的最长回文子串的回文半径。
回文半径指的是回文子串的长度除以二之后向上取整。
比如:#a#b#a#的回文半径就是4。
考虑用递推的方法求出pl数组。
首先我们知道pl[1]=1(特殊记一下)。
在递推的过程中维护一个np表示使i+pl[i]最大的一个i。
计算f[i]的时候,先考虑使用已知的信息求出f[i]。
如果i<=np+pl[np],意味着i被以np为回文中心的最长回文子串“覆盖”了。
下面的图用红色表示以np为回文中心的最长回文子串,用绿色表示以i为回文中心的最长回文子串。
这时有两种情况:
1.不仅i被覆盖,以i为回文中心的最长回文子串也被完全覆盖了。

这个时候由于对称性,pl[i]=pl[2*np-i]。
2.虽然i被覆盖,但是以i为回文中心的最长回文子串没有被完全覆盖。
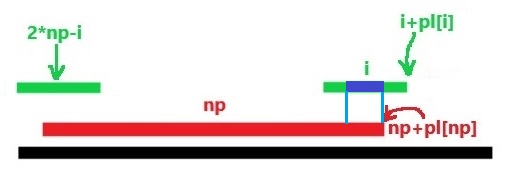
这个时候我们只能保证np+pl[np]以内的对称性(蓝色部分)。
也就是说,pl[i]=pl[np]+np-i。
我们并不知道是哪种情况,所以只能对这两种情况分别求值并取其中的最小值。
之后如果还能继续向外拓展回文部分,就类似暴力的做法,一下一下向外拓展。
最后更新一下np。
求出的pl是适用于新串的(就是混了一堆‘#’的那个串)。
不难发现,对于原串,以i为中心的最长回文子串的长度为pl[i]-1,这个串的开始位置为(i-pl[i])/2+1(向下取整)。
来一道模板题练练:洛谷 P3805 【模板】manacher算法
这里不得不说,szy学长给的代码真是又简洁又明了。
吊打网上那些参杂各种特判的冗长又难读的代码。
膜拜orz。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 6 int n; 7 char a[11000005]; 8 char s[22000005]; 9 int pl[22000005]; 10 11 int main() 12 { 13 scanf("%s",a+1); 14 int al=strlen(a+1); 15 for(int i=1;i<=al;i++) 16 s[++n]='#',s[++n]=a[i]; 17 s[++n]='#'; 18 int np=1; 19 pl[1]=1; 20 for(int i=2;i<=n;i++) 21 { 22 pl[i]=min(pl[2*np-i],pl[np]+np-i); 23 for(;i+pl[i]<=n&&s[i+pl[i]]==s[i-pl[i]];pl[i]++); 24 if(i+pl[i]>np+pl[np])np=i; 25 } 26 int ans=0; 27 for(int i=1;i<=n;i++)ans=max(ans,pl[i]-1); 28 printf("%d",ans); 29 return 0; 30 }