散列表
概述
散列表Hash Table来源于数组,它借助散列函数对数组这种数据结构进行扩展,利用的是数组支持按照下标随机访问元素的特性。
需要存储在散列表中的数据我们称为键key,将键转化为数组下标的方法hash(key)称为散列函数,散列函数的计算结果称为散列值。
将数据存储在散列值对应的数组下标位置。
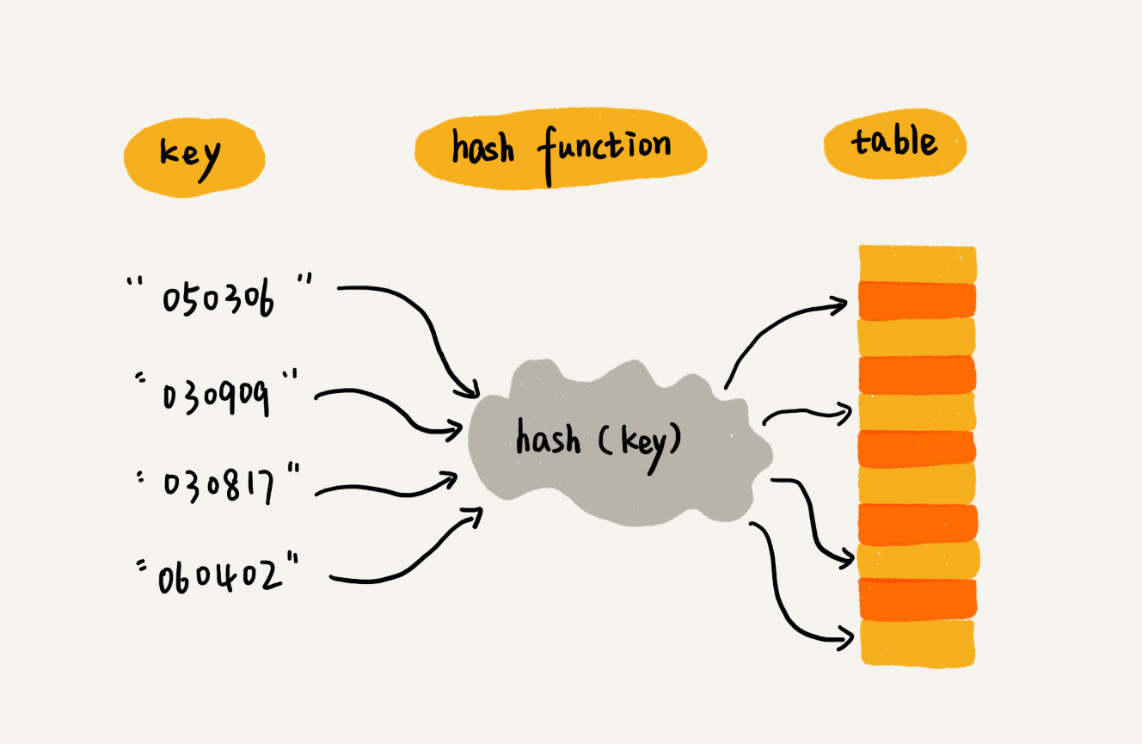
设计散列函数
设计散列函数的基本要求
散列函数计算得到的散列值是一个非负整数。
若key1=key2,则hash(key1)=hash(key2)。
若key≠key2,则hash(key1)≠hash(key2)。
当空闲位置越来越少,散列值冲突的概率越来越大,也就无法满足第三条。
散列冲突的解决方法
开放寻址法
出现散列冲突就往下探测数组空间直到找到空闲位置将key插入。
线性探测
开放寻址法会导致占用删除元素的位置,这样会导致原来的算法失效。
所以线性探测法的删除操作是将要删除的元素标记为deleted,当要插入数据时遇到这种位置就继续向下探测。
二次探测
线性探测法每次探测的步长为1,即在数组中一个一个探测,比如hash(key)+1,hash(key)+2...
而二次探测的步长变为原来的平方hash(key)+1^2,hash(key)+2^2...。
双重散列
使用一组散列函数,先使用第一个,如果有冲突就换下一个,直到找到空闲位置为止。
性能描述
我们使用装载因子来表示空位多少:
散列表的装载因子 = 填入表中的元素个数 / 散列表的长度
装载因子越大,说明空闲位置越少,冲突越多,散列表的性能会下降。
链表法
插入数据
当插入的时候,我们需要通过散列函数计算出对应的散列槽位,将其插入到对应的链表中即可,所以插入的时间复杂度为O(1)。
查找或删除数据
对于散列比较均匀的散列函数,链表的节点个数k=n/m,其中n表示散列表中数据的个数,m表示散列表中槽的个数
当查找、删除一个元素时,通过散列函数计算对应的槽,然后遍历链表查找或删除,两操作与链表长度k成正比,即时间复杂度为O(k)。

思考
假设我们有10万条URL访问日志,如何按照访问次数给URL排序
遍历10万条URL记录,URL为key,声明一个记录访问次数的字段count,存入散列表,每次遇到重复的就累加count,
最后对count进行桶排序或者快速排序。
有两个字符串数组,每个数组大约有10万条字符串,如何快速找出两个数组中相同的字符串
将其中一个数组以数组成员为key存到散列表中,每个字符串标记一个value=0,
再以第二个数组的成员进行查询,查询得到一样得的就累加,最后根据value>0这个条件找到这些字符串。