分治思想
分治思想
分治,顾明思意就是分而治之,将一个大问题分解成小的子问题来解决,小的子问题解决了,大问题也就解决了。
分治与递归的区别
分治算法一般都用递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧。
归并排序
算法原理
归并的思想
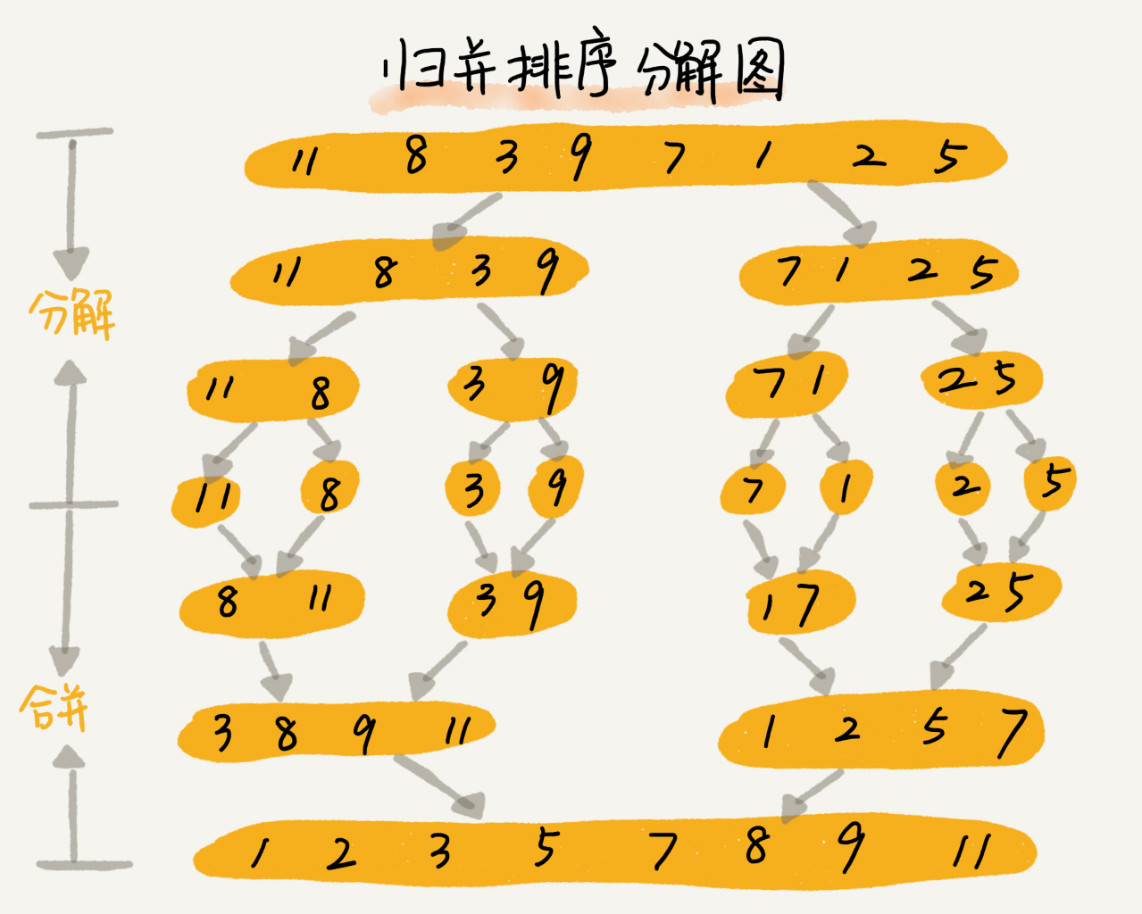
先把数组从中间分成前后两部分,然后对前后两部分分别进行排序,
再将排序好的两部分合并到一起,这样整个数组就有序了。
这就是归并排序的核心思想。如何用递归实现归并排序呢?
写递归代码的技巧就是分写得出递推公式,然后找到终止条件,最后将递推公式翻译成递归代码。
递推公式
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件
p >= r 不用再继续分解
代码实现
public static void MergeSort(int[] data,int n){ //传入数组、索引0和最后一位的索引 Merge_c(data, 0, n - 1); } public static void Merge_c(int[] data,int p,int r){ //递归终止条件:p与r相等或p大于r即细分到每个数据成员 if (p >= r) return; //定义q为中间值 int q = (p + r) / 2; //对q和中间值、中间值和r继续细分 Merge_c(data,p,q); Merge_c(data,q+1,r); //直到细分到每个数据成员返回后,开始两两合并 Merge(data,p,q,r); } public static void Merge(int[] data,int front,int mid,int back){ //定义data数组中第front到mid的数组组成的数组 int[] frontArray = new int[mid + 1]; for (int n = front; n < frontArray.Length; n++) frontArray[n] = data[n]; //定义data数组中第mid到back的数组组成的数组 int[] backArray = new int[back - mid]; for (int n = mid; n < backArray.Length; n++) backArray[n] = data[n]; //定义临时数组,长度为数组中第front到back间的数据的长度 int[] temp = new int[back - front + 1]; //定义三个临时变量作为游标,分别初始化为front和mid+1,以及临时数组中的最后一个数据的位置为0 int i = front, j = mid+1, k = 0; //循环直到i超过了mid或者j超过了back while(i<=mid&&j<=back){ //根据大小,将data的第i/j的数据存入temp数组 if (data[i] < data[j]) temp[k++] = data[i++]; else temp[k++] = data[j++]; } //定义两个临时变量为记录起始位置,初始化为合并的两数组中的前一个数组的头尾索引 int start = i, end = mid; //如果是后一个数组没有遍历完,就改为后一个数组的头尾索引 if (j <= back){ start = j; end = back; } //将未遍完的数组剩余的数据存入temp数组 while (start <= end) temp[k++] = data[start++]; //将完成排序的temp数组合并到对应的data数组位置 for (int l = 0; l < temp.Length; l++) data[front + l] = temp[l]; }
性能分析
算法稳定性
归并排序是一种稳定排序算法。
时间复杂度
归并排序的时间复杂度是O(nlogn)。
空间复杂度
归并排序算法不是原地排序算法,空间复杂度是O(n)
因为归并排序的合并函数,在合并两个数组为一个有序数组时,需要借助额外的存储空间
快速排序
算法原理
快排的思想
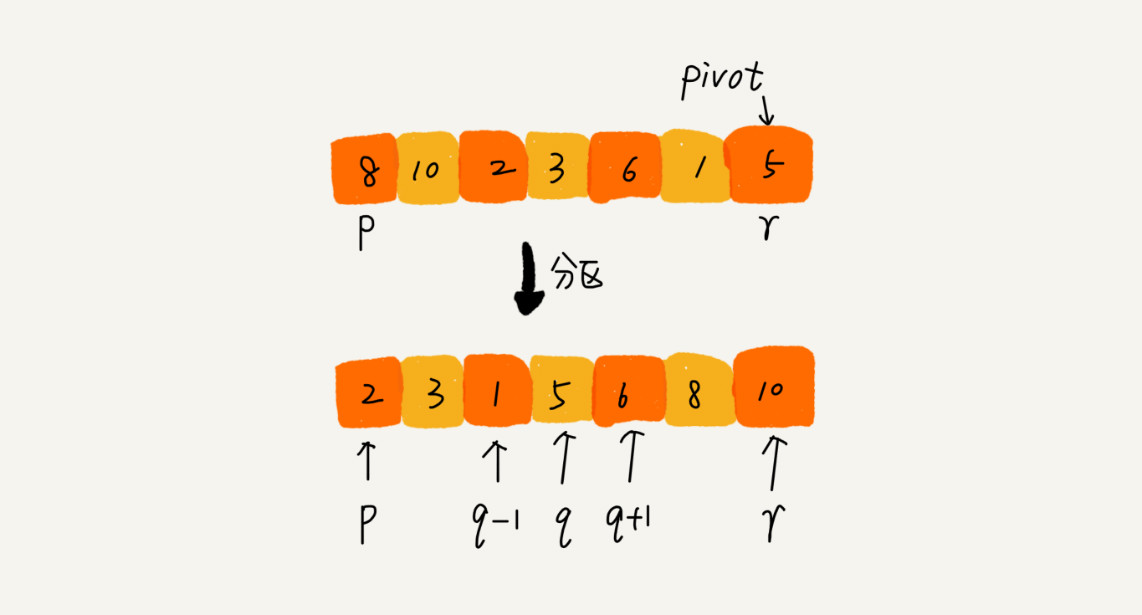
如果要排序数组中下标从p到r之间的一组数据,我们选择p到r之间的任意一个数据作为pivot(分区点)。
然后遍历p到r之间的数据,将小于pivot的放到左边,将大于pivot的放到右边,将povit放到中间。
经过这一步之后,数组p到r之间的数据就分成了3部分,前面p到q-1之间都是小于povit的,中间是povit,后面的q+1到r之间是大于povit的。
根据分治、递归的处理思想,我们可以用递归排序下标从p到q-1之间的数据和下标从q+1到r之间的数据,直到区间缩小为1,就说明所有的数据都有序了。
递推公式
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)
终止条件
p >= r
代码实现
专栏写的快排拆成三个方法让人头疼,我用C#改写了群里算法大佬用c写的快排,简单明了。
public static void QuickSort(int[] data,int front,int back) { //定义头尾索引、分区点 int i = front, j = back, mid = data[front + (back - front) / 2]; //循环到i大于j while (i <= j) { //头尾索引步进 while (data[i] < mid) i++; while (data[j] > mid) j--; //i指向mid左侧,j仍指向mid右侧,就交换二者位置,使mid左侧元素比其小,右侧比其大 if (i <= j) { int temp = data[i]; data[i] = data[j]; data[j] = temp; i++;j--; } } //循环结束后mid左侧是比他小的,右侧是比他大的。 //对左右两侧递归排序,直到范围为一个数 if (i < back) QuickSort(data,i, back); if (front < j) QuickSort(data,front, j); }
性能分析
算法稳定性
快速排序是不稳定的排序算法。
时间复杂度
如果每次分区操作都能正好把数组分成大小接近相等的两个小区间,
那快排的时间复杂度递推求解公式跟归并的相同。快排的时间复杂度也是O(nlogn)。
如果数组中的元素原来已经有序了,快排的时间复杂度就是O(n^2)。
前面两种情况,一个是分区及其均衡,一个是分区极不均衡,
它们分别对应了快排的最好情况时间复杂度和最坏情况时间复杂度。
T(n)大部分情况下是O(nlogn),只有在极端情况下才是退化到O(n^2)。
空间复杂度
快排是一种原地排序算法,空间复杂度是O(1)
归并排序与快速排序的区别
归并排序
先递归调用,再进行合并,合并的时候进行数据的交换。所以它是自下而上的排序方式。
何为自下而上?就是先解决子问题,再解决父问题。
快速排序
先分区,在递归调用,分区的时候进行数据的交换。所以它是自上而下的排序方式。
何为自上而下?就是先解决父问题,再解决子问题。
思考
O(n)时间复杂度内求无序数组中第K大元素
有10个访问日志文件,每个日志文件大小约为300MB,每个文件里的日志都是按照时间戳从小到大排序的。现在需要将这10个较小的日志文件合并为1个日志文件,合并之后的日志仍然按照时间戳从小到大排列。如果处理上述任务的机器内存只有1GB,你有什么好的解决思路能快速地将这10个日志文件合并