设定有三个柱A,B,C,目标是将A上面的盘子全部移动到C上面(合法移动)
递归算法
这是一道递归方法的经典题目,乍一想还挺难理清头绪的,我们不妨先从简单的入手。
假设 n = 1,只有一个盘子,很简单,直接把它从 A 中拿出来,移到 C 上;
如果n = 2 呢?这时候我们就要借助 B 了,因为小盘子必须时刻都在大盘子上面,共需要 4 步。
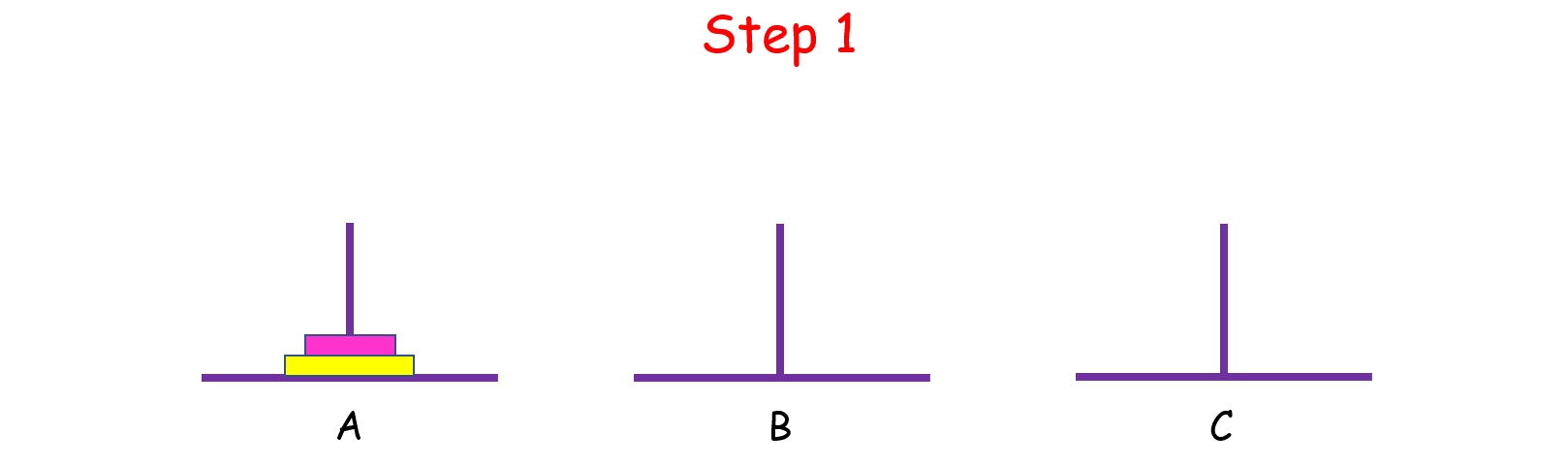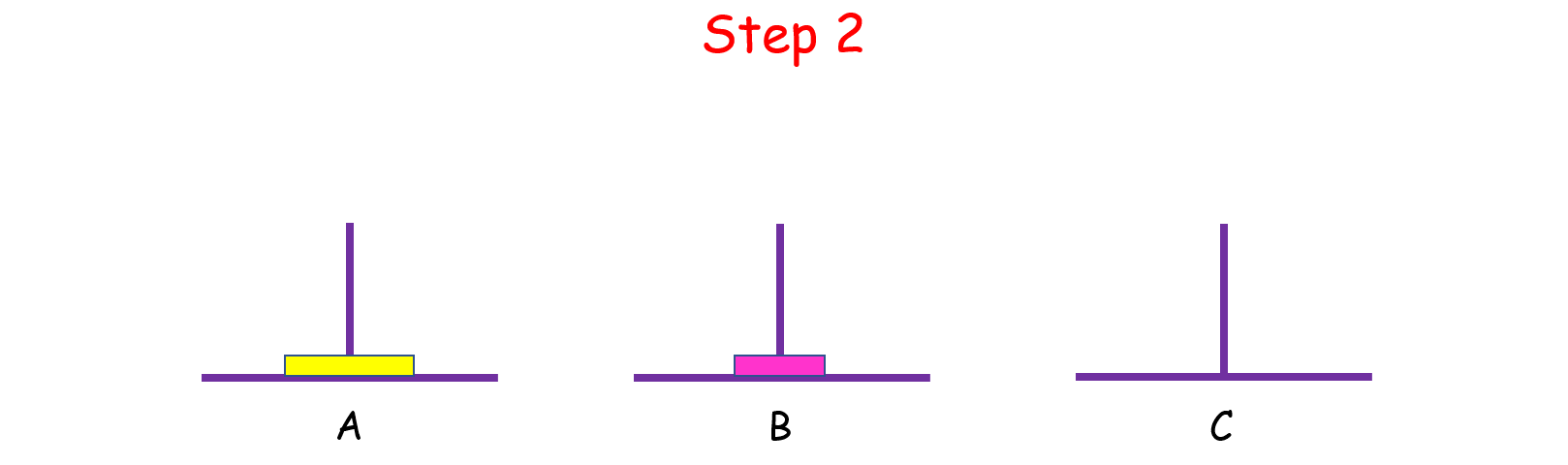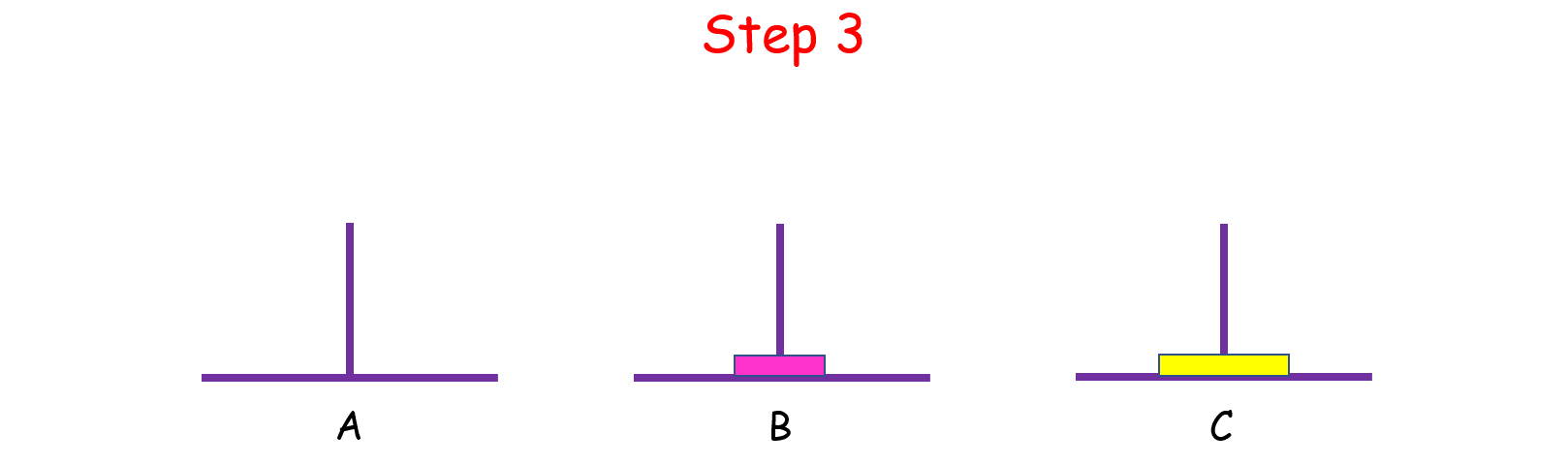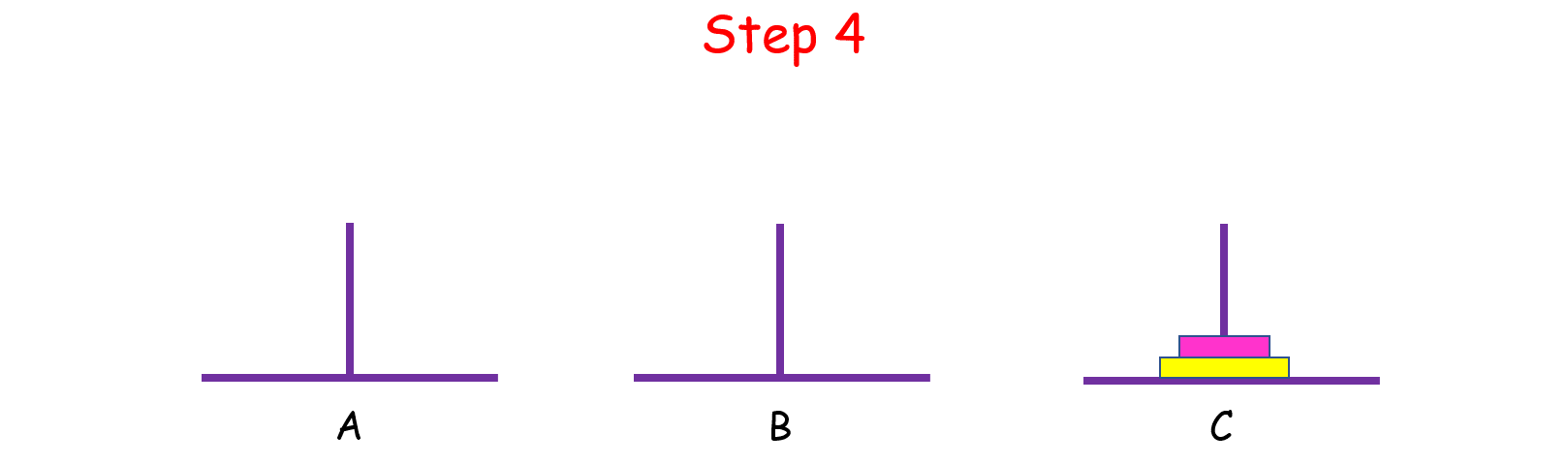
如果 n > 2 呢?思路和上面是一样的,我们把 n 个盘子也看成两个部分,一部分有 1 个盘子,另一部分有 n - 1 个盘子。
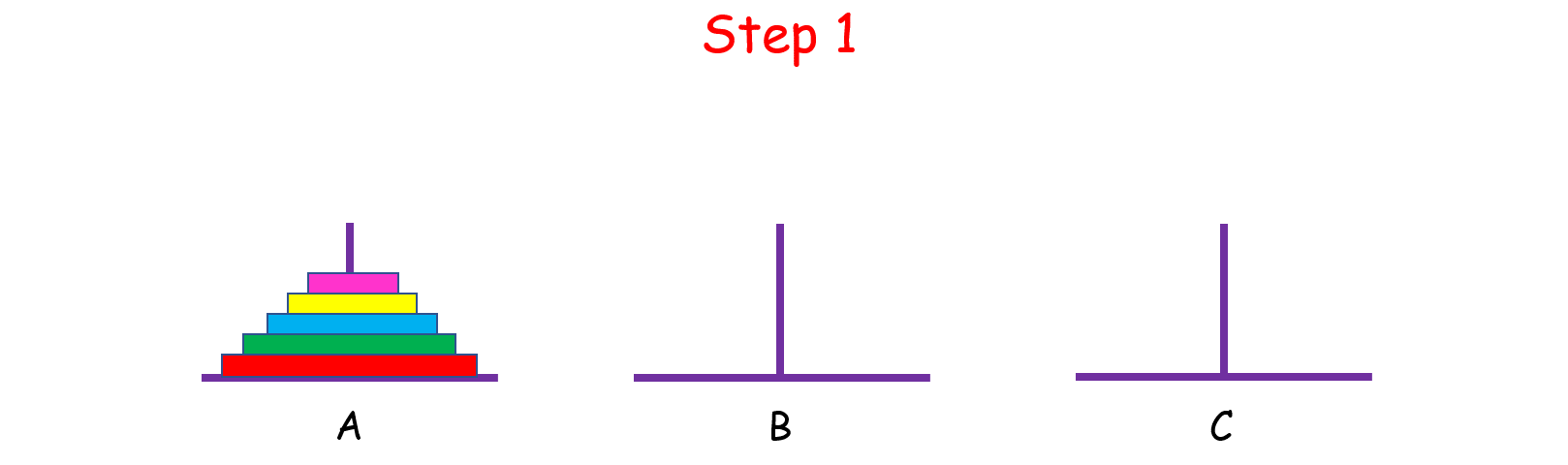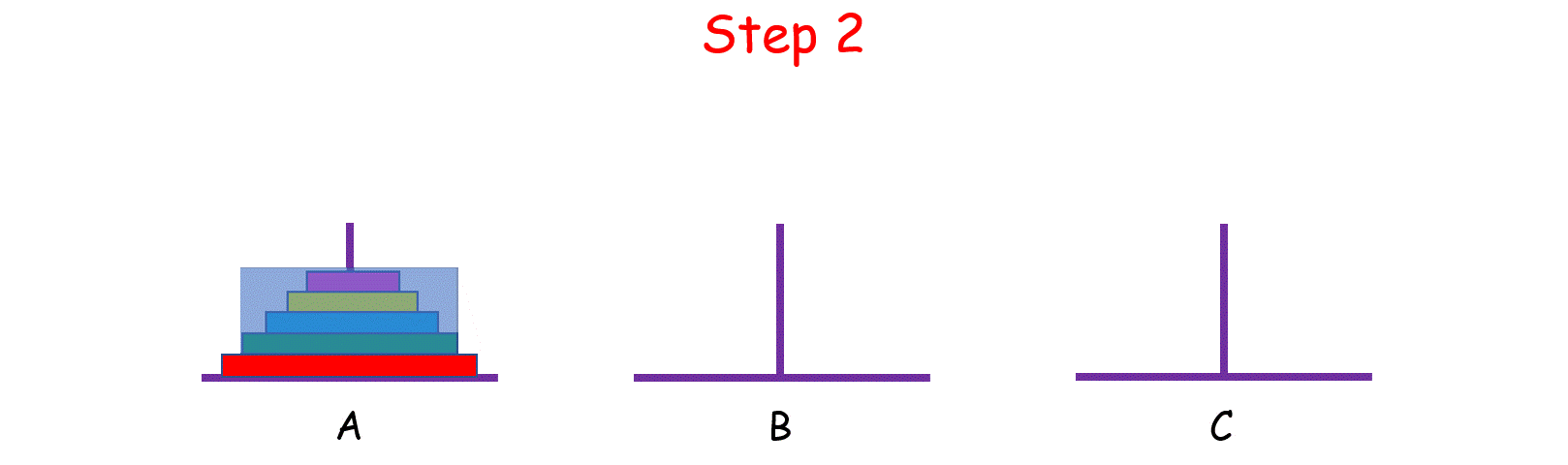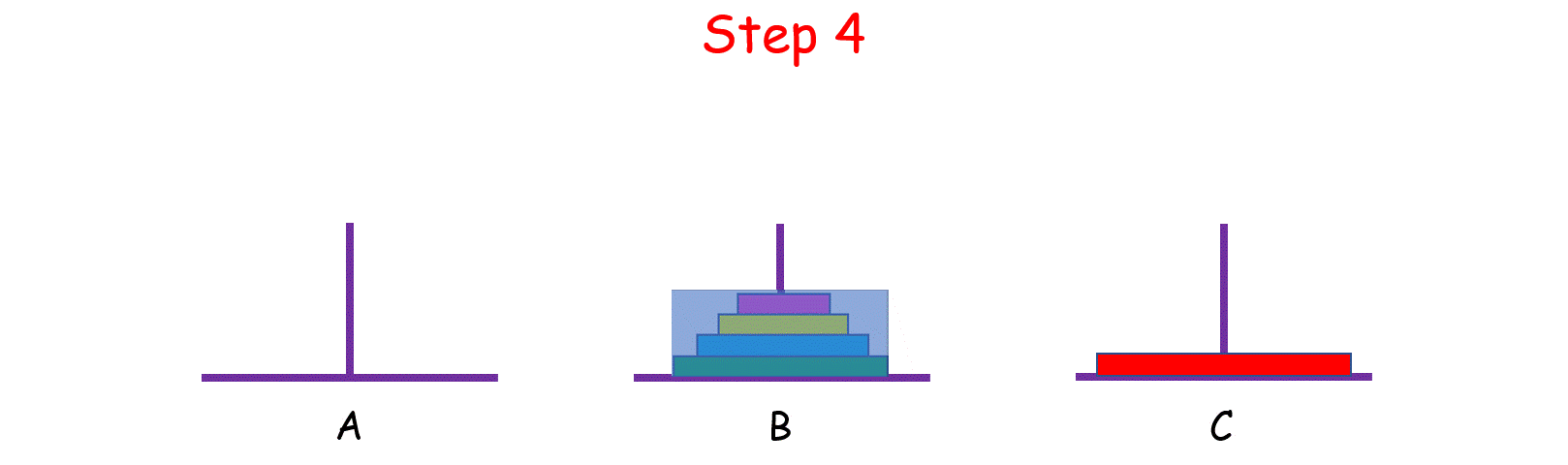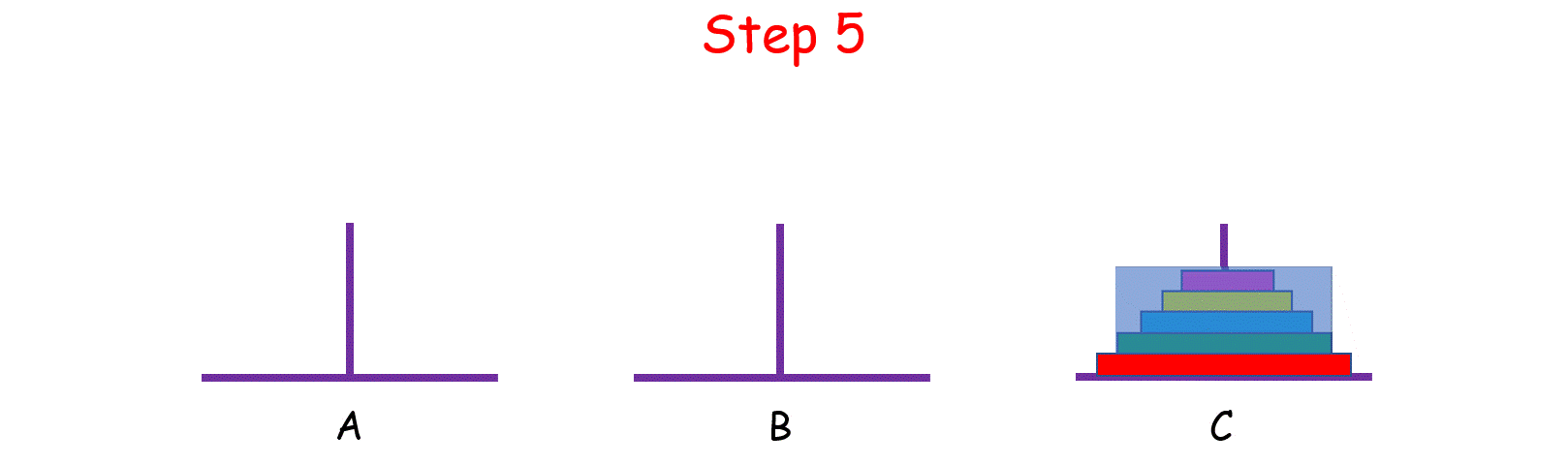
观察上图,你可能会问:“那 n - 1 个盘子是怎么从 A 移到 C 的呢?”
注意,当你在思考这个问题的时候,就将最初的 n 个盘子从 A 移到 C 的问题,转化成了将 n - 1 个盘子从 A 移到 C 的问题, 依次类推,直至转化成 1 个盘子的问题时,问题也就解决了。这就是分治的思想。
而实现分治思想的常用方法就是递归。不难发现,如果原问题可以分解成若干个与原问题结构相同但规模较小的子问题时,往往可以用递归的方法解决。具体解决办法如下:
- n = 1 时,直接把盘子从 A 移到 C;
- n > 1 时,
先把上面 n - 1 个盘子从 A 移到 B(子问题,递归);
再将最大的盘子从 A 移到 C;
再将 B 上 n - 1 个盘子从 B 移到 C(子问题,递归)。
代码实现
List实现
public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
move(A.size(), A, B,C);
}
public void move(int n,List<Integer> A, List<Integer> B, List<Integer> C){
if (n == 1){
C.add(A.get(A.size()-1));
A.remove(A.size()-1);
return;
}
//从A->B
move(n-1, A, C, B);
//从A->C
C.add(A.get(A.size()-1));
A.remove(A.size()-1);
//从B->C
move(n-1, B, A, C);
}
栈实现
public static void hanota(Stack<Integer> A, Stack<Integer> B, Stack<Integer> C) {
move(A.size(), A, B,C);
}
public static void move(int n, Stack<Integer> A, Stack<Integer> B, Stack<Integer> C){
if (n == 1){
//A->C
C.push(A.pop());
return;
}
//从A->B
move(n-1, A, C, B);
//从A->C
C.push(A.pop());
//从B->C
move(n-1, B, A, C);
}
算法分析
- 时间复杂度:O(2^n-1)一共需要移动的次数。
- 空间复杂度:O(1)。
非递归算法
找规律
请3步一组观察规律:
数量为3时:
1. A->C
2. A->B
3. C->B
4. A->C
5. B->A
6. B->C
7. A->C
数量为4时:
1. A->B
2. A->C
3. B->C
4. A->B
5. C->A
6. C->B
7. A->B
8. A->C
9. B->C
10. B->A
11. C->A
12. B->C
13. A->B
14. A->C
15. B->C
自行观察规律,然后看完算法和代码后验证一遍规律
规律
当盘子数为奇数时:
依次按照下面顺序进行合法的交换,直到C上盘子数=总盘子数
A C
A B
B C
当盘子数为偶数时:
依次按照下面顺序进行合法的交换,直到C上盘子数=总盘子数
A B
A C
B C
算法实现原理
Algorithm:
While size of Destination is less not equal to n
do
{
If num of disks is even then
Make legal move between Source and Auxilary
Make the legal move between pegs Source and Destination
else
Make the legal move between pegs Source and Destination
Make the legal move between pegs Source and Auxilary
endif
Make legal move between pegs Auxilary and Destination
}
end While
注:Source为A柱,Auxilary为辅助柱(B柱),Destination为目标柱(C柱)
翻译版
Algorithm:
While 当C柱上的盘子数小于总的盘子数的时候
do
{
if 盘子数是偶数:
A->B(合法移动)
A->C(合法移动)
else 盘子数是奇数:
A->C(合法移动)
A->B(合法移动)
endif
B->C(合法移动)
}
end While
合法移动:小的盘子移动到大的盘子上,请仔细体会
代码实现
/**
* 返回1:表示A->B 返回2:表示B->A 返回0:两个都是空的 其他;-1
* @param A
* @param B
* @return
*/
public static int legalMove(Stack<Integer> A,Stack<Integer> B){
int a,b;
try {
a = Integer.parseInt(A.peek().toString());
}
catch(EmptyStackException e){
a = 0;
}
try {
b = Integer.parseInt(B.peek().toString());
}
catch(EmptyStackException e){
b = 0;
}
//移动的两个柱子上都是空的
if(a==b) {
return 0;
}
if(a == 0)
{
//A空了 B ->A
A.push(B.pop());
return 2;
}
else if(b == 0)
{
//柱子B是空得 逆序 A->B
B.push(A.pop());
return 1;
}
if(a<b)
{
//A最上面的 比 B的小,A->B是合法的
B.push(A.pop());
return 1;
}
else if(a > b)
{
//B最上面的罗盘 比 A 的小,B->A是合法的
A.push(B.pop());
return 2;
}
return -1;
}
public static void main(String[] args) {
int stepNumber = 0;
int status = 0;
try {
Stack A = new Stack();
Stack B = new Stack();
Stack C = new Stack();
System.out.println("输入数量 : ");
BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(input.readLine());
if(n<=0)
{
System.out.println("输入有误!");
System.exit(1);
}
//元素进栈
for(int i=n; i>0; i--){
A.push(i);
}
//判断奇偶
int m = n%2;
do {
if(m==1)
{
//输入为奇数时
if((status = legalMove(A,C)) == 1){
System.out.println((++stepNumber) + ". A->C");
}
else if (status == 2){
System.out.println((++stepNumber) + ". C->A");
}
if((status = legalMove(A,B)) == 1){
System.out.println((++stepNumber) + ". A->B");
}
else if(status == 2){
System.out.println((++stepNumber) + ". B->A");
}
else{
break;
}
}
else
{
//偶数时
if((status = legalMove(A,B)) == 1){
System.out.println((++stepNumber) + ". A->B");
}
else if (status == 2){
System.out.println((++stepNumber) + ". B->A");
}
if((status = legalMove(A,C)) == 1){
System.out.println((++stepNumber) + ". A->C");
}
else if(status == 2){
System.out.println((++stepNumber) + ". C->A");
}
}
if((status = legalMove(B,C)) == 1){
System.out.println((++stepNumber) + ". B->C");
}
else if(status == 2){
System.out.println((++stepNumber) + ". C->B");
}
}while(C.size()!=n);
System.out.println("-----------------------");
}
catch (Exception e){
}
}
算法分析
- 时间复杂度: O((2^n - 1)/3),等同于 O(2^n)