为什么选择跳表
目前经常使用的平衡数据结构像B树,红黑树,AVL树等这些,想象一下,给你一张草稿纸,一只笔,一个编辑器,你能立即实现一颗红黑树,或者AVL树出来吗? 很难吧,这需要时间,要考虑很多细节,要参考一堆算法与数据结构之类的树,还要参考网上的代码,相当麻烦。
那么在这种情况下,我们就可以用跳表。
那么什么是跳表
跳表是一种随机化的数据结构,目前开源软件 Redis 和 LevelDB 都有用到它,它的效率和红黑树以及 AVL 树不相上下,但跳表的原理相当简单,只要你能熟练操作链表,就能轻松实现一SkipList。
有序表的搜索
考虑一个有序表:

从该有序表中搜索元素 < 23, 43, 59 > ,需要比较的次数分别为 < 2, 4, 6 >,总共比较的次数
为 2 + 4 + 6 = 12 次。因为链表不能用二分查找,二分查找是正对与数组的。那有没有优化的算法吗? 类似二叉搜索树,我们把一些节点提取出来,作为索引。得到如下结构:

这里我们把 < 14, 34, 50, 72 > 提取出来作为一级索引,这样搜索的时候就可以减少比较次数了。
我们还可以再从一级索引提取一些元素出来,作为二级索引,变成如下结构:
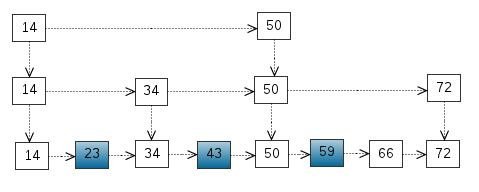
这里元素不多,体现不出优势,如果元素足够多,这种索引结构就能体现出优势来了。
这基本上就是跳表的核心思想,其实也是一种通过“空间来换取时间”的一个算法,通过在每个节点中增加了向前的指针,从而提升查找的效率。
下面的结构是就是跳表:
其中 -1 表示 INT_MIN, 链表的最小值,1 表示 INT_MAX,链表的最大值。
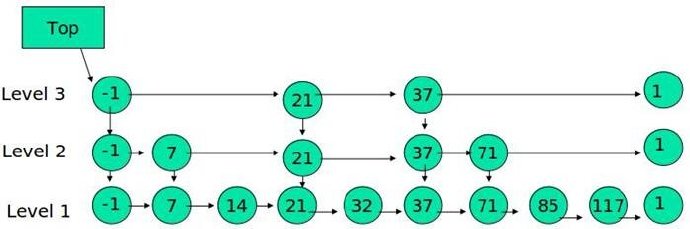
跳表具有如下性质:
(1) 由很多层结构组成
(2) 每一层都是一个有序的链表
(3) 最底层(Level 1)的链表包含所有元素
(4) 如果一个元素出现在 Level i 的链表中,则它在 Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
跳表的搜索

例如查找元素 117
(1) 比较 21, 比 21 大,往后面找
(2) 比较 37, 比 37大,比链表最大值小,从 37 的下面一层开始找
(3) 比较 71, 比 71 大,比链表最大值小,从 71 的下面一层开始找
(4) 比较 85, 比 85 大,从后面找
(5) 比较 117, 等于 117, 找到了节点。
java实现

import java.util.Random; public class SkipList { private static Node head; // 头结点 private static Node tail; // 尾结点 private static int level; // 层数 private static int size; // 节点个数 private static Random random; // 随机数来确定层数 public SkipList() { head = new Node(Integer.MIN_VALUE); // 头结点为最小值 tail = new Node(Integer.MAX_VALUE); // 尾结点为最大值 // 连起来 head.setRight(tail); tail.setLeft(head); level = 0; // 初始化层数为0 size = 0; // 初始化节点个数为0 random = new Random(); // new出random对象 } // 判断是否为空 public static boolean isEmpty() { if (size == 0) { return true; } return true; } // 查找到需要插入的前一个节点 public static Node findPrevNode(Integer data) { Node node = head; while (node != null) { // node的头结点不为尾结点并且node的值不大于data的时候,就一直往右走,否则循环结束 while (node.getRight() != tail && node.getRight().getValue() <= data) { node = node.getRight(); } // 如果当前节点有下节点,就继续往下走 if (node.getDown() != null) { node = node.getDown(); } else { // 否则返回当前节点 return node; } } return null; } // 查找节点 public static Node findNode(Integer data) { Node node = findPrevNode(data); if (node == null) { return null; } if (node.getValue() == data) { return node; } return null; } public static void add(Integer data) { // 找到前一个节点 Node prev = findPrevNode(data); if (prev == null) { return; } if (data == prev.getValue()) { System.out.println("插入重复"); return; } // 插入 Node addNode = new Node(data); addNode.setLeft(prev); addNode.setRight(prev.getRight()); prev.getRight().setLeft(addNode); prev.setRight(addNode); int high = 0;// 当前层数 while (random.nextDouble() < 0.5) { // 进行随机,是否需要往上层添加 if (high >= level) { // 如果当前层数超出了高度,就需要新建一层 Node node1 = new Node(Integer.MIN_VALUE); Node node2 = new Node(Integer.MAX_VALUE); node1.setRight(node2); node1.setDown(head); node2.setLeft(node1); node2.setDown(tail); head.setUp(node1); tail.setUp(node2); level++; head = node1; tail = node2; } // 找到最上一层 while (prev.getUp() == null) { prev = prev.getLeft(); } prev = prev.getUp(); Node node = new Node(data); node.setLeft(prev); node.setRight(prev.getRight()); node.setDown(addNode); prev.getRight().setLeft(node); prev.setRight(node); addNode.setUp(node); addNode = node; high++; // 高度+1 } size++; // 节点个数+1 } // 删除节点 public static boolean remove(Integer data) { Node node = findNode(data); if (node == null) { return false; } while (node != null) { node.getLeft().setRight(node.getRight()); node.getRight().setLeft(node.getLeft()); node = node.getUp(); } return true; } public static void print() { Node node; Node node1 = head; while (node1 != null) { int k = 0; node = node1; while (node != null) { System.out.print(node.getValue() + " "); k++; node = node.getRight(); } System.out.print(" "); System.out.print("(" + k + ")"); System.out.println(); node1 = node1.getDown(); } } public static void main(String[] args) { SkipList sl = new SkipList(); for (int i = 0; i < 30; i++) { // 随机数字进行测试 add(i); } print(); System.out.println("----------"); if (findNode(22) != null) { // 查找 System.out.println("OK"); } else {// 找不到 System.out.println("false"); } remove(0); // 删除 print(); } } // 定义节点 class Node { private Integer value; private Node up, down, left, right; public Node(Integer value) { this.value = value; } public Integer getValue() { return value; } public void setValue(Integer value) { this.value = value; } public Node getUp() { return up; } public void setUp(Node up) { this.up = up; } public Node getDown() { return down; } public void setDown(Node down) { this.down = down; } public Node getLeft() { return left; } public void setLeft(Node left) { this.left = left; } public Node getRight() { return right; } public void setRight(Node right) { this.right = right; } }
结果

