1. 图的定义
图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的;其中,点通常被成为"顶点(vertex)",而点与点之间的连线则被成为"边或弧"(edege)。通常记为,G=(V,E)。
2. 图的种类
根据边是否有方向,将图可以划分为:无向图和有向图。
2.1 无向图
(以下图片来自网络)
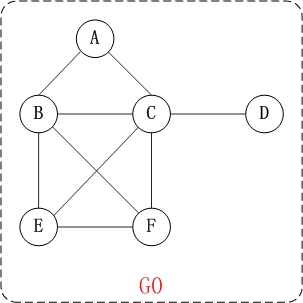
上面的图G0是无向图,无向图的所有的边都是不区分方向的。G0=(V1,{E1})。其中,
(01) V1={A,B,C,D,E,F}。 V1表示由"A,B,C,D,E,F"几个顶点组成的集合。
(02) E1={(A,B),(A,C),(B,C),(B,E),(B,F),(C,F), (C,D),(E,F),(C,E)}。 E1是由边(A,B),边(A,C)...等等组成的集合。其中,(A,C)表示由顶点A和顶点C连接成的边。
2.2 有向图
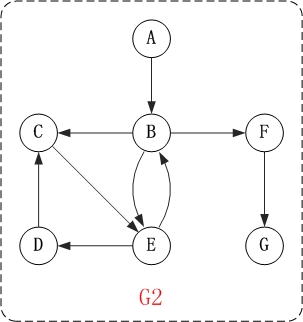
上面的图G2是有向图。和无向图不同,有向图的所有的边都是有方向的! G2=(V2,{A2})。其中:
(01) V2={A,C,B,F,D,E,G}。 V2表示由"A,B,C,D,E,F,G"几个顶点组成的集合。
(02) A2={<A,B>,<B,C>,<B,F>,<B,E>,<C,E>,<E,D>,<D,C>,<E,B>,<F,G>}。 E1是由矢量<A,B>,矢量<B,C>...等等组成的集合。其中,矢量<A,B)表示由"顶点A"指向"顶点C"的有向边。
3. 邻接点和度
3.1 邻接点
一条边上的两个顶点叫做邻接点。
例如,上面无向图G0中的顶点A和顶点C就是邻接点。
在有向图中,除了邻接点之外;还有"入边"和"出边"的概念。
顶点的入边,是指以该顶点为终点的边。而顶点的出边,则是指以该顶点为起点的边。
例如,上面有向图G2中的B和E是邻接点;<B,E>是B的出边,还是E的入边。
3.2 度
在无向图中,某个顶点的度是邻接到该顶点的边(或弧)的数目。
例如,上面无向图G0中顶点A的度是2。
在有向图中,度还有"入度"和"出度"之分。
某个顶点的入度,是指以该顶点为终点的边的数目。而顶点的出度,则是指以该顶点为起点的边的数目。
顶点的度=入度+出度。
例如,上面有向图G2中,顶点B的入度是2,出度是3;顶点B的度=2+3=5。
4. 路径和回路
- 路径:如果顶点(Vm)到顶点(Vn)之间存在一个顶点序列。则表示Vm到Vn是一条路径。
- 路径长度:路径中"边的数量"。
- 简单路径:若一条路径上顶点不重复出现,则是简单路径。
- 回路:若路径的第一个顶点和最后一个顶点相同,则是回路。
- 简单回路:第一个顶点和最后一个顶点相同,其它各顶点都不重复的回路则是简单回路。
5. 连通图和连通分量
- 连通图:对无向图而言,任意两个顶点之间都存在一条无向路径,则称该无向图为连通图。 对有向图而言,若图中任意两个顶点之间都存在一条有向路径,则称该有向图为强连通图。
- 连通分量:非连通图中的各个连通子图称为该图的连通分量。
6. 权
在学习"哈夫曼树"的时候,了解过"权"的概念。图中权的概念与此类似。
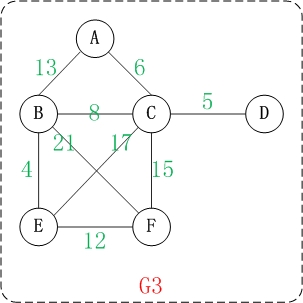
上面就是一个带权的图。
7. 图的存储结构
7.1. 邻接矩阵
邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。
假设图中顶点数为n,则邻接矩阵定义为:

下面通过示意图来进行解释。

图中的G1是无向图和它对应的邻接矩阵。
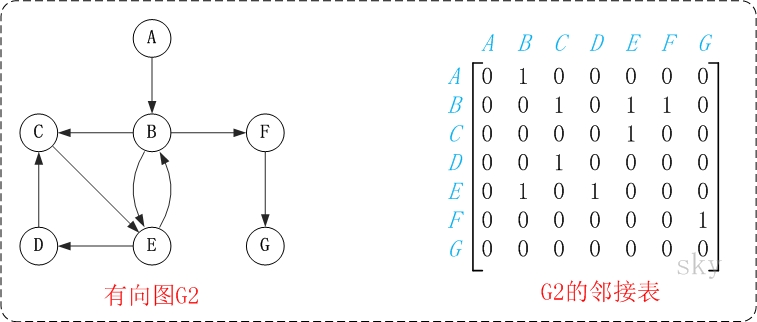
图中的G2是无向图和它对应的邻接矩阵。
通常采用两个数组来实现邻接矩阵:一个一维数组用来保存顶点信息,一个二维数组来用保存边的信息。
邻接矩阵的缺点就是比较耗费空间。
6.2. 邻接表
邻接表是图的一种链式存储表示方法。它是改进后的"邻接矩阵",它的缺点是不方便判断两个顶点之间是否有边,但是相对邻接矩阵来说更省空间。
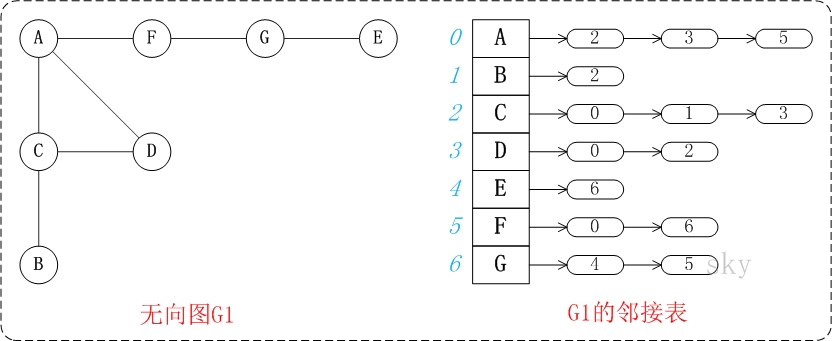
图中的G1是无向图和它对应的邻接矩阵。
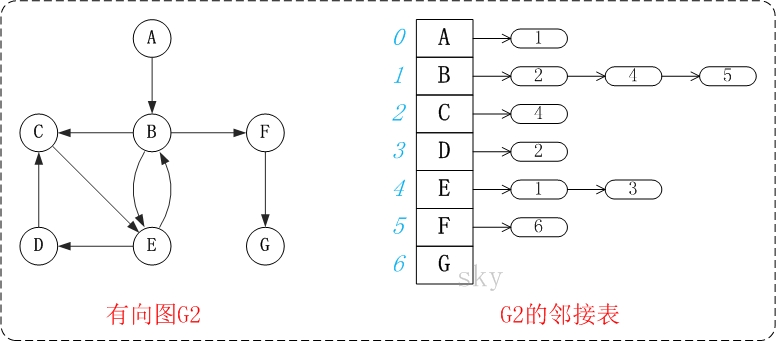
图中的G2是无向图和它对应的邻接矩阵。
8. Java代码实现求图的出度和入度
public class Graph { private int size; // 顶点数量 private int[] vertexs; // 顶点数组 private int[][] matrix; // 邻接矩阵 private static final int MAX_WEIGHT = 10000; public Graph(int size) { super(); this.size = size; vertexs = new int[size]; for (int i = 0; i < size; i++) { vertexs[i] = i; } matrix = new int[size][size]; } public int getSize() { return size; } public void setSize(int size) { this.size = size; } public int[] getVertexs() { return vertexs; } public void setVertexs(int[] vertexs) { this.vertexs = vertexs; } // 出度 public int outDegree(int index) { int degree = 0; for (int i = 0; i < matrix[index].length; i++) { int weight = matrix[index][i]; if (weight != 0 && weight != MAX_WEIGHT) { degree++; } } return degree; } // 入度 public int inDegree(int index) { int degree = 0; for (int i = 0; i < matrix.length; i++) { int weight = matrix[i][index]; if (weight != 0 && weight != MAX_WEIGHT) { degree++; } } return degree; } // 获取权值 public int getWeight(int v1, int v2) { int weight = matrix[v1][v2]; return weight == 0 ? 0 : (weight == MAX_WEIGHT ? -1 : weight); } // 获取最大出度 public int maxOutDegree() { int maxDegree = 0; for (int i = 0; i < matrix.length; i++) { int degree = outDegree(i); if (maxDegree < degree) { maxDegree = degree; } } return maxDegree; } // 获取最大入度 public int maxInDegree() { int maxDegree = 0; for (int i = 0; i < matrix[0].length; i++) { int degree = inDegree(i); if (maxDegree < degree) { maxDegree = degree; } } return maxDegree; } public static void main(String[] args) { Graph graph = new Graph(5); int[] a0 = new int[] { 0, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 6 }; int[] a1 = new int[] { 9, 0, 3, MAX_WEIGHT, MAX_WEIGHT }; int[] a2 = new int[] { 2, MAX_WEIGHT, 0, 5, MAX_WEIGHT }; int[] a3 = new int[] { 0, MAX_WEIGHT, MAX_WEIGHT, 0, 1 }; int[] a4 = new int[] { 0, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 }; graph.matrix[0] = a0; graph.matrix[1] = a1; graph.matrix[2] = a2; graph.matrix[3] = a3; graph.matrix[4] = a4; System.out.println("v0的出度:" + graph.outDegree(0)); System.out.println("v0的入度:" + graph.inDegree(0)); System.out.println("v0到v1的权值:" + graph.getWeight(0, 1)); System.out.println("v1到v0的权值:" + graph.getWeight(1, 0)); System.out.println("最大出度:" + graph.maxOutDegree()); System.out.println("最大入度:" + graph.maxInDegree()); } }