回溯法
一种选优搜索法,又称试探法。利用试探性的方法,在包含问题所有解的解空间树中,将可能的结果搜索一遍,从而获得满足条件的解。搜索过程采用深度遍历策略,并随时判定结点是否满足条件要求,满足要求就继续向下搜索,若不满足要求则回溯到上一层,这种解决问题的方法称为回溯法。
回溯法解求解问题步骤
- 针对给定问题,定义问题的解空间树;
- 确定易于搜索的解空间结构;
- 以深度优先方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索;
- 用回溯法求解问题,重点是设计问题的解空间树,其解题过程则是深度遍历解空间树的过程。
解空间树
是依据待求解问题的特性,用树结构表示问题的解结构、用叶子表示问题所有可能的解的一棵树。
解空间树的形成过程
我们可以把求解问题的过程当作一系列的决定来考虑,回溯法对每一个决定都系统地分析所有可能的结果。而每一次决定即为解空间树中的一个分支结点,各种可能的结果便形成了各棵不同的子树,问题最终所有可能的解将展现在所有的叶子上。这便是解空间树的形成过程。
对解空间树的遍历可搜索到问题所有可能的解,因此,可获得满足要求的全部解,也可通过对所有解的比较选择获得最优解。
由于空间问题,下面给出一个三皇后问题的解空间树(3皇后问题无解),树中第i层的结点决定第i行皇后的摆放位置,均有三种不同的选择,便形成了三个孩子结点,但其中不包括不符合要求的布局。N皇后问题解空间树与三皇后问题解空间树类似。
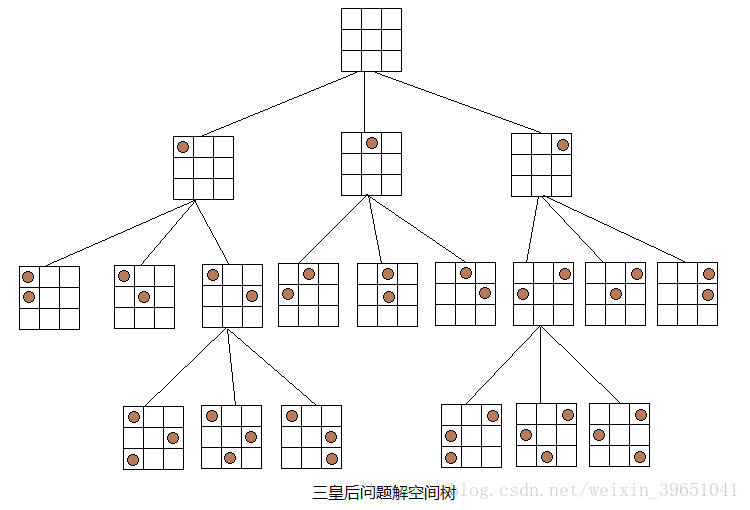
求解N皇后问题的回溯法
N皇后问题要求求解在N*N的棋盘上放置N个皇后,并使各皇后彼此不受攻击的所有可能的棋盘布局。皇后彼此不受攻击的约束条件是:任何两个皇后均不能在棋盘上同一行、同一列或者同一对角线上出现。
由于N皇后问题不允许两个皇后在同一行,所以,可用一维数组X表示N皇后问题的解,X[i]表示第i行的皇后所在的列号。例如一个满足要求的四皇后棋盘布局如下图所示,其结果X数组的值为:[2, 4, 1, 3]。

由上述X数组求解N皇后问题,保障了任意两个皇后不在同一行上,而判定皇后彼此不受攻击的其他条件,可以描述如下:
(1)X[i] = X[s],则第i行与第s行皇后在同一列上。
(2)如果第i行的皇后在第j列,第s行皇后在第t列,即X[i] = j和X[s] = t,则只要i-j = s-t或者i+j = s+t,说明两个皇后在同一对角线上。
对两个等式进行变换后,得到结论:只要|i-s| = |j-t|(即i-s = X[i]-X[s]),则皇后在同一对角线上。
解N皇后问题需要遍历解空间树,遍历中要随时判定当前结点棋盘布局是否符合要求,符合要求则继续向下遍历,直至判断得到一个满足约束条件的叶子结点,从而获得一个满足要求的棋盘布局;不符合要求的结点将被舍弃(称之为剪枝),并回溯到上一层的结点继续遍历。当整棵树遍历结束时,已获得所有满足要求的棋盘布局。
八皇后问题java实现:
public class Queen { public static int num = 0; // 方案数 public static final int MAXQUEEN = 8; // 皇后数 public static int[] cols = new int[MAXQUEEN]; // 定义数组,表示MAXQUEEN列棋子中皇后摆放位置 /* * @param n:填第n列的皇后 */ public void getCount(int n) { boolean[] rows = new boolean[MAXQUEEN]; for (int m = 0; m < n; m++) { rows[cols[m]] = true; int d = n - m; // 正斜方向 if (cols[m] - d >= 0) { rows[cols[m] - d] = true; } // 反斜方向 if (cols[m] + d <= (MAXQUEEN - 1)) { rows[cols[m] + d] = true; } } for (int i = 0; i < MAXQUEEN; i++) { if (rows[i]) { // 不能放 continue; } cols[n] = i; // 下面仍然有合法位置 if (n < MAXQUEEN - 1) { getCount(n + 1); } else { // 找到完整的一套方案 num++; printQueen(); } } } private void printQueen() { System.out.println("第" + num + "种方案"); for (int i = 0; i < MAXQUEEN; i++) { for (int j = 0; j < MAXQUEEN; j++) { if (i == cols[j]) { System.out.print("0 "); } else { System.out.print("+ "); } } System.out.println(); } } public static void main(String[] args) { Queen queen = new Queen(); queen.getCount(0); } }