定义
2-3树是平衡的3路查找树,其中2(2-node)是指拥有两个分支的节点,3(3-node)是指拥有三个分支的节点。B-树是一种平衡的多路查找树,2-3树属于b-树,其也同样具有B-树的性质,如m阶B-树,节点至多有m个分支、m-1个关键字;内部节点的分支数至少为m/2取上限;所有叶节点都出现在同一层次上,并且不带任何信息(这是由构造树的逻辑决定的,实际上指向这些节点的引用为null)。
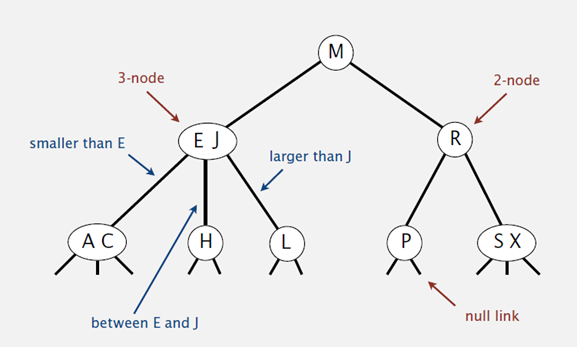
2-3查找树的定义如下:
1 对于2节点,该节点保存一个key及对应value,以及两个指向左右节点的节点,左节点也是一个2-3节点,所有的值都比key有效,有节点也是一个2-3节点,所有的值比key要大。
2. 对于3节点,该节点保存两个key及对应value,以及三个指向左中右的节点。左节点也是一个2-3节点,所有的值均比两个key中的最小的key还要小;中间节点也是一个2-3节点,中间节点的key值在两个跟节点key值之间;右节点也是一个2-3节点,节点的所有key值比两个key中的最大的key还要大。
插入
永远都是在叶节点处插入新节点,当3-node变为4-node时,需要拆分节点,此时树高就有可能增加。

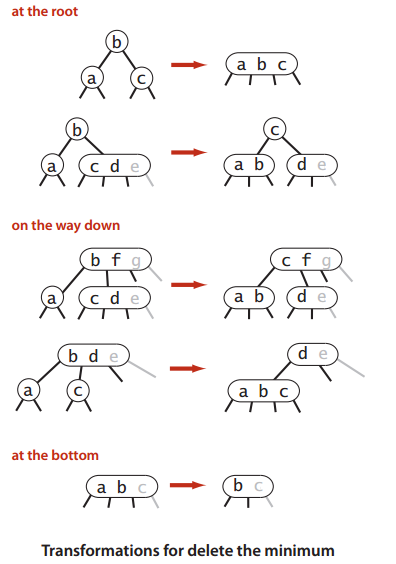
删除
删除节点比插入节点麻烦一些,先来看删除底部节点,在搜索过程中就需要对节点做相应的变化,以保证搜索路径上的都是3-node或临时的4-node,在删除当前节点T时,T一定是3-node或4-node,就可以安全删除了,删除之后树的变化规则与插入一致。删除其他节点可以转化为删除底部节点,只需要将删除元素与底部节点元素交换即可。
总结
2-3树作为一种平衡查找树,查询效率比普通的二叉排序树要稳定许多,其操作逻辑也非常清晰。2-3树可以采用红黑树实现,使用二叉树结构从逻辑上模拟了2-3树,在插入删除节点时,又具有二叉平衡树的便利。