通用树的理论知识
一、树的定义
由一个或多个(n>=0)节点组成的有限集合T,有且仅有一个节点称为根(root),当n>1时,其7余的节点为m(m>=0)个互不相交的有限集合T1,T2,...,Tm。每个集合本身又是棵树,称其为根的子树。
注意:空树也是树,树具有递归性。
二、树的相关术语
1. 根:根节点(没有前驱)。
2. 叶子:终端节点(没有后继)。
3. 森林:m棵不相交树的集合。
4. 有序树:节点从上至下、从左至右有有序,不能互换
5. 双亲:节点的直接前驱。
6. 孩子:节点的直接后继。
7. 兄弟:同一双亲下的同层节点。
8. 堂兄弟:不同双亲的同层节点。
9. 祖先:从根节点到该节点所经分支的所有节点。
10. 子孙:从该节点的下层子树的任一节点。
11. 节点:树的数据元素。
12. 节点的度:直接后继的个数。
13. 节点的层次:从根到该节点的层数,根节点所在的层数为1。
14. 终端节点:度数为0的节点,就是叶子。
15. 分支节点:树根除外的节点。
16. 树的度:所有节点度中的最大值。
17. 树的深度:所有节点中最大的层数。
三、树的表示法
1. 广义表示法:(A(B(E(K,L),F),C(G),D(H(M),I,J)))
2. 左孩子右兄弟表示法:每个节点有两个指针域,一个指向其长子,另一个指向其兄弟。
3.双亲表示法:让每个结点记住其父结点的位置。存储数据元素的结点由两部分组成:存储数据元素值的数据字段,以及存储父结点位置的字段。
四、树的物理存储结构
顺序储存、链式存储。
五、树的运算
普通的树如果不能转化为二叉树,则运算很难实现。二叉树的运算有插入、删除、修改、查找、排序等,这些操作必须建立在对树节点遍历之上。
六、普通树转二叉树(左儿子,右兄弟)
- 将树的根节点直接作为二叉树的根节点。
- 将树的根节点的第一个子节点作为根节点的左儿子,若该子节点存在兄弟节点,则将该子节点的第一个兄弟节点(方向从左往右)作为该子节点的右儿子。
- 将树中的剩余节点按照上一步的方式,依序添加到二叉树中,直到树中所有的节点都在二叉树中。
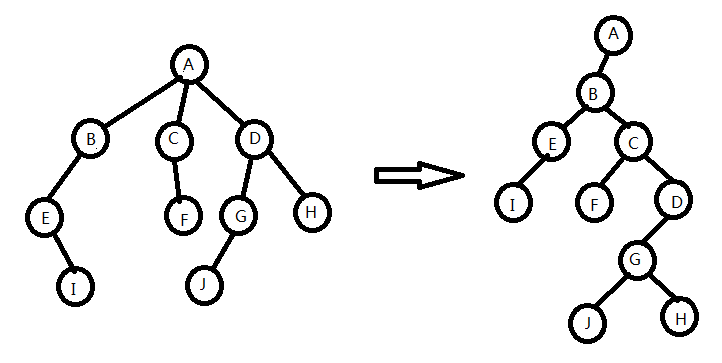
其实就是每个点的左儿子是它的第一个儿子,右儿子是它从左往右数的第一个兄弟。
二叉树的补充理论知识
一、二叉树的定义
n(n>=0)个节点的有限集合,由一个根节点以及两棵互不相交的左子树、右子树组成。
二、二叉树逻辑结构
一对二(1:2)
三、二叉树基本特征
每个节点最多只有两棵子树,不存在度大于2的节点,左子树和右子树次序不能颠倒。
四、二叉树的五种基本形态
(1)空二叉树;
(2)只有一个根结点;
(3)根结点只有左子树;
(4)根结点只有右子树(完全二叉树不具备这种形态);
(5)根结点既有左子树又有右子树。
五、二叉树的性质
1. 二叉树的第i层上至多有2的i-1次方个节点(i>0)。
2. 深度为k的二叉树至多有2的k次方-1个节点(k>0)。
3. 二叉树,n0 = n2 + 1(n0表示叶子数,n2表示度为2的节点数)
4. 满二叉树:每层都充满了节点
5. 完全二叉树:满二叉树中,编号1~n,满足至上而下、从左至右与节点一一对应。完全二叉树最后一层叶子可以不满,但必须集中在左边。
6. 完全二叉树,具有n个节点的深度必为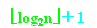
7. 完全二叉树,若编号为i的节点,其左孩子编号必为2i,其右孩子编号必为2i+1。
8.满二叉树的特点:
(1)叶子只能出现在最下一层。出现在其他层就不可能达到平衡。
(2)非叶子结点的度一定是2。
(3)在同样深度的二叉树中,满二叉树的结点个数最多,叶子树最多。
9.完全二叉树的特点:
(1)叶子结点只能出现在最下两层。
(2)最下层的叶子一定集中在左部连续位置
(3)倒数二层,若有叶子结点,一定都在右部连续位置。
(4)如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况。
(5)同样结点数的二叉树,完全二叉树的深度最小。
注意:满二叉树一定是棵完全二叉树,但完全二叉树不一定是满的。
10.题目:深度为9的二叉树中至少有多少个节点,答:9个节点(注意:这里是二叉树而不是完全二叉树)
11.为什么要研究满二叉树和完全二叉树这两种特殊形式,答:只有这两种形式可以实现顺序存储。
12.完全二叉树,具有1000个节点,则叶子节点有多少个,度为2的节点有多少个,有多少个节点只有非空左子树,有多少个节点只有非空右子树。答:总层数: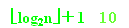
,完全二叉树前9层总节点数为511个,末层叶子数为489个,叶子数为奇数说明有一个非空左子树,完全二叉树不可能出现只有右子树
13.树执行查找、删除、插入的时间复杂度都是O(logN)
五、二叉树的顺序存储
按二叉树的节点“自上而下,从左至右”编号,用一组连续的存储单元存储。
规律:下标为i的双亲,其左孩子下标必定为2i,其右孩子下标必定为2i+1,例如[2]、[4]、[5]
若不是完全二叉树就转化为完全二叉树,方法简单,就是将各层空缺统统补上节点,内容为空,缺点:浪费空间,插入删除不方便。
六、二叉树的链式存储结构
用二叉链表即可方便表示,从根节点开始存储,相应的,访问树中的节点也只能从根节点开始。
如果需要倒插某节点的双亲,可以再增加一个双亲域(直接前趋)指针,将二叉链表变成三叉链表。
七、遍历二叉树
1. 遍历又称周游。
2. 遍历的用途:是树结构插入、删除、修改、查找、排序运算的前提。
3. 遍历方法:先左后右
八、遍历方案(下一篇博文会具体实现树的遍历)
先(根)序遍历,中(根)序遍历、后(根)序遍历,层序遍历。