一、梯度下降
最简单的梯度下降算法——固定学习率
x -= grad*lr
步长的选择:
步长太小对局部极小值的逼近慢,训练时间长
步长太大,模型容易震荡,结果不收敛
二、Adam法梯度下降
动量法梯度下降:(当前更新量+之前值 )的平滑
冲量的“惯性”
pre_grad = pre_grad*discount + grad*lr
x -= pre_grad
目的:积累梯度方向(分量)会逐步增强,帮助目标穿越“狭窄山谷”形状的优化曲面;从而加快了训练速度
比如Nesterov
自适应法:自适应确定更新量,使得更新量更加均衡,不随梯度显著变化;即参数的优化更加均衡
“启动快”,善于处理“爬坡”
x -= lr * f(grad)
比如Adagrad
Adam法融合以上两种思路的优点
三、局部最优与全局最优
The Loss Surfaces of Multilayer Networks
Deep Learning without Poor Local Minima
以上两篇论文结论:随着模型复杂度上升,局部最优点的目标函数值和全局最优点的函数值的差距在不断缩小。
这样即使模型参数收敛到一个局部最优值上,模型表现依然很好。
对上述结论一种简化的理解(不定方程理论):如果把神经网络抽象成一个线性变换的过程,那么这个问题相当于求解一个参数数量多于方程数量的方程组。这样的问题是很可能有多于一个解的。
如果模型变得复杂,相当于参数数量进一步增加,那么解的数量也会变得更多。所以在深层网络中存在参数不同但结果相近的现象是很有可能的。
优化中的一对矛盾:
a) 模型复杂度:随着参数数量增大和模型深度加深,求解模型的全局最优值变得越来越困难。
b) 模型优化满意度:模型复杂度越高,局部最优点效果越逼近全局最优点。
四、正则化
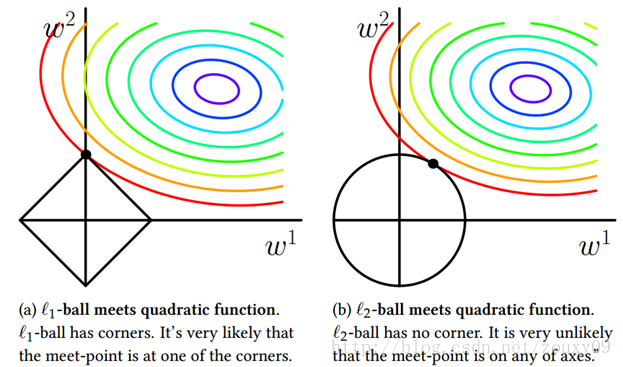
左为L1范数,右为L2范数
可见L1正则约束下,目标函数最优值更容易出现在坐标轴上。
优化目标公式: Obj(w) = Loss(w) + L1/L2(w)
L1即参数平均值,此正则约束下,最优参数具有稀疏性;相应参数规模会减小L
求解:
L1正则在原点处不可导,求解L1正则使用的是“次梯度下降算法”
L2正则是求参数w的平方值,用于防止过拟合。一般采用L2正则。
五、深层模型泛化
深层模型的复杂度很难用传统机器学习中的量化指标(比如VC维)来衡量。
通过过拟合来提高深层模型的泛化能力:
1、前提:模型的输入空间在某个领域内具备泛化能力。
2、手段:
a)补充足够多的数据,覆盖更大的样本输入空间
b)让局部泛化的范围变大——比如L2限制了参数大小,可以让模型在局部表现得比较平滑,从而起到一些效果;Batch Norm也限制了模型,所以也能起到一些效果。