题目链接:bzoj4237
loj2880
考虑(cdq)分治,按(x)坐标排序,于是问题变成统计左下角在([l,mid]),右上角在([mid+1,r])的矩形数量
我们先考虑固定左下角,来看一下右上角是如何变化的
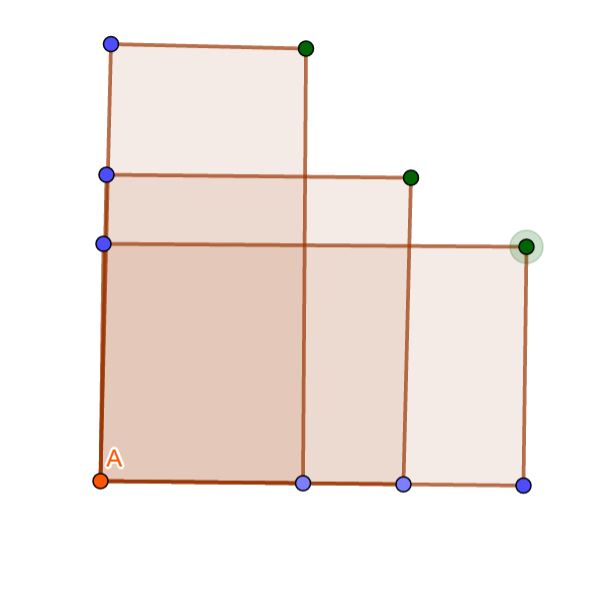
当我们固定左下角A(橙色点)的时候,我们注意到右上角的点的(x)坐标单调递减,(y)单调递增
我们再考虑左下角发生变化的情况
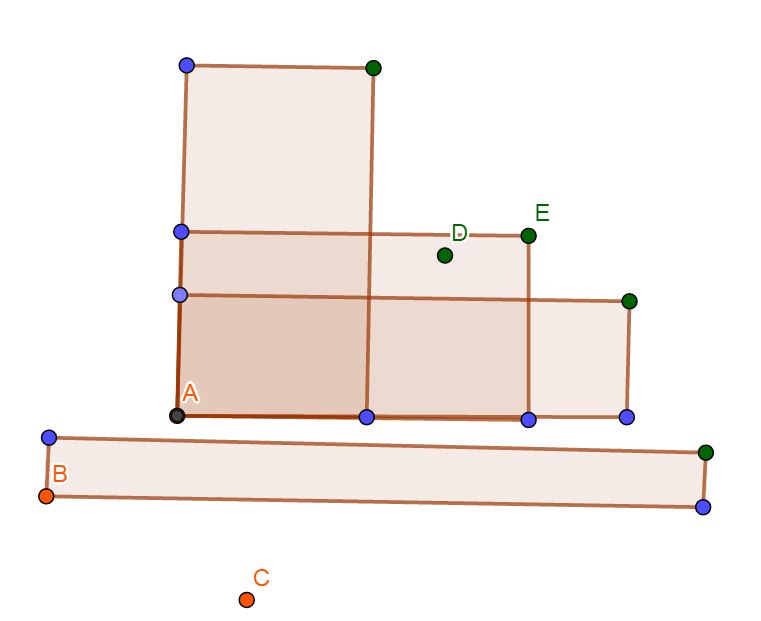
此时左边有三个点(A,B,C),右边有四个绿色的点(不含点(D)),(A)可以和右边上方的三个点产生贡献,(B)只能和右边最下方的一个点产生贡献,(C)可以和右边的所有点产生贡献。说明对于左边的两个点(P)和(Q),如果满足(P_x<Q_x)且(P_y>Q_y),那么可以与(P)产生贡献的点也可以与(Q)产生贡献
再来看一下上图,假设多了一个点(D),注意到点(D)在点(E)的左下方,这使得点(E)一定不会产生贡献
同理,对于左边的点,只有当前的点的左上方有原来的点的情况下,这个点和右边的点的组合才会产生影响
于是解法就比较清晰了
对于左边的点和右边的点分别维护一个单调栈,左边的点的(x)单调递减,右边的点的(x)单调递增,每次将(y)从小到大进行排序依次加点,维护单调栈的同时二分(y)统计右边有多少个合法点
#include<iostream>
#include<string.h>
#include<string>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
using namespace std;
#define lowbit(x) (x)&(-x)
#define fir first
#define sec second
#define rep(i,a,b) for (register int i=a;i<=b;i++)
#define per(i,a,b) for (register int i=a;i>=b;i--)
#define maxd 1000000007
typedef long long ll;
const int N=100000;
const double pi=acos(-1.0);
struct node{
int x,y;
}point[200500];
bool operator<(const node &p,const node &q)
{
return p.y>q.y;
}
bool cmp(node p,node q)
{
return p.x<q.x;
}
int n,st1[200200],st2[200200];
ll ans=0;
int read()
{
int x=0,f=1;char ch=getchar();
while ((ch<'0') || (ch>'9')) {if (ch=='-') f=-1;ch=getchar();}
while ((ch>='0') && (ch<='9')) {x=x*10+(ch-'0');ch=getchar();}
return x*f;
}
void cdq(int l,int r)
{
if (l==r) return;
int mid=(l+r)>>1;
cdq(l,mid);cdq(mid+1,r);
sort(point+l,point+mid+1);
sort(point+mid+1,point+r+1);
int tp1=0,tp2=0,pos2=mid+1;
rep(i,l,mid)
{
while ((pos2<=r) && (point[pos2].y>point[i].y))
{
while ((tp2) && (point[st2[tp2]].x>point[pos2].x)) tp2--;
st2[++tp2]=pos2;pos2++;
}
while ((tp1) && (point[st1[tp1]].x<point[i].x)) tp1--;
st1[++tp1]=i;
if (tp1==1) ans+=tp2;
else
{
int l=1,r=tp2,now=tp2+1,val=point[st1[tp1-1]].y;
while (l<=r)
{
int mid=(l+r)>>1;
if (point[st2[mid]].y>val) l=mid+1;
else {r=mid-1;now=mid;}
}
ans+=(tp2-now+1);
}
}
}
int main()
{
n=read();
rep(i,1,n)
{
point[i].x=read();point[i].y=read();
}
sort(point+1,point+1+n,cmp);
cdq(1,n);
printf("%lld",ans);
return 0;
}