【图论】有向无环图的拓扑排序

1. 引言

有向无环图（Directed Acyclic Graph, DAG）是有向图的一种，字面意思的理解就是图中没有环。常常被用来表示事件之间的驱动依赖关系，管理任务之间的调度。拓扑排序是对DAG的顶点进行排序，使得对每一条有向边(u, v)，均有u（在排序记录中）比v先出现。亦可理解为对某点v而言，只有当v的所有源点均出现了，v才能出现。

下图给出有向无环图的拓扑排序：

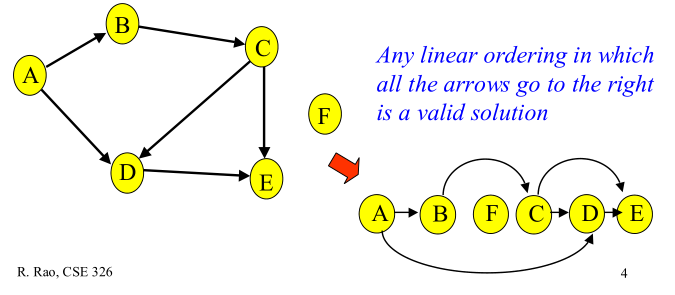
下图给出的顶点排序不是拓扑排序，因为顶点D的邻接点E比其先出现：

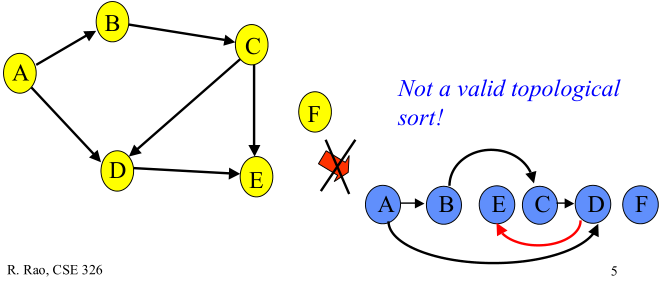
2. 算法原理与实现

拓扑排序的实现算法有两种：入度表、DFS，其时间复杂度均为(O(V+E))。

入度表

对于DAG的拓扑排序，显而易见的办法：

• 找出图中0入度的顶点；
• 依次在图中删除这些顶点，删除后再找出0入度的顶点；
• 然后再删除……再找出……
• 直至删除所有顶点，即完成拓扑排序

为了保存0入度的顶点，我们采用数据结构栈（亦可用队列）；算法的可视化可参看这里。

图用邻接表（adjacency list）表示，用数组inDegreeArray[]记录结点的入度变化情况。C实现：

// get in-degree array
int *getInDegree(Graph *g) {
    int *inDegreeArray = (int *) malloc(g->V * sizeof(int));
    memset(inDegreeArray, 0, g->V * sizeof(int));
    int i;
    AdjListNode *pCrawl;
    for(i = 0; i < g->V; i++) {
        pCrawl = g->array[i].head;
        while(pCrawl) {
            inDegreeArray[pCrawl->dest]++;
            pCrawl = pCrawl->next;
        }
    }
    return inDegreeArray;
}

// topological sort function
void topologicalSort(Graph *g) {
    int *inDegreeArray = getInDegree(g);
    Stack *zeroInDegree = initStack();
    int i;
    for(i = 0; i < g->V; i++) {
        if(inDegreeArray[i] == 0)
            push(i, zeroInDegree);
    }

    printf("topological sorted order
");
    AdjListNode *pCrawl;
    while(!isEmpty(zeroInDegree)) {
        i = pop(zeroInDegree);
        printf("vertex %d
", i);

        pCrawl = g->array[i].head;
        while(pCrawl) {
            inDegreeArray[pCrawl->dest]--;
            if(inDegreeArray[pCrawl->dest] == 0)
                push(pCrawl->dest, zeroInDegree);
            pCrawl = pCrawl->next;
        }
    }
}

时间复杂度：得到inDegreeArray[]数组的复杂度为(O(V+E))；顶点进栈出栈，其复杂度为(O(V))；删除顶点后将邻接点的入度减1，其复杂度为(O(E))；整个算法的复杂度为(O(V+E))。

DFS

在DFS中，依次打印所遍历到的顶点；而在拓扑排序时，顶点必须比其邻接点先出现。在下图中，顶点5比顶点0先出现，顶点4比顶点1先出现。

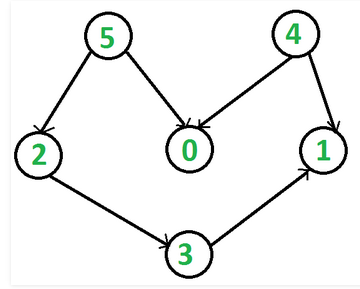
在DFS实现拓扑排序时，用栈来保存拓扑排序的顶点序列；并且保证在某顶点入栈前，其所有邻接点已入栈。DFS版拓扑排序的可视化参看这里。

C实现：

/* recursive DFS function to traverse the graph,
* the graph is represented by adjacency list
*/
void dfs(int u, Graph *g, int *visit, Stack *s) {
   visit[u] = 1;
   AdjListNode *pCrawl = g->array[u].head;
   while(pCrawl) {
       if(!visit[pCrawl->dest])
           dfs(pCrawl->dest, g, visit, s);
       pCrawl = pCrawl->next;
   }
   push(u, s);
}

// the topological sort function
void topologicalSort(Graph *g) {
   int *visit = (int *) malloc(g->V * sizeof(int));
   memset(visit, 0, g->V * sizeof(int));
   Stack *s = initStack();
   int i;
   for(i = 0; i < g->V; i++) {
       if(!visit[i]) dfs(i, g, visit, s);
   }

   // the order of stack element is the sorted order
   while(!isEmpty(s)) {
       printf("vertex %d
", pop(s));
   }
}

时间复杂度：应与DFS相同，为(O(V+E))。

---

完整代码在Github。

3. 参考资料

[1] R. Rao, Lecture 20: Topo-Sort and Dijkstra’s Greedy Idea.
[2] GeeksforGeeks, Topological Sorting.
[3] GeeksforGeeks, Graph and its representations.