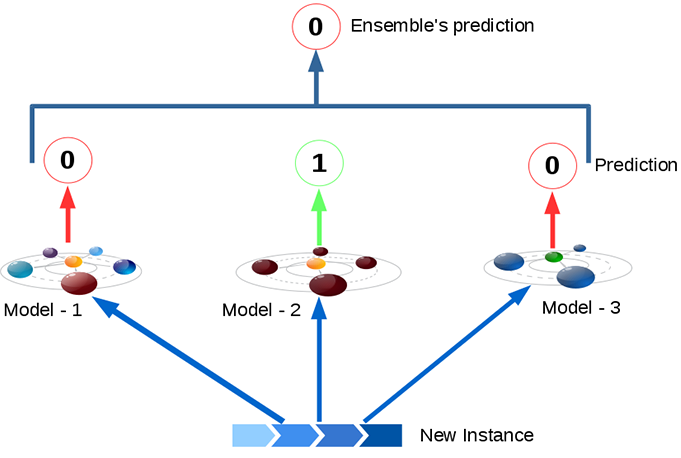
Hard voting is where a model is selected from an ensemble to make the final prediction by a simple majority vote for accuracy.
Soft Voting can only be done when all your classifiers can calculate probabilities for the outcomes. Soft voting arrives at the best result by averaging out the probabilities calculated by individual algorithms.
---------------------------
Understanding different voting schemes
Two different voting schemes are common among voting classifiers:
- In hard voting (also known as majority voting), every individual classifier votes for a class, and the majority wins. In statistical terms, the predicted target label of the ensemble is the mode of the distribution of individually predicted labels.
- In soft voting, every individual classifier provides a probability value that a specific data point belongs to a particular target class. The predictions are weighted by the classifier's importance and summed up. Then the target label with the greatest sum of weighted probabilities wins the vote.
For example, let's assume we have three different classifiers in the ensemble that perform a binary ...
---------------------------
In classification, a hard voting ensemble involves summing the votes for crisp class labels from other models and predicting the class with the most votes. A soft voting ensemble involves summing the predicted probabilities for class labels and predicting the class label with the largest sum probability.
---------------------------

---------------------------
Let's take a simple example to illustrate how both approaches work.
Imagine that you have 3 classifiers (1, 2, 3) and two classes (A, B), and after training you are predicting the class of a single point.
Hard voting
Predictions:
Classifier 1 predicts class A
Classifier 2 predicts class B
Classifier 3 predicts class B
2/3 classifiers predict class B, so class B is the ensemble decision.
Soft voting
Predictions
(This is identical to the earlier example, but now expressed in terms of probabilities. Values shown only for class A here because the problem is binary):
Classifier 1 predicts class A with probability 99%
Classifier 2 predicts class A with probability 49%
Classifier 3 predicts class A with probability 49%
The average probability of belonging to class A across the classifiers is (99 + 49 + 49) / 3 = 65.67%. Therefore, class A is the ensemble decision.
So you can see that in the same case, soft and hard voting can lead to different decisions. Soft voting can improve on hard voting because it takes into account more information; it uses each classifier's uncertainty in the final decision. The high uncertainty in classifiers 2 and 3 here essentially meant that the final ensemble decision relied strongly on classifier 1.
This is an extreme example, but it's not uncommon for this uncertainty to alter the final decision.
-------------------
Hard Voting Classifier : Aggregate predections of each classifier and predict the class that gets most votes. This is called as “majority – voting” or “Hard – voting” classifier.
Soft Voting Classifier : In an ensemble model, all classifiers (algorithms) are able to estimate class probabilities (i.e., they all have predict_proba() method), then we can specify Scikit-Learn to predict the class with the highest probability, averaged over all the individual classifiers.
| Modle Name | Class – 1 Probability | Class – 0 Probability |
|---|---|---|
| Model – 1 | 0.49 | 0.51 |
| Model – 2 | 0.99 | 0.01 |
| Model – 3 | 0.49 | 0.51 |
| Averages | 0.66 | 0.34 |
REF:
https://towardsdatascience.com/ensemble-learning-in-machine-learning-getting-started-4ed85eb38e00
https://machinelearningmastery.com/voting-ensembles-with-python/
https://stats.stackexchange.com/questions/349540/hard-voting-soft-voting-in-ensemble-based-methods
https://www.datajango.com/heterogeneous-ensemble-learning-hard-voting-soft-voting/