第一题,签到,参照一个人,考虑另外一个人的上限和下限

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 int main(){ 5 int tt,n,x,y,num; 6 string s,t; 7 cin>>tt; 8 while(tt--){ 9 num=0; 10 cin>>n>>x>>y; 11 cin>>s>>t; 12 for(int i=0;i<n;i++){ 13 if(s[i]!=t[i]) num++; 14 } 15 if(x<y) swap(x,y); 16 int t2=n-num;//xiangdeng 17 if(abs(x-y)>num||y<t2-n+x||x<t2-n+y||y>2*n-num-x||x>2*n-num-y) cout<<"Lying "; 18 else cout<<"Not lying "; 19 } 20 }
第三题,预处理一下后缀最大值,直接贪心,最后的细节处理很重要,将n之前的最值和之后的最值分别处理

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 #define inf 0x3f3f3f3f 5 const int mod=1e9+7; 6 int a[300005],b[300005]; 7 int mx[300005]; 8 int anss[300005]; 9 int main(){ 10 int n; 11 while(scanf("%d",&n)!=EOF){ 12 memset(mx,0,sizeof mx); 13 for(int i=1;i<=n;i++) scanf("%d",a+i); 14 for(int i=1;i<=n;i++) scanf("%d",b+i); 15 mx[n+1]=-inf; 16 for(int i=n;i>=1;i--){ 17 mx[i]=max(a[i]-i,mx[i+1]);//预处理后缀最大值 18 } 19 sort(b+1,b+n+1); 20 int ans=0,t=-inf; 21 for(int i=1;i<=n;i++){ 22 mx[b[i]]=max(mx[b[i]],t); 23 ans=(ans+mx[b[i]])%mod; 24 t=max(mx[b[i]]-n-i,t); 25 } 26 printf("%d ",ans); 27 } 28 return 0; 29 }
hdu6048 解题关键:将此题转化为求原序列逆序对的奇偶性的问题,然后找规律即可。(貌似题意有问题?2.Picking out the 1st ,the P+1 th ,the 2*P+1 th,......the n*P+1 th jigsaws and put them back to the blank area in the board one by one from the top row to the bottom row,from the left column to the right column.)至今没搞懂 为什么是先从左向右排,然后自上而下。看样例才明白的
逆序对的求法:某位置在之后(前)造成的逆序对累加(最直观)
官方题解说的比较详细,贴一下:
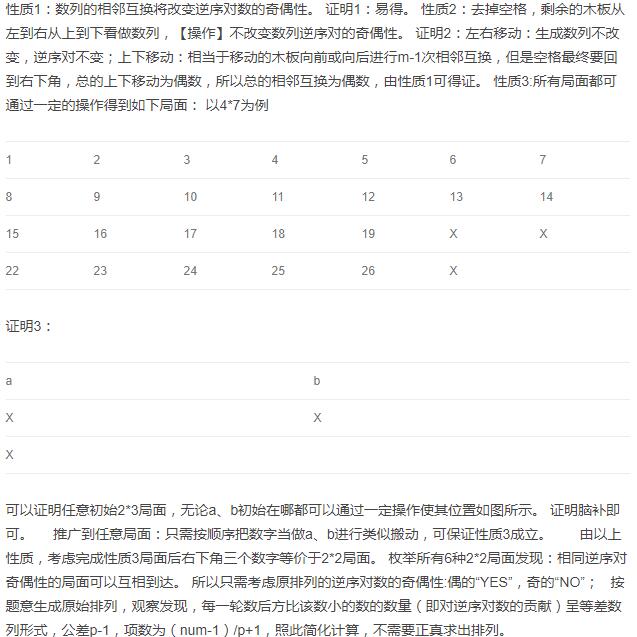

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 int main(){ 5 int t,n,m,p,ans; 6 cin>>t; 7 while(t--){ 8 ans=0; 9 cin>>n>>m>>p; 10 int num=n*m-1; 11 while(num>p){ 12 int temp=(num-1)/p+1; 13 ans+=(temp-1)*temp/2*(p-1); 14 num-=temp; 15 } 16 if(ans&1) cout<<"NO "; 17 else cout<<"YES "; 18 } 19 return 0; 20 }
1009 莫比乌斯反演的应用,容斥亦可做,注意优化,关键思路:总的组合数-gcd=1的情况
超时做法:

1 #include<bits/stdc++.h> 2 #define inf 0x3f3f3f3f 3 using namespace std; 4 typedef long long ll; 5 const int mod=1e9+7; 6 int mu[100005],a[100005]; 7 int mm=100000; 8 void sieve(){ 9 mu[1]=1; 10 for(int i=1;i<=mm;i++){ 11 for(int j=2*i;j<=mm;j+=i){ 12 mu[j]-=mu[i]; 13 } 14 } 15 } 16 17 ll mod_pow(ll x,ll n,ll p){ 18 ll res=1; 19 while(n){ 20 if(n&1) res=res*x%p; 21 x=x*x%p; 22 n>>=1; 23 } 24 return res; 25 } 26 27 int main(){ 28 sieve(); 29 ll t,n,mi,ans; 30 //ios::sync_with_stdio(0); 31 scanf("%lld",&t); 32 for(int k=1;k<=t;k++){ 33 scanf("%lld",&n); 34 ans=0; 35 mi=inf; 36 for(int i=0;i<n;i++) {cin>>a[i];mi=min(mi,(ll)a[i]);} 37 for(int i=2;i<=mi;i++){ 38 ll temp=1; 39 for(int j=0;j<n;j++){ 40 temp=(temp*(a[i]/i))%mod; 41 } 42 ans=(ans-mu[i]*temp+mod)%mod; 43 } 44 printf("Case #%d: %lld ",k,ans); 45 } 46 }
这里就是优化了相乘的过程,体会除法的截断过程

1 #include<bits/stdc++.h> 2 #define inf 0x3f3f3f3f 3 using namespace std; 4 typedef long long ll; 5 const int mod=1e9+7; 6 int mu[100005],a[100005]; 7 ll num[200005]; 8 int mm=100000; 9 void sieve(){ 10 mu[1]=1; 11 for(int i=1;i<=mm;i++){ 12 for(int j=2*i;j<=mm;j+=i){ 13 mu[j]-=mu[i]; 14 } 15 } 16 } 17 18 ll mod_pow(ll x,ll n,ll p){ 19 ll res=1; 20 while(n){ 21 if(n&1) res=res*x%p; 22 x=x*x%p; 23 n>>=1; 24 } 25 return res; 26 } 27 28 int main(){ 29 sieve(); 30 ll t,n,mi,ans; 31 //ios::sync_with_stdio(0); 32 scanf("%lld",&t); 33 for(int k=1;k<=t;k++){ 34 memset(num,0,sizeof num); 35 scanf("%lld",&n); 36 ans=0; 37 mi=inf; 38 for(int i=0;i<n;i++) {cin>>a[i];mi=min(mi,(ll)a[i]);num[a[i]]++;}//num中存的是个数,不是值 39 for(int i=1;i<=2*mm;i++) num[i]+=num[i-1];//num要设的大一些 40 for(int i=2;i<=mi;i++){ 41 ll temp=1; 42 for(int j=1;j*i<=mm;j++){ 43 temp=(temp*mod_pow(j,num[(j+1)*i-1]-num[j*i-1],mod))%mod; 44 } 45 ans=(ans-mu[i]*temp+mod)%mod; 46 } 47 printf("Case #%d: %lld ",k,ans); 48 } 49 }
最后一道签到题,不懂为什么+300就过了,+100,+200就WA,这里注意求坐标即可,固定两点,求另外两点
注意这里有一个性质,就是若坐标为整数点,则所构成的正多边形只有四边形。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 int a[605][605]; 5 struct node{ 6 int x; 7 int y; 8 }p[505]; 9 /*bool cmp(node &a,node &b){ 10 return a.x==b.x?a.y<b.y:a.x<b.x; 11 }*/ 12 int main(){ 13 int n,t1,t2,ans,x3,y3,x4,y4,x1,y1,x2,y2; 14 while(cin>>n){ 15 memset(a,0,sizeof a); 16 ans=0; 17 for(int i=0;i<n;i++){ 18 cin>>t1>>t2; 19 a[t1+300][t2+300]=1; 20 p[i].x=t1+300; 21 p[i].y=t2+300; 22 } 23 //sort(p,p+n,cmp); 24 for(int i=0;i<n;i++){ 25 for(int j=0;j<n;j++){ 26 if(i!=j){ 27 x1=p[i].x,y1=p[i].y; 28 x2=p[j].x,y2=p[j].y; 29 x3=x1+(y1-y2); y3= y1+x2-x1; 30 x4=x2+(y1-y2); y4= y2+x2-x1; 31 if(a[x3][y3]&&a[x4][y4]) ans++; 32 } 33 } 34 } 35 printf("%d ",ans/4); 36 } 37 return 0; 38 }
待补
