源自: https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
def qeval(x):
y = x**3
return x + y + 5
1 Flattening program => gates
只包含两种形式 x = y 和 x = y (op) z (where op can be +, -, *, / and y and z can be variables, numbers or themselves sub-expressions)
// 每一行可以理解为1个Gate
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5
2 Gates to R1CS
An R1CS is a sequence of groups of three vectors (a, b, c), and the solution to an R1CS is a vector s, where s must satisfy the equation s . a * s . b - s . c = 0
The length of each vector is equal to the total number of variables in the system
上面的例子中, 有6个变量 '~one', 'x', '~out', 'sym_1', 'y', 'sym_2'(~one和~out是必须的), 因此向量的长度为6
第一个gate对应的 (a,b,c)为
a = [0, 1, 0, 0, 0, 0] // x
b = [0, 1, 0, 0, 0, 0] // x
c = [0, 0, 0, 1, 0, 0] // sym_1
第二个gate对应的 (a,b,c) 为
a = [0, 0, 0, 1, 0, 0] // sym_1
b = [0, 1, 0, 0, 0, 0] // x
c = [0, 0, 0, 0, 1, 0] // y
第三个gate对应的为
a = [0, 1, 0, 0, 1, 0] // y + x
b = [1, 0, 0, 0, 0, 0] // ~one
c = [0, 0, 0, 0, 0, 1] // sym_2
第四个gate对应的为
a = [5, 0, 0, 0, 0, 1] // 5 * ~one + sym_2
b = [1, 0, 0, 0, 0, 0] // ~one
c = [0, 0, 1, 0, 0, 0] // ~out
同时满足这四个gate的(a,b,c)的s . a * s . b - s . c = 0的解 s 为
[1, 3, 35, 9, 27, 30]
将所有的a, b, c放到一起
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]
3 R1CS to QAP
QAP form: implements the exact same logic except using polynomials instead of dot products
多项式的阶取决于有多少gate, 这里有4个gate, 所以为3阶
A polynomials
[-5.0, 9.166, -5.0, 0.833] // 0.833 * x**3 — 5*x**2 + 9.166*x - 5, 经过(1,0) (2,0) (3,0) (4,5)这几个点
[8.0, -11.333, 5.0, -0.666] // 经过点 (1,1) (2,0) (3,1) (4,0)
[0.0, 0.0, 0.0, 0.0] // 经过点(1,0) (2,0) (3,0) (4,0) , 上面A的第三列
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166] // 经过点 (1,0) (2,0) (3,0) (4,1), 上面A的第6列
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
为什么要转成QAP
instead of checking the constraints in the R1CS individually, we can now check all of the constraints at the same time by doing the dot product check on the polynomials.
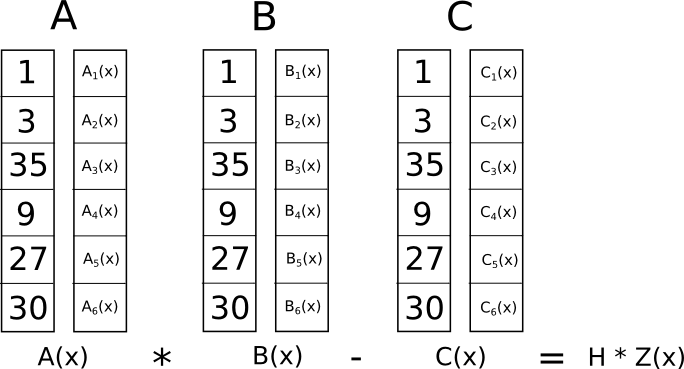
A(x) = A . s = [43.0, -73.333, 38.5, -5.166]
B(x) = B . s = [-3.0, 10.333, -5.0, 0.666]
C(x) = C . s = [-41.0, 71.666, -24.5, 2.833]
A . s * B . s — C . s:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]
Z = (x - 1) * (x - 2) * (x - 3) * (x - 4) (因为有4个gate)
Z = [24, -50, 35, -10, 1]
h = t / Z = [-3.666, 17.055, -3.444] // 因为t(1),t(2),t(3),t(4)都为0, 所以t(x)能够整除Z(x)
我们现在不用分别计算t(1), t(2), t(3), t(4)是否为0, 转而判断t(x)能否整除Z(x)
回顾:我们将R1CS的
s . a * s . b - s . c = 0的验证 转化为 判断QAP的t(x)在对应取值处(这里为1,2,3,4)是否为0, 然后再转化为t(x)能否整除Z(x)