mod补充:
1 = 12 mod 3
1 = 12 mod 4
1 = 12 mod 12(12=3*4)
但是这不是一定的,反例如下:
0 = 24 mod 12
0 = 24 mod 4
0 != 24 mod 48
1. set是无顺序无重复的集合,{}不等于{{}},因为后者包含一个元素
2. define sets
(1) 直接将元素枚举出来
(2)定义现有通用集合的子集
如指定元素必须满足的属性如x是自然数;
使用区间,如[1,5]={1,2,3,4,5}
派生整数集,如3z+1 = {3x+1:x∈Z}
(3)结合已经存在的集合
union(U)
intersection(∩)
complement 表示方法为A的c次方,x包含于全集,不包含于A
A and B are disjoint if A∩B = ∅
sest difference(A B) a but not b
symmetric difference(A⊕B) a and not b or b and not a, A⊕B = (AB)∪(B A)
X中元素个数表示为|X|,|Pow(x)|总是等于2的|x|次方
3. 子集S ⊆ T,包括T ⊆ T
真子集S ⊂ T,S ⊆ T and S 6= T
∅是任何集合的子集
正整数⊂N⊂Z⊂Q⊂R
!!!注意区分子集与元素的概念,a ∈{a,b}, a 不⊆{a,b}; {a}⊆{a,b}, {a} 不∈{a,b}
4. power set pow(x)={A:A⊆ X}
pow(∅)={∅}
pow(pow(∅))={∅,{∅}}
5. |AUB|=|A|+|B|-|A∩B|
|AUB|+|A∩B|=|A|+|B|
|AB|=|A|-|A∩B|
|A⊕B|=|AUB|-|A∩B|=|A+B|-2|A∩B|
6. formal language:empty word — λ
7. x*是由x中的0个或多个单词串联而成的一组单词
A = {aa,bb}, A∗ = {λ,aa,bb,aaaa,aabb,bbaa,bbbb,aaaaaa,...}
8.
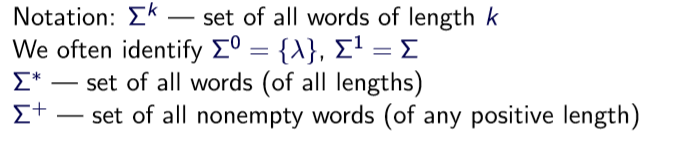
9. relation可以只选取sets中的一部分element,不需要做到一一对应
symmetric指使两边关系对称的relation,如等于和不等于,等号两边对调也是成立的;不symmetric的包括大于等于,小于等于等
同时relation也可以分为binary relation和congruence relation,上节课讲到的mod涉及到三个element,就属于congruence relation
10.


11. exercises中的A = {1,2}, B = {2,3}, C = {3,4}, X = [1,4],求 | on x做法是先做出所有可能的笛卡尔积,再从中找到符合条件的,本题中即可以被整除的,答案为{(1,1),(1,2),(1,3),(1,4),(2,2),(2,4),(3,3),(4,4))}
12. function中,左边的点均有relation可以对应
13. composition of functions

14. iterated(迭代):一个数的function仍是它本身,f o f, f o f o f, 也可以表示为f的二次方,f的三次方
15.

f;g means do f and then do g
16. a linear function compose itself can still get a linear function,如exercise中的g(n)=5n-11,g(g(n))=25n-66,也是线性的
17. Function is called surjective or onto if every element of the codomain is mapped to by at least one x in the domain
Im(f ) = Codom(f )
surjective的例子:floor,ceiling
错误例子f(x)=x^2
f : {a,...,e}∗ −→{a,...,e}∗只要a开头e结尾的都符合,所以不对
18. Function is called injective or 1–1 (one-to-one) if different x implies different f (x)
different input can get different output
!! Function is bijective if it is both surjective and injective.
19. 证明sets相同
a. 检查所有element
b. 证明a包含于b且b包含于a
c. 利用laws of set operators,如下图
