SDUST 2020/数据结构/期末集合.part2

接上

SDUST 2020/数据结构/期中集合.part1

---

04 队列

基本概念：

和栈相反，队列是一种先进先出的线性表，它只允许在表的一端进行插入，而在另一端删除元素。类似于日常生活中的排队问题，最早进入队列的人最早出队。

在队列中，允许插入的一端叫做表头，允许删除的一端称为队头。

在队列中，有两个指针，分别是front指针指向队首元素，rear指针指向对尾元素的后面，也就是待插入位置。

题目：

    1、在一个链队列中，front和rear分别为头指针和尾指针，则插入一个结点s的操作为（ ）。 C

          A.front=front->next    B.s->next=rear;rear=s    C.rear->next=s;rear=s;     D.s->next=front;front=s;、

    2、若用大小为6的数组来实现循环队列，且当前front和rear的值分别为0和4。当从队列中删除两个元素，再加入两个元素后，front和rear的值分别为多少？        D

               A.2和0    B.2和2     C.2和4    D.2和6

    3、如果循环队列用大小为m的数组表示，队头位置为front、队列元素个数为size，那么队尾元素位置rear为：D

                   A.front+size    B.front+size-1    C.(front+size)%m    D.(front+size-1)%m

    4、如果循环队列用大小为m的数组表示，且用队头指针front和队列元素个数size代替一般循环队列中的front和rear指针来表示队列的范围，那么这样的循环队列可以容纳的元素个数最多为：m

  队列的表示和实现

  1）链队列

       队列的链式存储，称为链队列。一个链队列显然需要两个分别指示队头(头指针)和队尾(尾指针)指针才能唯一确定

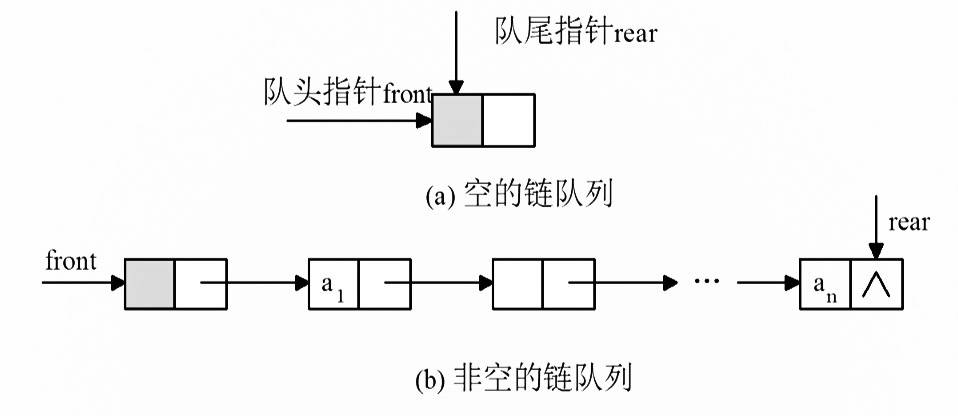
       定义如下：

typedef struct QNode
{
    QElemType data;//数据域
    struct QNode *next; //指针域
}Qnode,*QueuePtr;
typedef struct
{
    QueuePtr front;
    QueuePtr rear;
}LinkQueue;

 

    2）循环队列：队列的顺序表示和实现

       用一组连续的存储单元一次存放队列的元素，并设两个指针front、rear分别指示队头和队尾元素的位置

      front：指向实际的队头 ；rear：指向实际队尾的下一位置

      初态：front=rear=0 ；

      队空：front=rear ；

      队满：rear=M。

      入队：q[rear]=x ; rear=rear+1;

      出队：x=q[front] ; front=front+1;

      定义如下：

#define MAXSIZE 100 //队列最大长度
typedef struct
{
    QElemType element[MAXSIZE];
    int front;
    int rear;
}SeqQueue;

       假溢出的解决方法：

        ①将队中元素向队头移动

        ②采用循环队列；q[0]接在Q[M-1]之后

         初态：front=rear=0或M-1;

         队空：front=rear;

         入队：q[rear]=x ; rear=(rear+1)%M；

         出队：x=q[front] ; front=(front+1)%M；

         队满：留一个空间不用 (rear+1)%M=front

                    或者另设一个标志以区分队空队满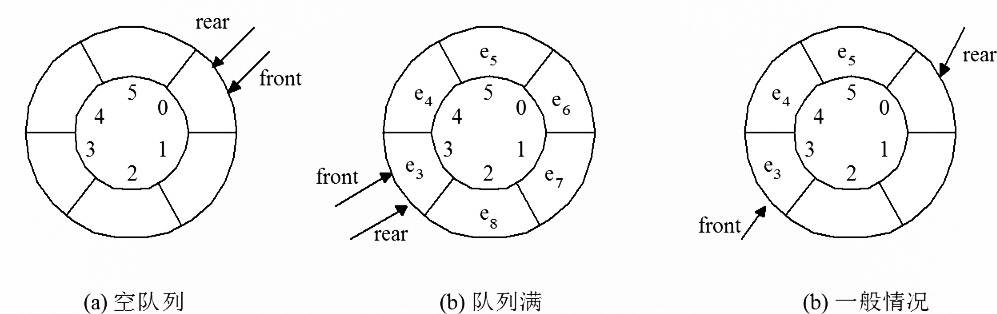

---

05 串

1应用：

①定位函数Index(S,T,pos)

     含义：若主串S中存在和串T相同的子串，则返回它在主串S中第pos个字符之后第一次出现的位置；否则函数值为0.

     算法基本思想为 StrCompare( SubString(S,i,StrLength(T)) , T ) = 0?

int Index(string s,string t,int pos)
{
    int m,n,i;
    if(pos>0)
    {
        n=strlen(s);
        m=strlen(t);
        i=pos;

        while(i<=n-m+1)
        {
            SubString(sub,S,i,m);  //取S串中i位置起，长度为m(T串长度)的串，保存在sub中。
            if(StrCompare(sub,t)!=0)
                i++;
            else
                return i
            }//while

    }//if
    return 0;
}

    ②kmp算法

         k-m-p

2串的存储表示：以串的联接算法为例

     ①定长存储表示

        特点：串的实际长度可在这个予定义长度的范围内随意设定，超过予定义长度的串值则被舍去，称之为"截断”。
                    按这种串的表示方法实现的串的运算时，其基本操作为“字符序列的复制”。

        串的联接算法中需分三种情况处理

     ②堆分配存储表示

         特点：系统利用函数malloc()和free()进行串值空间 的动态管理，为每一个新产生的串分配一个存储区，称串值共享的存储空间为“堆”

         算法：

Status Concat(HString &T，HString S1,HString S2)
{

    if(T.ch)
        free(T.ch);
    if(!(T.ch=(char*)malloc((S1.length+S2.length)*sizeof(char))))
        exit(OVERFLOW);

    T.ch[0..S1.length-1]=S1.[0..S1.length-1];
    T.length=S1.length+S2.length;
    T.ch[S1.length..T.length-1]=S2.ch[0..length-1];

    return OK;
}//Concat;

---

06 数组

数组的顺序表示和实现类型特点:
只有引用型操作，没有加工型操作；数组是多维的结构，而存储空间是一一个- -维的结构。
有两种顺序映象的方式：以行序为主序(低下标优先)、以列序为主序(高下标优先)。

稀疏矩阵：

    定义：假设m行n列的矩阵含有t个非零元素，则称  δ=t/(mxn)  为稀疏因子，通常认为δ<= 0.05的矩阵为稀疏矩阵

    随机稀疏矩阵的压缩存储方法：

      ①三元组顺序表：以矩阵的转置为例

        定义：

#define MAXSIZE 12500//非零元个数最大值
typedef struct
{
    int i,j;     //该非零元的行下标和列下标
    Elemtype e;  //该非零元的值
} Triple         //三元组类型
typedef union
{
    Triple data[MAXSIZE+1];//data[0]未用，所以要+1
    int mu,nu,tu;//行数、列数、非零元个数
} TSMatrix; //稀疏矩阵类型

        特点：非零元在表中按行序有序存储，便于进行依行顺序处理的矩阵运算

        算法：

Status TransposeSMatrix(TSMatrix M,TSMatrix &T)
{
        T.mu=M.nu;
        T.nu=M.mu;
        T.tu=M.tu;
        if(T.tu)
        {
            int q=1;
            for(int col=1;col<M.nu;col++)
                for(int p=1;p<M.tu;p++)
                  if(M.data[p].j==col)
            {
                T.data[q].i=M.data[p].j;
                T.data[q].j=M.data[p].i;
                T.data[q].e=M.data[p].e;
                q++;
            }
        }//if
        return OK;
}

      算法的优化：快速转置

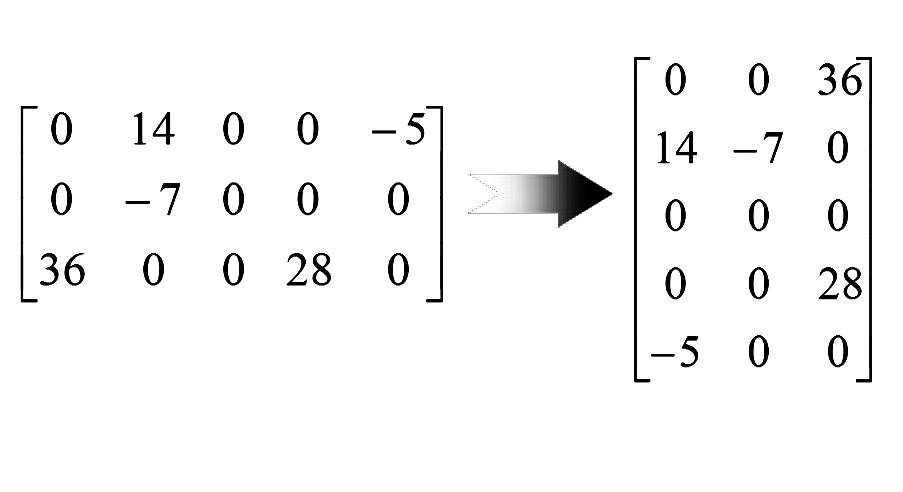
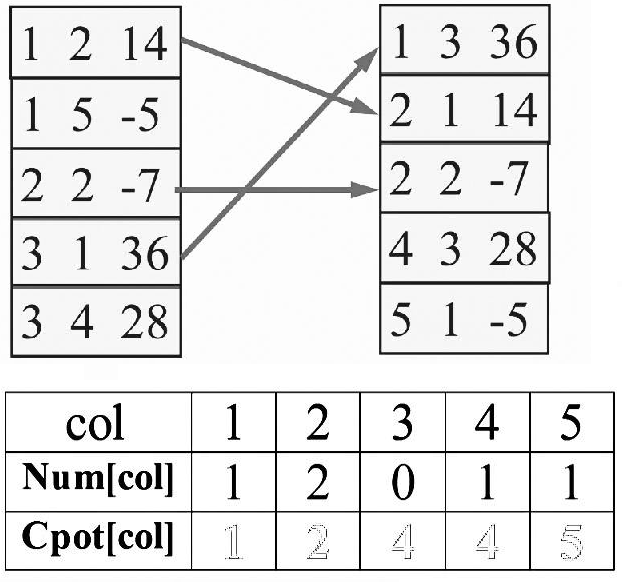
         上图为 原矩阵和新矩阵的三元组排序

         下图表格：num[col]：原矩阵第col列的非零元个数

                           cpot[col]：原矩阵第col列的第一个非零元在新矩阵中的位置

Status FastTransposeSMatrix(TSMatrix M,TSMatrix &T)
{
    T.mu=M.nu;
    T.nu=M.mu;
    T.tu=M.tu;

    if(T.tu)
    {
        for(col=1; col<M.nu; col++)
            num[col]=0;

        for(t=1; t<M.tu; t++)
            num[M.data[t].j]++;

        cpot[1]=1;
        for(col=2; col<=M.nu; col++)
            cpot[col]=cpot[col-1]+num[col-1];

        for(p=1; p<=M.tu; p++)
        {
            col=M.data[p].j;
            q=cpot[col];
            T.data[q].i=M.data[p].j;
            T.data[q].j=M.data[p].i;
            T.data[q].e=M.data[p].e;
            copt[col]++;
        }
    }//if
    return OK;
}//FastTransposeSMatrix

      非三元组法的矩阵转置：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int N,M;//行列
    scanf("%d %d",&N,&M);
    int i,j,a[N][M],b[M][N];

    for(i=0; i<N; i++)
    {
        for(j=0; j<M; j++)
        {
            scanf("%d",&a[i][j]);
        }
    }
    //输出矩阵a
    printf("Array a:
");
    for(i=0; i<N; i++)
    {
        for(j=0; j<M; j++)
        {
            printf("%5d",a[i][j]);
            b[j][i]=a[i][j];
        }
        printf("
");
    }
    //输出矩阵b
    printf("Array b:
");
    for(i=0; i<M; i++)
    {
        for(j=0; j<N; j++)
        {
            printf("%5d",b[i][j]);
        }
        printf("
");
    }

}

    ②行逻辑联接的顺序表：以矩阵相乘为例

          定义：

          增加了一个数据成员rpos，其值在稀疏矩阵的初始化函数中确定。

#define MAXMN 500
typedef struct
{
    Triple data[MAXSIZE+1];
    int rpots [MAXMN+1];
    int mu,nu,tu;
}RLSMatrix;

         特点：可以随机存取某一行的非零元

         算法：