一般情况,算法中基本操作重复的次数是关于 问题规模n 的某个函数f(n)(频度)
算法的时间量度记作T(n)=O(f(n)),即为时间复杂度。
简单来讲,计算时间复杂度,就是根据代码,将重复次数用一个含有 问题规模n 的代数式表示出来。
①O(1)
⭐ 如果算法的执行时间不随着问题规模n的增加而增长,即使算法中有上千条语句,其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。
eg. x=0;
for(i=0;i<1000;i++)
x+=i;
②O(n^a)
eg1. for(i=0;i<n;i++)
for(j=0;j<n;j++)
x+=1;
Σ(i=0—n)Σ(j=0—n)*1=n*n
eg2.if ( A > B )
{ for ( i=0; i<N*N/100; i++ )
for ( j=N*N; j>i; j-- )
A += B; }
else
{ for ( i=0; i<N*2; i++ )
for ( j=N*3; j>i; j-- )
A += B; }
选取需要时间最长的那个循环,显然是if里面的 n^5
、eg3.int func ( int n )
{ int i = 0, sum = 0;
while ( sum < n )
sum += ++i;
return i; }
③O(log an)
eg. for (int i = 1; i <= n; i *= c)
a = a + 1;
设频度f(n),则有 c^f(n)*1<=n,取等号时计算,得 f(n)=O(log cn)
同理,i执行 i/=c 的时候也是成立的:
for (int i = n; i > 0; i /= c) {
a = a + 1;}
④其它
eg.for(i=0; i<n; i++)
for(j=i; j>0; j/=2)
printf(“%d ”, j);
下列函数中,哪个函数具有最慢的增长速度:B
N^1.5 NlogN^2 N^2logN N(logN)^2
常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<…<Ο(2n)<Ο(n!)
另一种计算思想
for (i=1;i<n;i++)
{
y=y+1; ①
for (j=0;j<=(2*n);j++)
x++; ②
}
语句1的频度是n-1
语句2的频度是(n-1)*(2n+1)=2n2-n-1
则f(n)=2n2-n-1+(n-1)=2n2-2;
常用算法时间复杂度和空间复杂度
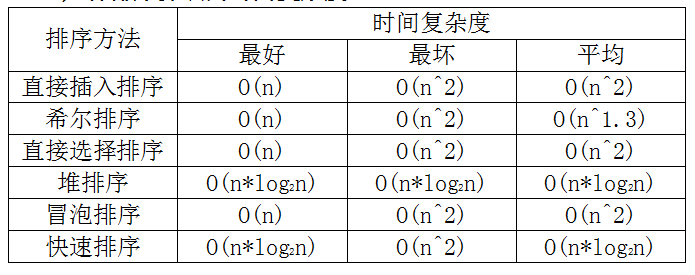
图源网络