回归模型是机器学习中很重要的一类模型,不同于常见的分类模型,回归模型的性能评价指标跟分类模型也相差很大,这里简单基于工作中的一点实践来记录一下基于sklearn库计算回归模型中常用的四大评价指标主要包括:explained_variance_score、mean_absolute_error、mean_squared_error、r2_score,详细的解释已经在代码注释中了,就不再多解释了,具体实践如下:
1、可解释方差(explained_variance_score)
解释回归模型的方差得分,其值取值范围是[0,1],越接近于1说明自变量越能解释因变量的方差变化,值越小则说明效果越差。

y_hat :预测值, y :真实值, var :方差
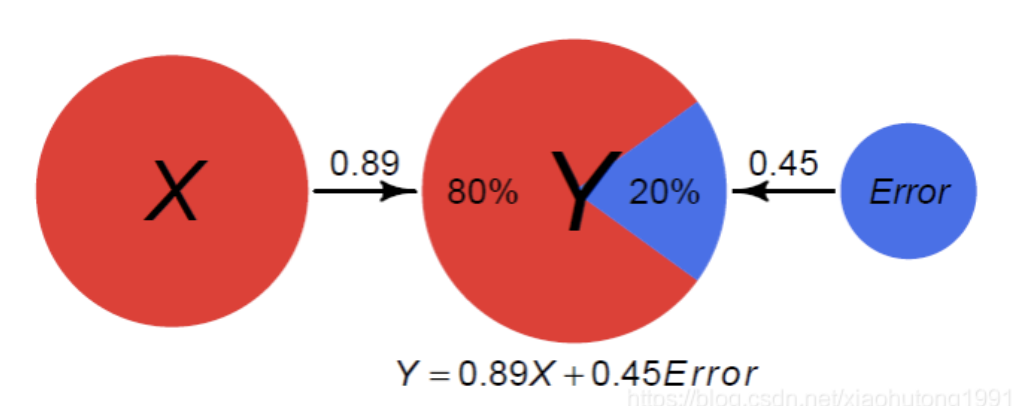
在理解“可解释方差”前,需要先了解下方差:离平均的平方距离的平均。方差很难理解,其中的一个原因是很难可视化。可解释方差并不意味着解释了方差,仅仅意味着我们可以使用一个或多个变量来比以前更准确地预测事物。在许多模型中,如果X与Y相关,X可以说是”解释”了Y中的方差,即使X并不真正导致Y。在下面的例子中,Y的方差的80%是由于X,剩下的20%由其他的一些Error导致的。由于X与Error非相关的z-score值,路径系数等于与Y的相关系数。
2、平均绝对误差(mean_absolute_error)
平均绝对误差(Mean Absolute Error,MAE),用于评估预测结果和真实数据集的接近程度的程度,其值越小说明拟合效果越好。平均绝对误差 (MAE)是最容易理解的回归误差指标。 我们将为每个数据点计算残差,只取每个残差的绝对值,以使负残差和正残差不会被抵消。 然后,我们取所有这些残差的平均值。 有效地,MAE描述了残差的典型大小。 MAE优缺点:虽然平均绝对误差能够获得一个评价值,但是你并不知道这个值代表模型拟合是优还是劣,只有通过对比才能达到效果。

3、均方误差(mean_squared_error)
均方差(Mean squared error,MSE),该指标计算的是拟合数据和原始数据对应样本点的误差的平方和的均值,其值越小说明拟合效果越好。由于MSE与我们的目标变量的量纲不一致,为了保证量纲一致性,我们需要对MSE进行开方,即均方根误差(RMSE):均方根误差 Root Mean Squared Error(RMSE)
均方根误差RMSE(root-mean-square error), 均方根误差亦称标准误差,它是观测值与真值偏差的平方与观测次数比值的平方根。均方根误差是用来衡量观测值同真值之间的偏差。标准误差对一组测量中的特大或特小误差反映非常敏感,所以,标准误差能够很好地反映出测量的精密度。可用标准误差作为评定这一测量过程精度的标准。
这不就是MSE开个根号么。有意义么?其实实质是一样的。只不过用于数据更好的描述。例如:要做房价预测,每平方是万元,我们预测结果也是万元。那么差值的平方单位应该是 千万级别的。那我们不太好描述自己做的模型效果。我们的模型误差是多少千万?于是干脆就开个根号就好了。我们误差的结果就跟我们数据是一个级别的,可在描述模型的时候就说,我们模型的误差是多少万元。
RMSE与MAE对比:RMSE相当于L2范数,MAE相当于L1范数。次数越高,计算结果就越与较大的值有关,而忽略较小的值,所以这就是为什么RMSE针对异常值更敏感的原因(即有一个预测值与真实值相差很大,那么RMSE就会很大)。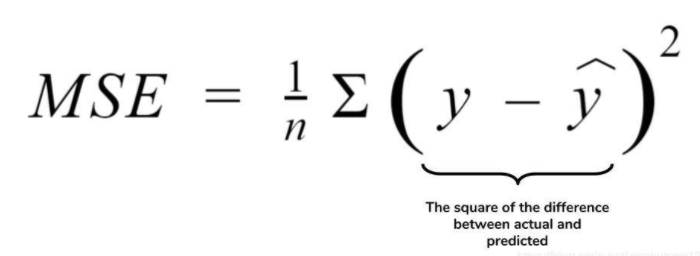
4、决定系数、R方(r2_score)
判定系数,其含义是也是解释回归模型的方差得分,其值取值范围是[0,1],越接近于1说明自变量越能解释因变量的方差变化,值越小则说明效果越差。又称为the coefficient of determination。判断的是预测模型和真实数据的拟合程度,最佳值为1,同时可为负值。如果结果是0,就说明我们的模型跟瞎猜差不多。如果结果是1。就说明我们模型无错误。如果结果是0-1之间的数,就是我们模型的好坏程度。如果结果是负数。说明我们的模型还不如瞎猜。
R方可以理解为因变量y中的变异性能能够被估计的多元回归方程解释的比例,它衡量各个自变量对因变量变动的解释程度,其取值在0与1之间,其值越接近1,则变量的解释程度就越高,其值越接近0,其解释程度就越弱。
一般来说,增加自变量的个数,回归平方和会增加,残差平方和会减少,所以R方会增大;反之,减少自变量的个数,回归平方和减少,残差平方和增加。为了消除自变量的数目的影响,引入了调整的R方。
![]()
Q:我知道r2_score表示的是在总变量中模型解释的百分比。但是explained_variance_score和它有什么区别?
从公式的差别角度看:当残差的均值为0时,它俩是一样的。至于用哪个,就看你有没有假设残差均值为0。

#!usr/bin/env python #encoding:utf-8 from __future__ import division ''' __Author__:沂水寒城 功能:计算回归分析模型中常用的四大评价指标 ''' from sklearn.metrics import explained_variance_score, mean_absolute_error, mean_squared_error, r2_score def calPerformance(y_true,y_pred): ''' 模型效果指标评估 y_true:真实的数据值 y_pred:回归模型预测的数据值 explained_variance_score:解释回归模型的方差得分,其值取值范围是[0,1],越接近于1说明自变量越能解释因变量 的方差变化,值越小则说明效果越差。 mean_absolute_error:平均绝对误差(Mean Absolute Error,MAE),用于评估预测结果和真实数据集的接近程度的程度 ,其其值越小说明拟合效果越好。 mean_squared_error:均方差(Mean squared error,MSE),该指标计算的是拟合数据和原始数据对应样本点的误差的 平方和的均值,其值越小说明拟合效果越好。 r2_score:判定系数,其含义是也是解释回归模型的方差得分,其值取值范围是[0,1],越接近于1说明自变量越能解释因 变量的方差变化,值越小则说明效果越差。 ''' model_metrics_name=[explained_variance_score, mean_absolute_error, mean_squared_error, r2_score] tmp_list=[] for one in model_metrics_name: tmp_score=one(y_true,y_pred) tmp_list.append(tmp_score) print ['explained_variance_score','mean_absolute_error','mean_squared_error','r2_score'] print tmp_list return tmp_list
结果如下:
['explained_variance_score', 'mean_absolute_error', 'mean_squared_error', 'r2_score']
[0.709825411300075, 4.719, 112.613, 0.6725361793319165]
参考文献: