机器学习算法学习

1. 线性回归

 

问题1：回归问题和分类问题。

回归(Y)和分类(Y)本质上都是通过一系列影响因子 (X) 系数 (权重w或 θ) 计算得出来的值，分类得出的是具体的某一类，所有可能值是离散的，回归得出的是一个值，所有可能值是连续的。回归一般公式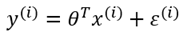：，误差是独立同分布且服从均值为0方差为的高斯分布

 

 

1. Logistic回归

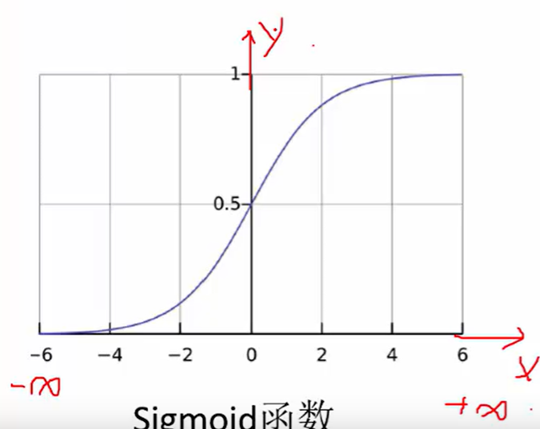
Logistic回归是一个经典的二分类问题，通过Sigmoid函数能够将结果映射到 [0, 1] 区间内，以0.5作为阈值分为两类。

Sigmoid函数将x的值映射到 [0, 1] 区间内

 

表达式：

 

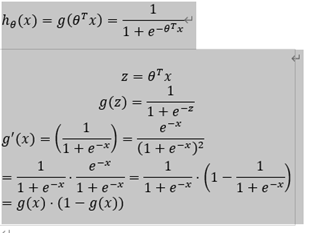
1. 梯度下降原理

为了能够找到更好的，就是尝试如何改变使其损失下降最快，很显然沿着梯度反方向下坡是最快的。

 

1. 模型评估方法

交叉验证

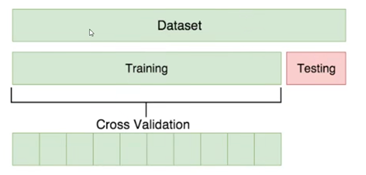
训练集划分：training：80%， testing：20%

Cross validation:将training划分为等10份，选取其中9份（不固定）训练，剩余一份进行验证。

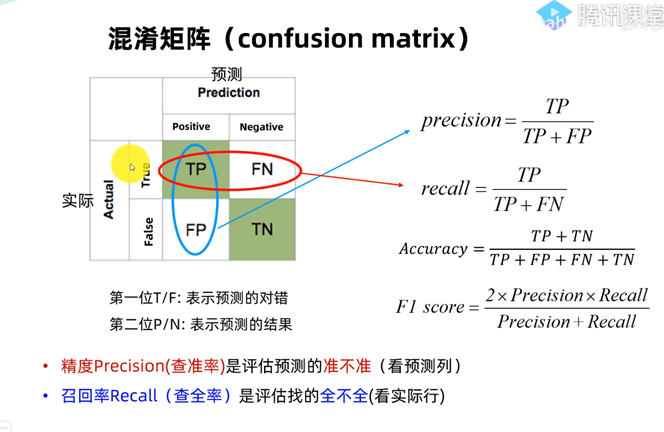
混淆矩阵

T=True; F=False

P=目标； N:非预测目标

TP:正确T->预测成目标P

FP: 错误F->预测成目标P

TN:正确T->预测成非目标N

FN:错误F->预测成非目标N

计算完混淆矩阵后，计算precision精确度和recall召回率

计算完precision和recall后计算F1 score更能体现出模型的优劣（精度和召回率中较低的值，影响最大）

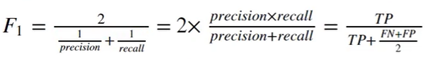
1. 聚类算法（图像领域可以应用于分割）

K-means算法

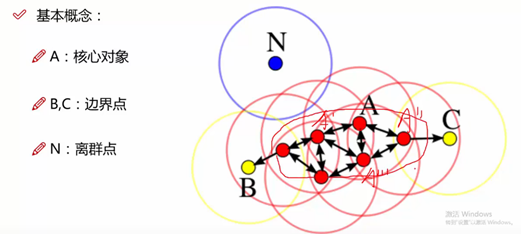
DBSCAN聚类算法（强大）

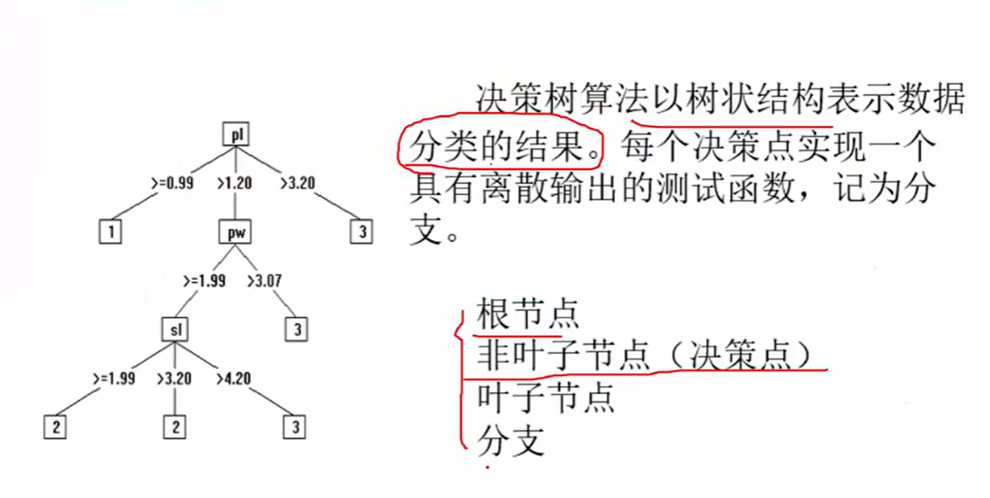
1. 决策树

既能够做分类而也可以做回归

熵：（不稳定性）

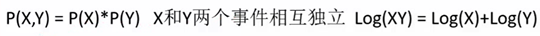
概率P越大的事情，熵（不确定性）越小，概率P越小的事情，熵（不确定性）越大。

首先构造决策树

谁来当根节点

 

 

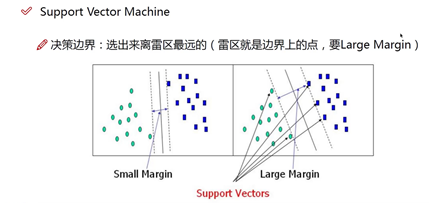
1. 支持向量机

要解决的问题：

1. 什么样的决策边界才是最好的？
2. 特征数据难分
3. 计算复杂度怎么样，能实际应用吗？

基于以上问题对SVM进行推导。

如果二维度不好分，那么变成三维度有可能就可以划分了。考虑实际问题，不能无限增加维度。

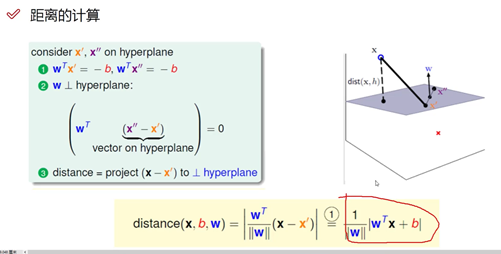
计算距离

假设x',x''都在平面上，计算x到平面的距离不好算。

先算出d = distance(x, x') # x到x'的距离，然后将d投影到平面法向量的角度，便计算出x到平面的距离。

现在需要找到平面法向量的方向=（法向量除以自身的模）

SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述：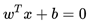

这里yi的值为正负1

 

1. 目标检测性能指标

引用：yolov5_哔哩哔哩_bilibili

检测

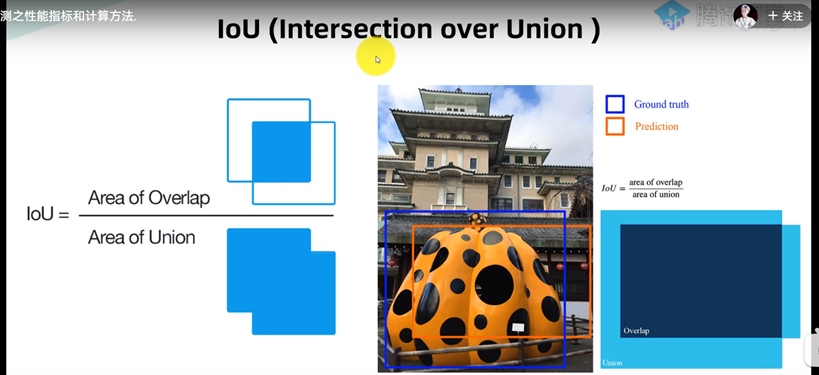
IoU

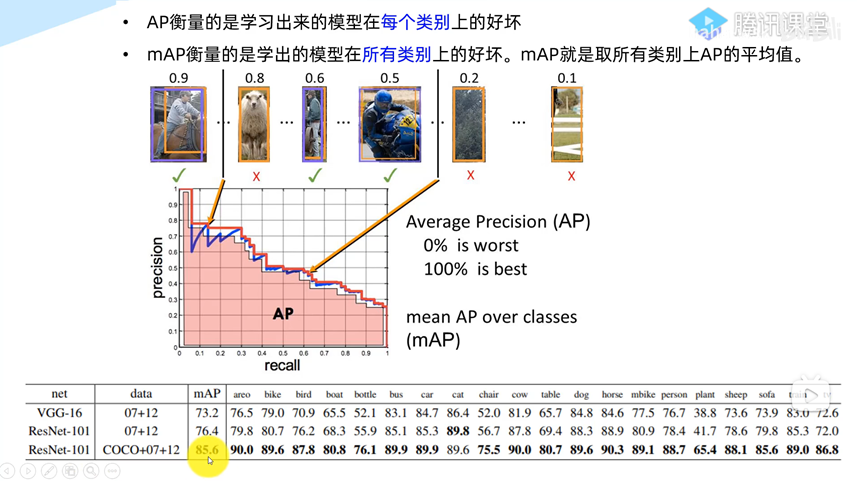
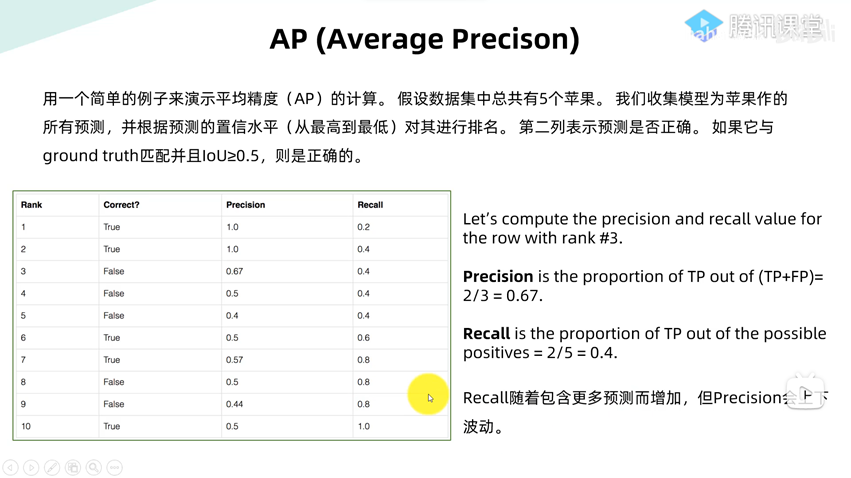
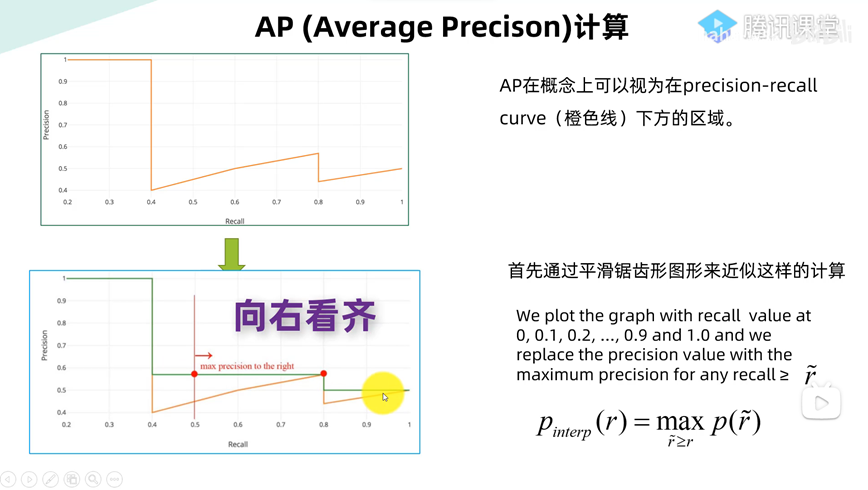
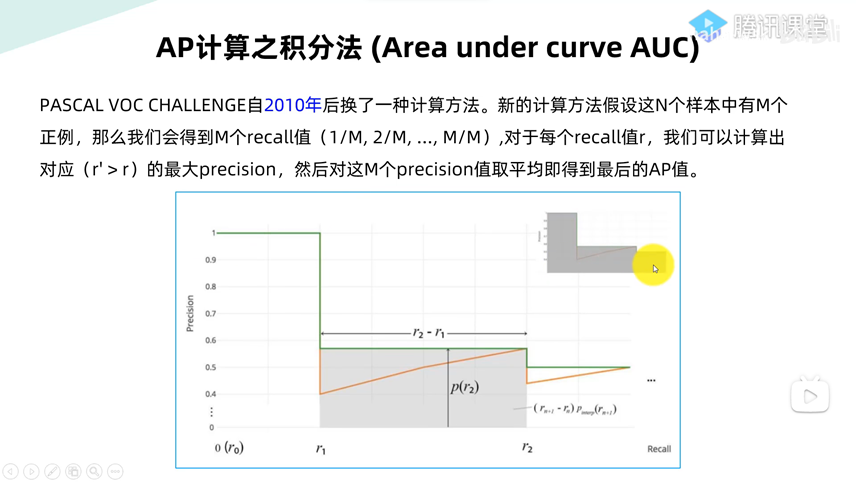
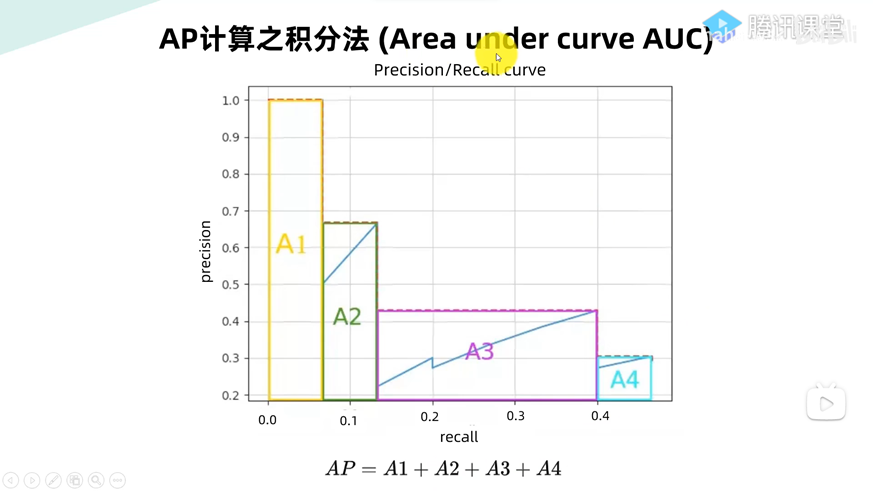
AP/mAP

 

 

 

 

 

 

 

 

 

 

 

 

检测速度（浮点运算量）

 

分类